2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ИЗОТЕРМИЧЕСКОЙ ФИЛЬТРАЦИИ ПЛАСТОВЫХ ФЛЮИДОВ

2.1. Вводные замечания

Характеристики фильтрационных потоков (давление, скорость фильтрации и др.) изменяются в пласте от точки к точке, т.е. образуют поле. Если элементы поля изменяются с течением времени, то движение флюидов является неустановившимся (нестационарным). Задачи неустановившейся фильтрации решаются методами математической физики с помощью систем дифференциальных уравнений.

Число уравнений в системе (дифференциальных и конечных) должно равняться числу неизвестных функций, характеризующих фильтрационный процесс и подлежащих определению. Такая система называется замкнутой.

В число дифференциальных уравнений фильтрации обязательно входят:

а) уравнение баланса массы в элементе пористой среды (уравнение неразрывности);

б) дифференциальные уравнения движения.

Для замыкания системы дополнительно вводятся уравнения состояния рассматриваемого флюида и пористой среды. Для получения решения системы уравнений задаются условия на границах пласта и в начальный момент времени.

В результате интегрирования прежде всего определяются распределение давления и скорости фильтрации по всему пласту в любой момент времени, т.е.

Р = Р (x,y,z,t) ,

V_x = V_x (x,y,z,t) ,

V_y = V_y (x,y,z,t) ,

V_z = V_z (x,y,z,t) .

В ряде случаев при постановке задачи жидкость и пласт можно считать несжимаемыми. Пористая среда считается несжимаемой (недеформируемой), если объем пор не изменяется при изменении давления в них жидкости. Если же изменением объема пор при изменении давления пренебречь нельзя, то такие среды следует рассматривать как упругие (деформируемые, сжимаемые).

При рассмотрении несжимаемой идеальной жидкости (,  - const) в недеформируемой пористой среде (К, m - const) число искомых функций ограничивается четырьмя перечисленными функциями.

Для фильтрации сжимаемого флюида в деформируемой (упругой) пористой среде нужно дополнительно определить плотность , вязкость , пористость m и проницаемость К как функции координат и времени. В этом случае нужно иметь восемь уравнений - дифференциальных и конечных - для определения восьми характеристик фильтрационного потока, жидкости и пористой среды.

Постановка математической задачи, соответствующей процессу разработки реальной залежи и включающей дифференциальные и конечные уравнения, а также начальные и граничные условия, является центральным этапом моделирования.

Аналитическое (в виде формул) решение системы дифференциальных уравнений можно получить лишь в ограниченном числе простейших, сильно идеализированных случаев. В более сложных случаях система решается численными методами с применением ЭВМ.

2.2. Вывод уравнения неразрывности фильтрационного потока для однородного сжимаемого флюида в деформируемой пористой среде

Для вывода дифференциальных уравнений фильтрации в пористой среде выделяется бесконечно малый элемент пористой среды и затем рассматриваются изменения массы, энергии и т.д., происходящие в нем за бесконечно малый промежуток времени. При этом используются законы сохранения массы и энергии, а также дополнительные результаты, полученные в ходе экспериментального изучения свойств среды и поведения в ней флюидов.

Мы ограничимся рассмотрением процессов, для которых температура флюида равна температуре среды и неизменна. Вследствие того, что фильтрация представляет собой очень медленный процесс, изменение температуры, возникающее в ходе движения за счет сопротивления и расширения вещества, успевает компенсироваться теплообменом с окружающими горными породами.

Для таких изотермических процессов уравнения энергии рассматривать уже не нужно. Вместе с тем изучение неизотермических процессов имеет особо важное значение в связи с возможностью повышения нефтеотдачи при закачке в пласт теплоносителя (горячей воды, пара).

Уравнение неразрывности (сплошности) фильтрационного потока представляет собой уравнение баланса массы в элементарном объеме пористой среды.

Выделим мысленно в пористой среде, в которой происходит движение флюида, элементарный объем в виде параллелепипеда с ребрами dx, dy, dz.

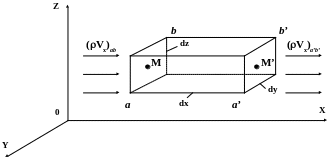
Пусть точка М, совпадающая с центром левой грани ав, имеет координаты x, y, z. Тогда точка М’ в центре грани а’b’ имеет координаты x+dx, y, z.

Масса флюида, втекающего в объем через грань ав за малый промежуток времени dt, записывается в виде:

(V_x)_abdydzdt .

Масса флюида, вытекающего из объема через грань а’в’ за малый промежуток времени dt, записывается в виде:

(V_x)_a’b’dydzdt .

Но так как при переходе от точки М к точке М’ координата x изменилась на малую величину dx, то можно записать:

.

Тогда изменение массы флюида в объеме abb’a’ за промежуток времени dt за счет потока вдоль оси x составит:

.

Аналогично выражения для изменения массы в элементарном объеме за счет потока вдоль осей y и z запишутся в виде:

и

.

Общее изменение (накопление) массы в объеме dxdydz за время dt будет равно:

. (2.1)

С другой стороны, масса флюида, находящегося в в рассматриваемом элементарном поровом объеме, равна:

,

где m – коэффициент пористости.

Тогда изменение массы М флюида за промежуток времени dt запишется в следующем виде:

. (2.2)

Приравнивая правые части выражений (2.1) и (2.2) и сокращая их на dxdydzdt, получим искомое уравнение неразрывности:

. (2.3)

Выражение в левой части уравнения (2.3) представляет собой дивергенцию вектора массовой скорости фильтрации, поэтому уравнение неразрывности имеет также следующую запись:

.

В случае установившейся фильтрации несжимаемой жидкости в недеформируемом пласте V=const, =const, m=const в каждой точке среды.

Тогда

,

в силу чего уравнение неразрывности принимает вид:

. (2.3’)