Шпоры по Электричеству и магнетизму / Новая папка (3) / Физика / 20

20. Закон Джоуля-Ленца. (Иродов стр. 132-135)

В основу решения задачи нахождения кол-ва теплоты, выделяющегося на определенном участке цепи за ед. времени, при прохождении через него тока, мы возьмем закон сохранения энергии и закон Ома.

Однородный участок цепи. Пусть интересующий нас участок заключен между сечениями 1 и 2 проводника. Найдем работу, которую совершают силы поля над носителями тока на участке 12 за время dt.

Е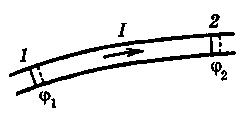сли сила тока в проводнике равна I, то за время dt через каждое сечение проводника пройдет заряд dq = Idt. В частности, такой заряд dq войдет внутрь участка через сечение 1 и такой же заряд выйдет из этого участка через сечение 2. Так как распределение зарядов в проводнике остается при этом неизменным (ток постоянный), то весь процесс эквивалентен непосредственному переносу заряда dq от се­чения 1 к сечению 2, имеющих потенциалы и .

Поэтому совершаемая при таком переносе работа сил поля

Согласно закону сохранения энергии элементарная ра­бота , где — теплота, выделяемая в единицу времени (тепловая мощность). Из сравнения последнего равенства с предыдущим получаем По закону Ома , то – закон Джоуля—Ленца (диф. форма).

Получим выражение закона в локальной форме, характеризующей выделение теплоты в различных местах проводящей среды. Выделим в данной среде элементарный объем в виде цилиндрика с образующими, параллельными вектору j — плотности тока в данном месте. Поперечное сечение цилиндрика , а его длина dl. Тогда на основании закона Джоуля-Ленца в этом объеме за время dt выделяется количество теплоты , где — объем цилиндрика. Разделив урав­нение на , получим удельную тепловую мощность тока: . Эта формула выражает закон Джоуля-Ленца в локальной форме: удельная тепловая мощность тока пропорциональ­на квадрату плотности электрического тока и удельному сопротивлению среды в данной точке.

Уравнение представляет собой наиболее общую форму закона Джоуля-Ленца, применимую к любым проводникам вне зависимости от их формы, однородности и от природы сил, возбуждающих электрический ток. Если на носители тока дей­ствуют только электрические силы, то на основании закона Ома :

Неоднородный участок цепи. Если участок цепи содержит источник э.д.с., то на носители тока будут действовать не только электрические силы, но и сторонние. В этом случае выделяемое в неподвижном проводнике тепло будет равно по закону сохранения энергии алгебраической сумме работ электрических и сторонних сил. Это же относится и к соответствующим мощностям: тепловая мощность должна быть равна алгебраической сумме мощностей электрических и сторонних сил. Проще всего в этом можно убедиться, умножив выражение на :

Слева – тепловая мощность . Последнее слагаемое справа – собой мощность, развиваемую сторонними силами на данном участке. Величина () изменяет знак при изменении направления тока .

Таким образом, уравнение означает, что тепловая мощность, выделяемая на участке цепи между точками 1 и 2, равна алгебраической сумме мощностей электрических и сторонних сил. Сумму этих мощностей, т.е. правую часть, называют мощностью тока на рассматриваемом участке цепи. Тогда можно сказать, что в случае неподвижного участка цепи мощность выделяемой на этом участке теплоты равна мощности тока.

Применив ко всей неразветвленной цепи (тогда ), получим , т.е. общее количество выделяемой за единицу времени во всей цепи джоулевой теплоты равно мощности только сторонних сил. Значит, теплота производится только сторонними силами. Роль же электрического поля сводится к тому, что оно перерас­пределяет эту теплоту по различным участкам цепи.

Получим теперь уравнение в локальной форме. Для этого умножим обе части уравнения на , а также учтем, что и . Тогда удельная тепловая мощность тока в неоднородной проводящей среде .