Пружинный маятник. Энергия маятника.
Пружинный маятник — механическая система, состоящая из абсолютно упругой пружины с коэффициентом упругости (жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m. Груз совершает гармонические колебания под действием упругой силы F=-kx.
Когда на массивное тело действует упругая сила, возвращающая его в положение равновесия, оно совершает колебания около этого положения. Такое тело называют пружинным маятником. Колебания возникают под действием внешней силы. Колебания, которые продолжаются после того, как внешняя сила перестала действовать, называют свободными. Колебания, обусловленные действием внешней силы, называют вынужденными. При этом сама сила называется вынуждающей.
В простейшем случае пружинный маятник представляет собой движущееся по горизонтальной плоскости твердое тело, прикрепленное пружиной к стене.
Второй закон Ньютона для такой системы при условии отсутствия внешних сил и сил трения имеет вид:
Если на систему оказывают влияние внешние силы, то уравнение колебаний перепишется так:
,
где f(x) — это равнодействующая внешних
сил соотнесённая к единице массы груза.
В случае наличия затухания, пропорционального скорости колебаний с коэффициентом c:
Потенциальная и кинетическая энергии тела даются выражениями
, .
Подставляем сюда зависимость от времени и получаем
, .
Учитывая формулу для частоты, получаем
.
То есть механическая энергия в этом случае сохраняется.
Физический маятник.
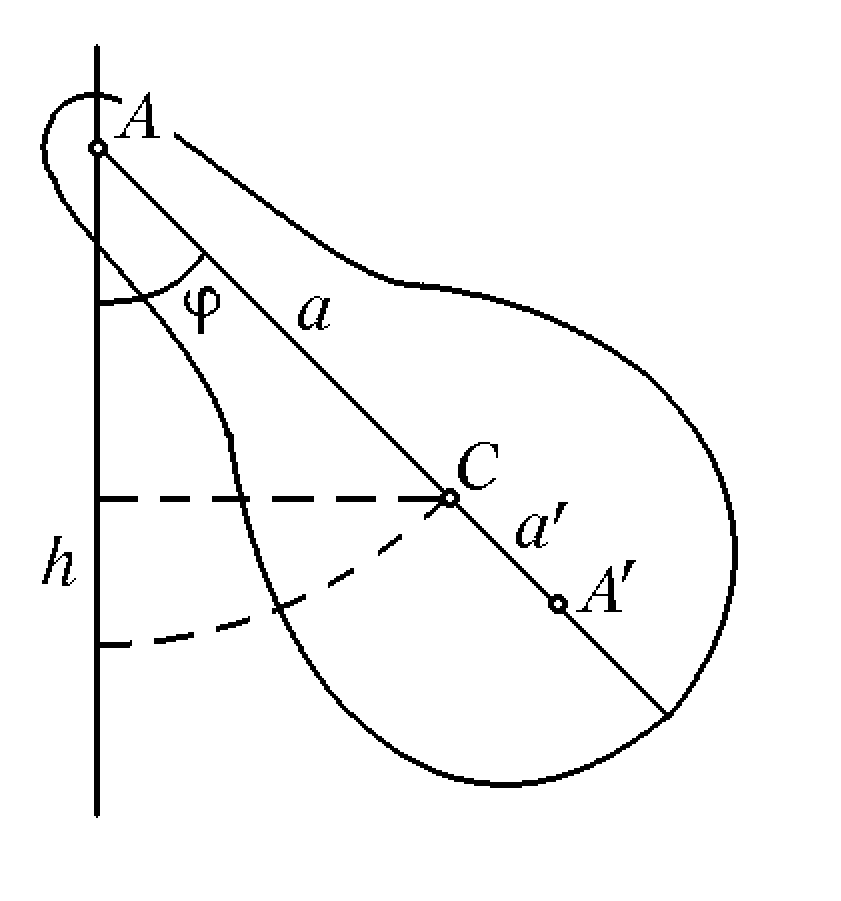
Физическим
маятником
называется твердое тело, совершающие
под действием силы тяжести колебания
вокруг неподвижной оси. Точка
пересечения
ее с вертикальной плоскостью, проходящей
через центр масс маятника, называется
точкой подвеса маятника. Положение тела
в каждый момент времени можно
характеризовать углом отклонения его
из положения равновесия
.
Момент силы тяжести
,
приложенной к центру масс
выражается
формулой
,
где
расстояние
от центра масс до точки подвеса. Уравнение
вращательного движения маятника выглядит
так
,
где
—
момент инерции маятника относительно
оси
.
Правая часть уравнения нелинейна
относительна угла
и
решать его трудно. Однако, если угол мал
,
то
и
мы получаем уравнение гармонического
колебания величины
.
Отсюда частота колебаний физического маятника равна
и период
Частным
случаем физического маятника является
математический маятник. Тогда
,
,
где
—
длина маятника и период равен
.
О
Л
Л
Макроскопическая система большого количества молекул. Ее параметры. Равновесная система.
Термодинамика — раздел физики, в котором изучаются общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, и процессы перехода между этими состояниями.
Термодинамической системой — совокупностью макроскопических тел, которые взаимодействуют и обмениваются энергией как между собой, так и с другими телами (внешней средой).
Термодинамические параметры (параметры состояния) — совокупность физических величин, характеризующих свойства термодинамической системы. Обычно в качестве параметров состояния выбирают температуру, давление и удельный объем.
Макроскопическая система находится в термодинамическом равновесии, если ее состояние с течением времени не меняется (предполагается, что внешние условия рассматриваемой системы при этом не изменяются).