18. Анализ сложных цепей постоянного тока при помощи законов Кирхгофа.

Для формулировки законов Кирхгофа, в электрической цепи выделяются узлы — точки соединения трёх и более проводников и контуры — замкнутые пути из проводников. При этом каждый проводник может входить в несколько контуров.

В этом случае законы формулируются следующим образом.

Первый закон (ЗТК, Закон токов Кирхгофа) гласит, что алгебраическая сумма токов в любом узле любой цепи равна нулю (значения вытекающих токов берутся с обратным знаком):

.

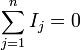Иными словами, сколько тока втекает в узел, столько из него и вытекает. Данный закон следует из закона сохранения заряда. Если цепь содержит p узлов, то она описывается p − 1 уравнениями токов. Этот закон может применяться и для других физических явлений (к примеру, водяные трубы), где есть закон сохранения величины и поток этой величины.

Второй закон (ЗНК, Закон напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений по любому замкнутому контуру цепи равна алгебраической сумме ЭДС, действующих вдоль этого же контура. Если в контуре нет ЭДС, то суммарное падение напряжений равно нулю:

для постоянных напряжений ;

19. Работа постоянной силы на прямолинейном перемещении

Определим работу для случая, когда действующая сила постоянна по величине и направлению, а точка ее приложения перемещается по прямолинейной траектории.

Работа W постоянной силы при прямолинейном движении точки ее приложения равна произведению модуля силы F на рас­стояние s и на косинус угла между направлением силы и направле­нием перемещения, т. е.

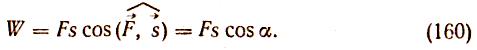
Угол α между направлением силы и направлением движения может меняться в пределах от 0 до 180°. При α < 90° работа положительна, при α > 90° — отрицательна, при α = 90° работа равна нулю.

Если сила составляет с направлением движения острый угол, она называется движущей силой, работа силы всегда положительна. Если угол между направлениями силы и перемещения тупой, сила оказывает сопротивление движению, совершает отрицательную работу и носит название силы сопротивления. Примерами сил сопротивления могут служить силы резания, трения, сопротивле­ния воздуха и другие, которые всегда направлены в сторону, про­тивоположную движению.

Когда α = 0°, т. е. когда направление силы совпадает с направлением скорости, тогда W = F s, так как cos 0° = 1. Произведение F cos α есть проекция силы на направление движения материальной точки. Следовательно, работу силы можно определить как произведение перемещения s и проекции силы на направление движения точки.

За единицу работы в Международной системе единиц (СИ) принят джоуль (Дж), равный работе силы в один ньютон (Н) на совпадающем с ней по направлению движения длиной в один метр:

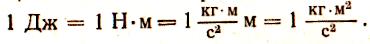
Применяется также более крупная единица работы — килоджоуль (кДж), 1 кДж = 1000 Дж = 10³ Дж. В технической системе (МКГСС) за единицу работы принят килограмм-сила метр (кгс^.м).

20. Понятие о срезе и смятии, Условия прочности

Срезом или сдвигом называется деформация, возникающая под действием двух близко расположенных противоположно направленных равных сил. При этом возникают

касательные напряжения. Частный случай среза — скалывание волокнистых материалов, в частности древесины, по плоскостям, параллельным волокнам.

При большом давлении может произойти значительное смятие стенок отверстия или стержня заклепки по поверхности их соприкосновения. В шпоночном соединении смятие может произойти по площади контакта вала или шкива со шпонкой.

Смятием называется местная деформация сжатия по площадкам передачи давления. Возникающие нормальные напряжения смятия являются местными; величина их быстро убывает при удалении от площадки соприкосновения элементов.

Условие прочности элементов, работающих на срез, имеет вид

где A_ср—площадь среза; [т_ср] —допускаемое касательное напряжение.

Величину допускаемого напряжения назначают на основании испытаний на срез. Обычно принимают [т_ср] = (0,70-0,80) [σ].

Проверку элементов конструкции на смятие производят по формуле

где A_см — площадь смятия; [σ_см] — допускаемое напряжение на смятие.

Обычно принимают [σ_см] = (1,7-2,2) [σ_см].

21. Емкостный элемент схем замещения цепей с изменяющимся током.

22.

23.

24.

25. Представление синусоидальных ЭДС, напряжений и токов.

Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами. Значения аргументов синусоидальных функций  и  называются фазами синусоид, а значение фазы в начальный момент времени (t=0):  и  - начальной фазой ( ). Величину , характеризующую скорость изменения фазового угла, называют угловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на  рад., то угловая частота есть , где f– частота. При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз. Для синусоидальных ЭДС е₁ и е₂ угол сдвига фаз:

.