Шпоры по Электричеству и магнетизму / Новая папка (3) / Физика / 21

21. Циркуляция индукции магнитного поля.

Теорема о циркуляции вектора (для магнитного поля по­стоянных токов в вакууме). Циркуляция вектора по произ­вольному контуру Г равна произведению на алгебраиче­скую сумму токов, охватываемых контуром Г:

(1)

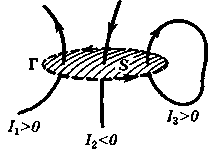где , причем — величины алгебраические. Ток счита­ется положительным, если его направление связано с направле­нием обхода по контуру правилом пра­вого винта. Ток противоположного на­правления считается отрицательным. Это правило иллюстрирует рисунке: здесь токи и положительные, ибо их направления связаны с направлением обхода по контуру правилом правого винта, а ток — отрицательный.

Теорема о циркуляции (1) может быть доказана исходя из закона Био-Савара. В общем случае произвольных токов это доказательство достаточно кропотливо, и мы не будем приво­дить его здесь. Мы будем рассматривать утверждение (1) как постулат, подтвержденный экспериментально.

Еще одно замечание. Если ток в (1) распределен по объ­ему, где расположен контур Г, то его можно представить как

Интеграл здесь берется по произвольной поверхности S, натя­нутой на контур Г. Плотность тока под интегралом соответству­ет точке, где расположена площадка , причем вектор обра­зует с направлением обхода по контуру правовинтовую систему.

Итак, в общем случае уравнение (1) можно записать так:

Тот факт, что циркуляция вектора , вообще говоря, не рав­на нулю, означает, что поле не потенциально (в отличие от электростатического поля). Такое поле называют вихревым или соленоидальным.

Так как циркуляция вектора пропорциональна току , ох­ватываемому контуром, то магнитному полю, в общем случае, нельзя приписать скалярный потенциал, который был бы свя­зан с вектором соотношением, аналогичным . Этот потенциал был бы неоднозначным: при каждом обходе по кон­туру и возвращении в исходную точку он получал бы прираще­ние, равное . Впрочем, в той области пространства, где токов нет, магнитный потенциал вводят и достаточно эффективно используют.