Шпоры по Электричеству и магнетизму / Новая папка (3) / Физика / !full

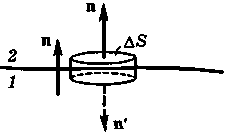
32. (1 из 2) Условия на границе двух магнетиков.

32. (2 из 2) Условия на границе двух магнетиков.

Речь идет об условиях для векторов и на границе разде­ла двух однородных магнетиков. Эти условия, как и в случае диэлектрика, мы получим с помощью теоремы Гаусса и теоре­мы о циркуляции. Для векторов и эти теоремы, напомним, имеют вид

Условие для вектора . Представим себе очень малой высоты цилиндрик, расположенный на границе раздела магнетиков, как показано на рисунке. Тогда поток вектора наружу из этого цилиндрика (потоком через боковую поверхность пренебрегаем) можно за­писать так:

Взяв обе проекции вектора на общую нормаль , получим , и предыдущее уравнение после сокращения на примет следующий вид:

т. е. нормальная составляющая вектора оказывается одина­ковой по обе стороны границы раздела. Эта величина скачка не испытывает.

Условия для вектора . Для большей общности будем пред­полагать, что вдоль поверхности раздела магнетиков течет по­верхностный ток проводимости с линейной плотностью . При­меним теорему о циркуляции вектора к очень малому прямо­угольному контуру, высота которого пренебрежимо мала по сравнению с его длиной , расположив этот контур так, как показано на рисунке. Пренебрегая вкла­дом в циркуляцию на боковых сторо­нах контура,

запишем для всего кон­ тура:

где — проекция вектора на нормаль к контуру (вектор образует с направлением обхода по контуру правовинтовую сис­тему). Взяв обе проекции вектора на общий орт касательной (в среде 2), получим , и после сокращения на пре­дыдущее уравнение примет вид

т. е. тангенциальная составляющая вектора , вообще говоря, при переходе границы раздела магнетиков претерпевает ска­чок, связанный с наличием поверхностных токов проводимо­сти.

Однако если на границе раздела магнетиков токов проводи­мости нет (), то тангенциальная составляющая вектора оказывается одинаковой по обе стороны границы раздела:

Итак, если на границе раздела двух однородных магнетиков тока проводимости нет, то при переходе этой границы состав­ляющие и изменяются непрерывно, без скачка. Составля­ющие же и при этом претерпевают скачок.

33. (1 из 1) Связь магнитного и механического моментов.

34. (1 из 1) Эдс индукции.

- уравнение магнитного момента

- более общее уравнение (на лекциях просто так дали)

(1)

Механический момент: (2)

Сравнивая (1) и (2) получаем :

ИЛИ

Найдем магнитный момент:

Найдем механический момент:

(знак минус из-за того моменты направлены в разные стороны)

Следовательно:

Открытие Фарадея. В 1831 г. Фарадеем было сделано одно из наиболее фундаментальных открытий в электродинамике — явление электромагнитной индукции. Оно заключается в том, что в замкнутом проводящем контуре при изменении магнитного потока (т. е. потока вектора В), охватываемого этим контуром, возникает электрический ток — его назва­ли индукционным.

Закон электромагнитной индукции. Согласно этому закону, какова бы ни была причина изменения магнитного потока, ох­ватываемого замкнутым проводящим контуром, возникающая в контуре э.д.с. индукции" определяется формулой

Знак минус в этом уравнении связан с определенным прави­лом знаков. Знак магнитного потока Ф связан с выбором нор­мали к поверхности S, ограниченной рассматриваемым конту­ром, а знак э.д.с. индукции — с выбором положительного на­правления обхода по контуру.

Здесь предполагается (как и ранее), что направление норма­ли к поверхности S и положительное направле­ние обхода контура связаны друг с другом прави­лом правого винта (рисунок). Поэтому, выбирая (произвольно) направление нормали, мы опреде­ляем как знак потока Ф, так и знак (а значит, и «направление») э.д.с. индукции

При сделанном нами выборе положительных направле­ний — в соответствии с правилом правого винта — величины и имеют противоположные знаки.

Единицей магнитного потока является вебер (Вб). При ско­рости изменения магнитного потока 1 Вб/с в контуре индуци­руется э.д.с., равная 1 В.

35. (1 из 2) Свойства взаимной индукции.

35. (2 из 2) Свойства взаимной индукции.

Взаимная индуктивность. Рассмот­рим два неподвижных контура 1 и 2 (рисунок), расположенные достаточно близко друг к другу. Если в контуре 1 течет ток , он создает через контур 2 полный магнитный поток Ф₂, пропор­циональный (при отсутствии ферромаг­нетиков) току :

Совершенно так же, если в контуре 2 течет ток , он создает через контур 1 полный магнитный поток

Коэффициенты пропорциональности и называют вза­имной индуктивностью контуров. Очевидно, взаимная ин­дуктивность численно равна магнитному потоку сквозь один из контуров, создаваемому единичным током в другом контуре. Коэффициенты и зависят от формы, размеров и взаим­ного расположения контуров, а также от магнитной проницае­мости окружающей контуры среды. Выражаются эти коэффи­циенты в тех же единицах, что и индуктивность .

Теорема взаимности. Соответствующий расчет дает (и опыт его подтверждает), что при отсутствии ферромагнетиков коэф­фициенты и одинаковы:

Это замечательное свойство взаимной индуктивности приня­то называть теоремой взаимности. Благодаря этой теореме можно не делать различия между и и просто говорить о взаимной индуктивности двух контуров.

Смысл равенства в том, что в любом случае магнит­ный поток сквозь контур 1, созданный током в контуре 2, равен магнитному потоку сквозь контур 2, созданному та­ким же током в контуре 1. Это обстоятельство нередко позволяет сильно упрощать решение вопроса о

нахождении, напри­мер, магнитных потоков. Вот два примера.

Взаимная индукция. Наличие магнитной связи между кон­турами проявляется в том, что при всяком изменении тока в одном из контуров в другом контуре возникает э.д.с. индукции. Это явление и называют взаимной индукцией.

Согласно закону электромагнитной индукции э.д.с., возни­кающие в контурах 1 и. 2, равны соответственно:

,

Здесь предполагается, что контуры неподвижны и ферромаг­нетиков поблизости нет.

С учетом явления самоиндукции ток, например, в контуре 1 при изменении токов в обоих контурах определяется по закону

Ома как

где — сторонняя э.д.с. в контуре 1 (помимо индукционных э.д.с.). — индуктивность контура 1. Аналогичное уравнение можно записать и для определения силы тока 1₂ в контуре 2.

Отметим, что на явлении взаимной индукции основано дей­ствие трансформаторов — устройств, служащих для преобразо­вания токов и напряжений.

36. (1 из 1) Эдс самоиндукции.

37. (1 из 2) Плотность энергии магнитного поля.

При изменении силы тока в контуре согласно возникает э.д.с. самоиндукции :

Если при изменении тока индуктивность L остается посто­янной (не меняется конфигурация контура и нет ферромагне­тиков), то

Здесь знак минус показывает, что всегда направлена так, чтобы препятствовать изменению силы тока — в соответствии с правилом Ленца. Эта э.д.с. стремится сохранить ток неизмен­ным: она противодействует току, когда он увеличивается, и поддерживает ток, когда он уменьшается. В явлениях самоин­дукции ток обладает «инерцией», потому что эффекты индук­ции стремятся сохранить магнитный поток постоянным, точно так же, как механическая инерция стремится сохранить ско­рость тела неизменной.

Формула (1) выражает магнит­ную энергию тока через индуктивность и ток (при отсутствии ферромагнетиков). Однако и здесь, как и в случае электриче­ской энергии заряженных тел, энергию можно выразить непо­средственно через магнитную индукцию . Убедимся, что это так сначала на простейшем примере длинного соленоида, пре­небрегая искажением поля на его торцах (краевыми эффекта­ми). Подстановка в формулу (1) выражения дает

А так как , то (2)

Эта формула справедлива для однородного поля, заполняю­щего объем V (как в нашем случае с соленоидом).

В общей теории показывается, что энергию W можно выра­зить через векторы и в любом случае (но при отсутствии ферромагнетиков) по формуле (3)

Подынтегральное выражение в этом уравнении имеет смысл энергии, заключенной в элементе объемом dV.

Отсюда, как и в случае электрического поля, мы приходим к выводу, что магнитная энергия также локализована в про­странстве, занимаемом магнитным полем.

Из формул (2) и (3) следует, что магнитная энергия распределена в пространстве с объемной плотностью

Отметим, что полученное выражение относится лишь к тем средам, для которых зависимость от линейная, т. е. в со­отношении не зависит от . Другими словами, выра­жения (2) и (3) относятся только к пара- и диамагнетикам. К ферромагнетикам они не применимы.

Отметим также, что магнитная энергия — величина сущест­венно положительная.

38. (1 из 1) Работа перемагничивания ферромагнетика.

39. (1 из 2) Уравнения Максвелла в пустоте.

Изменения тока в цепи сопровождаются совершением против ЭДС самоиндукции работы:

в отсутствии ферромагнетиков вся работа идет на создание энергии магн. поля: и (т.к. ф-ция состояния )

Возьмем бесконечный соленоид: след. где V=lS объем соленоида, заполним соленоид ферромагнетиком.

Связь H и B показана на рисунке. HdB- заштр. участок. Следовательно след. . Следовательно что при наличии ферромагнетиков работа не может быть приравнена к приращению энергии. Работа идет на увеличение внутренней энергии ферромагнетика т.е. на его нагревание. При совершении одного цикла перемагничивания ферромагнетика затрачивается на единицу объема работа

В интегральной форме система уравнений Максвелла име­ет следующий вид:

где — объемная плотность сторонних зарядов, — плотность тока проводимости.

Эти уравнения в сжатой форме выражают всю совокупность наших сведений об электромагнитном поле. Содержание этих уравнений заключается в следующем:

1. Циркуляция вектора по любому замкнутому контуру равна со знаком минус производной по времени от магнитного потока через любую поверхность, ограниченную данным конту­ром. При этом под понимается не только вихревое электриче­ское поле, но и электростатическое (циркуляция последнего, как известно, равна нулю).

2. Поток вектора сквозь произвольную замкнутую поверх­ность всегда равен нулю.

3. Циркуляция вектора по любому замкнутому контуру равна полному току (току проводимости и току смещения) че­рез произвольную поверхность, ограниченную данным конту­ром.

4. Поток вектора сквозь любую замкнутую поверхность равен алгебраической сумме сторонних зарядов, охватываемых этой поверхностью.

Из уравнений Максвелла для циркуляции векторов и следует, что электрическое и магнитное поля нельзя рассмат­ривать как независимые: изменение во времени одного из этих полей приводит к появлению другого. Поэтому имеет смысл лишь совокупность этих полей, описывающая единое электро­магнитное поле.

39. (2 из 2) Уравнения Максвелла в пустоте.

Если же поля стационарны (=const и =const), то уравне­ния Максвелла распадаются на две группы независимых урав­нений:

В этом случае электрическое и магнитное поля независимы друг от друга, что и позволило нам изучить сначала постоянное электрическое поле, а затем независимо от него и постоянное магнитное поле.

Необходимо подчеркнуть, что рассуждения, с помощью ко­торых мы пришли к уравнениям Максвелла, ни в коей мере не могут претендовать на их доказательство. Эти уравнения нельзя «вывести», они являются основными аксиомами, постулата­ми электродинамики, полученными путем обобщения опытных фактов. Эти постулаты играют в электродинамике такую же роль, как законы Ньютона в классической механике или нача­ла термодинамики.

Уравнения Максвелла в дифференциальной форме. Уравне­ния (1) и (2) можно представить в дифференциальной форме, т. е. в виде системы дифференциальных уравнений, а именно: