
Шпоры по Электричеству и магнетизму / Новая папка (3) / Физика / !full
.doc|
1. (1 из 1)Закон Кулона. Принцип суперпозиции полей. |
2. (1 из 2) Потенциальная энергия заряда в поле. Потенциал. |
|
Закон
Кулона. Из
опыта непосредственно следует, что
напряженность поля неподвижного
точечного заряда q
на
расстоянии
где
заряд
q
определяют
в кулонах
(Кл),
напряженность поля
Заметим еще, что в поле, создаваемом неподвижным точечным зарядом, сила, действующая на пробный заряд, не зависит от того, покоится пробный заряд или движется. Это относится и к системе неподвижных зарядов. Принцип суперпозиции. Напряженность поля системы точечных неподвижных зарядов равна векторной сумме напряженностей полей, которые создавали бы каждый из зарядов в отдельности:
где
Это утверждение называют принципом суперпозиции (наложения) электрических полей. Он выражает одно из самых замечательных свойств полей и позволяет вычислять напряженность поля любой системы зарядов, представив ее в виде совокупности точечных зарядов, вклад каждого из которых дается формулой (*). |
Потенциал.
До сих пор мы рассматривали описание
электрического
поля с помощью вектора
Тот
факт, что линейный интеграл
где
Потенциалу
какой-либо произвольной точки О
поля
можно условно
приписать любое значение
Таким
образом, потенциал
Единицей потенциала является вольт (В).
|
|
2. (2 из 2) Потенциальная энергия заряда в поле. Потенциал. |
3. (1 из 2) Связь напряжённости электрического поля и потенциала. Циркуляция вектора напряжённости. |
|
Потенциальная
энергия заряда в поле.
Формула (1) содержит не
только определение потенциала
Другими
словами, если известно поле
Найдем таким способом потенциал поля неподвижного точечного заряда:
где
учтено, что
Отсутствие
в этом выражении аддитивной константы
означает, что мы условно полагаем
потенциал на бесконечности
|
Связь
напряжённости электрического поля и
потенциала.
Электрическое поле полностью описывается
векторной функцией
Связь
между
где
где
символ частной производной подчеркивает,
что функцию
Рассуждая
аналогично, можно получить соответствующие
выражения
для проекций
Величина,
стоящая в скобках, есть не что иное,
как градиент
потенциала
Циркуляция вектора напряжённости. Из механики известно, что любое стационарное поле центральных сил является потенциальным, т.е. работа сил этого поля не зависит от пути, а зависит только от положения начальной и конечной точки. Именно таким свойством обладает |
|
3. (2 из 2) Связь напряжённости электрического поля и потенциала. Циркуляция вектора напряжённости |
4. (1 из 2) Поле электрического диполя. |
|
электростатическое
поле — поле, образованное
системой неподвижных зарядов. Если в
качестве пробного заряда,
переносимого из точки 1
заданного
поля
Как
мы сейчас покажем, из независимости
линейного интеграла
от пути между двумя точками следует,
что по произвольному
замкнутому пути этот интеграл равен
нулю. Интеграл
по замкнутому пути называют циркуляцией
вектора
И
Для
доказательства этой Th
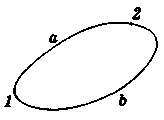
разобьем произвольный замкнутый
путь на две части 1а2
и
2b1
(рисунок).
Так как линейный интеграл
|
Электрический
диполь —
это система из двух одинаковых по
модулю разноименных точечных зарядов
+q
и
-q,
находящихся
на некотором расстоянии
Поле диполя обладает осевой симметрией, поэтому картина поля в любой плоскости, проходящей через ось диполя, одна и та же и вектор Е лежит в этой плоскости.
Найдем
сначала потенциал поля диполя, а затем
его напряженность.
Согласно
Так
как
ный!). С учетом этого
где
|
|
4. (2 из 2) Поле электрического диполя. |
5. (1 из 2) Сила, действующая на диполь в неоднородном поле. |
|
положительному:
где
q
> О
и
Из
формулы (1.34) видно, что поле диполя
зависит от его электрического
момента
Следует
также обратить внимание на то, что
потенциал поля диполя убывает с
расстоянием
Для
нахождения поля диполя воспользуемся
формулой
Отсюда
модуль вектора
В
частности, при
т.
е. при одном и том же
|
П
Разность Е+ - Е_ — это приращение АЕ вектора Е на отрезке, равном длине диполя I, в направлении вектора 1. Вследствие малости этого отрезка можно записать
После подстановки этого выражения в формулу для F получим, что сила, действующая на диполь:
где
р
=
ql
—
электрический момент диполя. Входящую
в это выражение
производную принято называть производной
вектора
по направлению. Знак частной производной
подчеркивает, что эта производная
берется по определенному направлению
— направлению,
совпадающему с вектором
П
|
|
5. (2 из 2) Сила, действующая на диполь в неоднородном поле. |
6. (1 из 1) Дипольный момент системы зарядов. |
|
Н
Если
нас интересует проекция силы
где
П
Если
же вектор
|
Р
плечо
которой равно
где
Полученную формулу можно представить в векторном виде как
Этот
момент сил стремится повернуть диполь
так, чтобы его электрический
момент
В
неоднородном электрическом поле
диполь будет вести себя следующим
образом: под действием момента сил
|


 так,
мы утверждаем, что циркуляция вектора
Е в любом электростатическом
поле
равна нулю, т.е.
так,
мы утверждаем, что циркуляция вектора
Е в любом электростатическом
поле
равна нулю, т.е.
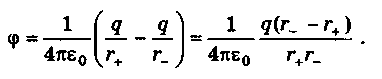
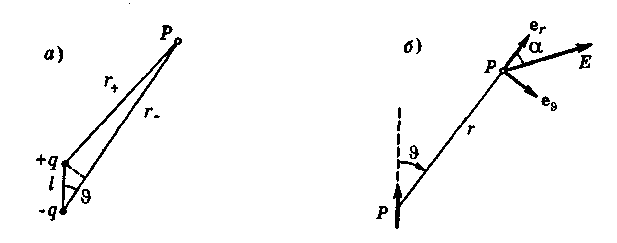
 оместим
диполь во внешнее неоднородное
электрическое поле. Пусть Е+
и Е_ — напряженности
внешнего поля в точках, где расположены
положительный
и отрицательный заряды диполя. Тогда
результирующая сила
F,
действующая на диполь, равна:
оместим
диполь во внешнее неоднородное
электрическое поле. Пусть Е+
и Е_ — напряженности
внешнего поля в точках, где расположены
положительный
и отрицательный заряды диполя. Тогда
результирующая сила
F,
действующая на диполь, равна: ростота
формулы
ростота
формулы
 а
рисунке показаны направления силы
а
рисунке показаны направления силы
 усть
диполь с моментом
усть
диполь с моментом
 ассмотрим,
как ведет себя электрический диполь
ассмотрим,
как ведет себя электрический диполь