Двухмерное смещение

Отметим, что в общей матрице 2*2 ввести константу переноса в общую структуру матрицы не представляется возможным.

Эту трудность можно устранить путем введения третьей компоненты для векторных точек.

→

В результате матрица преобразований превращается в размеры 3*2 и имеет вид:

Такая структура объясняется тем, что число столбцов матрицы, описывающих точку, должны равняться числу строк матрицы, выполняющих преобразование.

Преобразование будет выглядеть следующим образом:

* = =

Отсюда видно, что константы m и n вызывают смещение точки относительно точки с координатами (x; y), поскольку матрица 3*2 не является квадратной, следовательно, нельзя построить обратную матрицу. Эту трудность можно устранить, дополнив матрицу преобразований до квадратной.

Заметим, что третья компонента вектора положения точек не изменяет. Используя эту матрицу преобразований, получим:

Т.о. вектор положений (x; y) около точек m и n может быть выполнен с помощью преобразования:

= *

Трехмерное преобразование и проекции

Введем трехмерные координаты. Точка (X, Y, Z, H) представляется в четырехмерном пространстве (x, y, z, 1).

Преобразование неоднородных координат (X, Y, Z, H) в однородные (x, y, z, 1) производится через матрицу Т.

(X, Y, Z, H) = (x, y, z, 1) * Т

Рассмотрим частные случаи для данного четырехмерного преобразования.

Трехмерное изменение масштаба

Частное изменение масштаба:

Данное преобразование производит частное изменение масштаба.

Общее изменение масштаба получается засчет использования четвертого диагонального элемента.

, , .

Сдвиг

Недиагональные элементы левой верхней подматрицы 3*3 в общем матричном преобразовании 4*4 осуществляют сдвиг в трех измерениях и имеют вид:

Трехмерное вращение

Рассмотрим несколько частных случаев вращения.

При вращении вдоль оси X, размеры вдоль оси X не изменяются.

Т.о. матрица преобразований будет иметь нули в первой строке и столбце за исключением единицы на главной диагонали.

θ - угол вращения вокруг оси X

Вращение положительно по часовой стрелке, если смотреть вдоль оси вращения с начала координат.

Для выражения на угол около оси Y нули ставятся во второй строке и столбце матрицы преобразования, за исключением единицы на главной диагонали.

Матрица примет вид:

Аналогична матрица преобразований на угол ψ около оси Z:

Т.к. вращение описывается умножением матриц, то трехмерное вращение не коммутативно, т.е. порядок умножения будет влиять на конечный результат.

Отображение в пространстве

Иногда требуется выполнить зеркальное отображение трехмерного объекта.

Рассмотрим частные случаи этого отображения.

Матрица преобразований плоскости XY будет иметь вид:

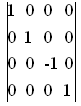
Дальнейшее преобразование (XZ и YZ) можно получить разными способами: путем вращения и отображения или просто отображением.

Для отображения YZ:

Для отображения XZ: