1. Пространство элементарных исходов

Пространством элементарных исходов (событий) Ω наз. мн-во содержащая все возможные исходы данного случайного эксперимента, из которых в эксперименте происходит ровно один.

2. Элементарный исход (событие)

Элементы мн-ва Ω наз. элементарными событиями (исходами) и обозначается w. Ω={w₁,w₂,…,w_n,…}.

3. Событие

События наз. произвольное подмножество ПЭИ Ω, т.е любой набор элементарных исходов.

4. Достоверное событие

Событие состоящее из всех элементарных исходов, т.е. событие которое обязательно произойдет наз. достоверным и совпадает с Ω.

5. Невозможное событие

Событие не содержащее ни одного элементарного исхода, т.е. которая никогда не происходит в данном опыте наз. невозможным и обозначается «∅».

6. Пересечение (произведение) 2 событий

Пересечение (произведение) 2 событий А и В наз. события С происходящее тогда и только тогда когда одновременно происходят оба события А и В, т.е. события состоящие из тех и только тех элементарных исходов которое принадлежит и А и В, и обозначаются C=A∩B или C=AB.

7. Несовместные события

События А и В наз. несовместными, если их пересечения яв-ся невозможным событием А∩В=∅, в противном случае событие наз. совместным.

8. Объединение (сумма) 2 событий

Объединением (суммой) 2 событий А и В наз. событие С происходящее тогда и только тогда, когда происходит хотя бы одно из событий А или В, обозначается С=АUВ или С=А+В («+» - если известно, что А и В - несовместны).

9. Попарно несовместные события

События А₁,А₂,...,А_n наз. попарно несовместными, если А_i A_j=∅ , i≠j.

10. Противоположное событие

Противоположное к событию А наз. событие Ā которые происходят тогда и только тогда, когда А не происходит.

11. Равносильные события

Если А и В⊂А, то событие А и В наз. равносильными или равными (В=А).

12. Полная группа событий

События А₁,А₂,...,А_n образуют полную группу событий если:

а) События попарно не совместны,

б) Сумма этих событий есть достоверное событие (А₁+А₂+…+А_n= Ω).

13. Законы Моргана на примере 2 событий

14. Правило суммы.

Если объект А может быть выбран m способами, а объект В может быть выбран другими n способами, то выбор одного элемента A или B из объединённой совокупности может быть осуществлен из m+n способами.

15. Правило произведения.

Если объект А может быть выбран m способами и после каждого такого выбора объект В может быть извлечён n способами, то выбор пары объекта А и В, в указанном порядке может быть осуществлен m*n способами.

16. Выборка

Результат выбора m элементов из группы содержащей n элементов будем наз. выборкой из m по n элементов.

17. Выборка с возвращением

Если при выборке элемент после выбора снова возвращается в группу, то выборку наз. выборкой с возвращением.

18. Сочетание

Выборку в которой не учитывают порядок выбора элементов наз. сочетанием.

19. Размещение Выборку в которой учитывают порядок выбора элементов наз. размещением.

20. Сочетание и размещения с повторением

Если рассматривать выборку с возвращением, то сочетание (размещения) наз. сочетанием (размещением) с повторением.

21. Перестановка

Размещение без повторений из n элементов по n элементов наз. перестановкой из n элементов.

22. Число размещения без повторения

А_n^m= .

23. Число сочетание без повторений

С_n^m= .

24. Число перестановок

P_n=n!

25. Число размещений с повторениями

Ã_n^m=n^m.

26. Число сочетаний с повторениями

Ĉ_n^m=С_n+m-1^m.

27. Вероятность элементарного исхода

Число p(w_i) наз. вероятностью элементарного исхода w_i.

28. Вероятность события на дискретном пространстве ЭИ

Вероятность любого события А Ω, будем определять по формуле , т.е. вероятность события А ровна сумме вероятностей ЭИ входящих в мн-во А.

29. Свойства вероятности

1) Р( )=0 2) Р(Ω)=1

3) 0 Р(А)≤1

4) Р(А В)=Р(А)+Р(В)-Р(АВ)

5) Р(А+В)=Р(А)+Р(В), А,В-несовместны

6) Р(А)=1-Р(А)

30. Предположения классической вероятностной модели

1) ПЭИ состоит из конечного числа n элементов исходов Ω={w₁,w₂,...,w_n}

2) все ЭИ равновозможны, поэтому вероятность любого из них равна p(w_i)=1/n, i=1,n.

31. Классическое определение вероятности

Если экспериментально удовлетворяет условием классической вероятностной модели, то вероятность событие А вычисляется по формуле: Р(А)=к/n.

32. Предложения геометрическое вероятностной модели

1) ПЭИ Ω имеют конечную меру

2) вероятность попадание случайной брошенной точки любого подмножества Ω пропорционально мере этого подмножества и не зависит от его расположение и формы.

33. Геометрическое определение вероятности

Вероятность попадания в область А⊆Ω, при бросании на удачу точки в области Ω равна: Р(А)=µ(А)/µ(Ω), где µ-это мера множества.

34. Аксиоматическое определение вероятности

Вероятность (Ω,F)- это числовая функция определенная на множествах из σ -алгебра F и обладающая следующими свойствами:

Аксиома 1: Р(А)>=0 А F

Аксиома 2: Р(Ω)=1

Аксиома 3: если послед событий {А_n} такова, что событие попарно несовместны, т.е. A_iA_j=∅ i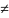 j, то вероятность объединения Р(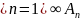 )= A_n).

35) Вероятностное пространство  Совокупность ( )  будем называть вероятностным пространством с вероятностной мерой Р

36 Событие на вероятностном пространстве

Элементы сигмы –алгебры т.е А будем наз событиями.

37. Условная вероятность

Условной вероятностью события А при условии событие В с Р(В)>0 наз. величина P(A/B)=P(AB)/P(B), P(B/A)=P(AB)/P(A).

38. Независимость 2 событий А и В

Событие А и В наз. независимыми, если Р(АВ)=Р(А)Р(В).

39. Независимость событий в совокупности

Случайные событие А₁,...,А_n наз. независимыми в совокупности, если вероятность: Р(А₁,..,А_n)=Р(А₁)...Р(А_n).

40. Попарная независимость

События А₁,..,А_n наз. попарно независимы, если для i,j=1,n, i j P(A_iA_j)=P(A_i)P(A_j)

41. Формула умножения вероятностей для двух событий

P(AB)=P(A)P(B/A) или P(AB)=P(В)P(А/В).

42. Теорема умножения вероятностей

Если события А₁,..,А_n таковы, что Р(А₁,..,А_n-1)>0,то Р(А₁,..,А_n)=Р(А₁)Р(А₂/А₁)Р(А₃/А₁А₂)…Р(А_n-1/А_1…А_n-2)Р(А_n/А_1…А_n-1).

43.Упрощенная формула для расчёта вероятности наступления хотя бы одного из независимых событий.

Р(Ã)=1-(1-Р(А₁))(1-Р(А₂))..(1-Р(А_n))

44.Теорема. Формула полной вероятности

Пусть Н₁,...,Н_n полная группа событий и событие А содержится в их сумме А⊂ _I , тогда имеет место формула полной вероятности. P(A)= H_i)P(A/H_i)

45. Теорема формула Байесса.

Пусть Н₁,..,Н_n полная группа событий и А⊂ _I причём

Р(А)>0

Р(H_i/A)=(P(H_i)P(A/H_i))/P(A)= (P(H_i)P(A/H_i))/ _i)P(A/H_i))

46.Какие события наз. гипотезами при рассмотрении ф-лы полной вероятости

Попарно несовместные события H₁,H₂,H₃…H_n, образующие полную группу, называют гипотезами.

47.Сумма вероятностей гипотез

Р(H_i/A)=(P(H_i)P(A/H_i))/ _i)P(A/H_i))

48.Схемой независимых испытаний Бернули называется последовательность испытаний удовлетворяющих следующим условием

1)при каждом испытании различают лишь 2 исхода: появление некоторого событие А, что называеться «успехом» либо появление его дополнения А называеться «неудачником»

2)испытание являються независимы

3)вероятность успеха во всех испытаний постоянна и равна Р(А)=р, тогда неудачи Р( )=1-p=q

49 Формула Бернулли

Вероятность P_n(m) того, что в n испытаниях по схеме Бернули P_k,n постоянна, то вероятность того, что событие A наступит k раз в n независимых испытаниях, равна: P_n(m)=C_n^mp^mq^n-m, m=0,n

50. Определение наиболее вероятного числа успехов с схеме Бернули

Число m₀ при котором вероятность. P_n(m) достигает max значения называется найвероятностным числовым успехом.

51.Неравенство для определения наиболее вероятного числа успехов в схеме Бернулли

np-q≤ m₀≤np+p

52. Общая теорема о повторении опытов.

Вероятность того, что событие A в n независимых опытах появится ровно m раз, равна коэффициенту при в выражении производящей функции: , где – вероятность появления события A в i-м опыте, .

53Локальна предельная теорема Муавра-Лапласа:

При большом числе испытаний справедлива формула:

P_n(m)≈1/(npq)^1/2*ψ(x), где ψ(x)=1/(2*Pi)^1/2*е^—x*x/2,

x=(m-np)/(npq)^1/2

54. Функция ψ(x) и ее свойства

1)значение можно найти по таблицам приложения

2)четная т.е ψ(-x)=ψ(x)

3)при х →∞ , ψ(x) →0

55. Интегральная предельная теорема Муавра-Лапласа

При большом числе испытаний n вероятность того,что успешных будет заключено от а до в:

P_n(a≤m≤b)=P_n(a,b)≈Ф(х₂)-Ф(х₁), где

Ф(х)=1/(2*Рі)^{1/2 --t*t/2}dt, формула Лапласа

Х₁=a-np/(npq)^1/2 Х₂=b-np/(npq)^1/2

56. Функция Ф(х) и ее свойства

1)значение можно определить по таблицам приложения

2)нечетная Ф(-х)=-Ф(х)

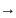3)монотонно возрастает при х _, Ф(х) 0,5

57.Предельная теорема Пуассона или следствие.

При большом числе испытаний n справедливо формула

P_n(m)≈λ^m/m!e^-λ, где λ=np

58.При каких условие каждая из предельных теорем дает хорошее приближение. при λ≤10

59.Значение больших чисел в форме бернулли,

какова бы ни было постоянная ε>0

Р(|m/n-p|<ε) _{n -беск} 1

60. Следствие из теоремы о ЗБЧ Бернулли

Теорема Я. Бернулли утверждает, что при неограниченном увеличении числа опытов n частота события A сходится по вероятности к его вероятности  . Обозначим частоту события A в n опытах через   и запишем теорему Я. Бернулли в виде формулы где,   - сколь угодно малые положительные числа.

56. Как вы понимаете, что такое случайная величина (СВ), привести пример

СВ будем понимать такую величину, которая в результате опыта принимает неизвестные заранее значения, причем это значение от опыта к опыту меняется. Например: Время безотказной работы выбранного электроприбора.

57. Определение СВ

действительная функция 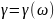определенная на ( наз F – измеримой или СВ, если {w: (w)

58. Определение функции распределения вероятностей СВ

Def функция распределения . Функцией распределения F_ζ(x) СВ ζ наз функция F_ζ(x)=р(w: ζ(w)<x)=P(ζ<x), т.е F_ζ(x) есть вероятность того, что СВ примет значение меньше некоторого х.

59. Свойства функции распределения вероятностей СВ

1⁰.0 F_ζ(x) 1 ,

2⁰. F_ζ(x) не убывающая функция , т.е если х₁ х₂, то F_ζ(x₁) F_ζ(x₂)

3⁰. F_ζ(x) удовл следующим соотношенем F_ζ(x)=0 , 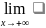F_ζ(x)=1

4⁰.ФР непрерывна слева , т.е F_ζ(x)= F_ζ(x₀)

5⁰.P(x₁ ζ < x₂)= F_ζ(x₂)- F_ζ(x₁)

60. Понятие закона распределения СВ

Понимают всякую характеристику из которой по определенным правилом можно получить функцию распределение СВ.

61. Класификация СВ. Перечислить типы распределений

1)дискретная

2)абсолютно непрерывные

3)сингулярные

62. Определение дискретной СВ (ДСВ) или СВ, имеющей дискретное распределение

СВ ζ имеет дискретные распределения и наз. дискретной, если она принимает конечное или счетное множество значении с определенными вероятностями, т.е существует конечный или счетный набор чисел {x₁,…} такой , что 1)p_i=p(ζ=x_i)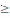 0 2) _i=1

63.Свойство нормировки для ДСВ

_i=1

64.Таблица распределения ДСВ

Таблицей распределения ДСВ ζ называется таблицу вида

ζ	Х1	Х2	……
р	Р1	Р2	……

Где х_{1 <} x₂<….<x_n<….

65. Функция распределения ДСВ

F_ζ(x)=Р(ζ<x)= _i

66. Распределения Бернулли с параметром р

ζ	0	1
р	1-р	р

67. Биномиальное распределение С параметрами n и p, 0 1 имеет СВ ζ

ζ {0,1,2,..N} c вероятностями р_i=p(ζ=i)=C_nⁱ pⁱ q^n-i

68. Геометрическое распределение с парам-ом р, ζ {0,1,2,..} р_i=p(ζ=i)=pⁱq^i-1

69. Распределение Пуассонас параметром λ,λ>0 ,ζ={0,1,.}, p_i=p(ζ=i)=λⁱ/i! *e^-λ

70. Def НСВ, имеющей абсолютно непрерывное распределение СВ ζ имеет абсолютно непрерывные распределения или наз непрерывной , если p_ζ(x) неотрицательная функция, такая что x R функция распределения представима в виде F_ζ(x)= _ζ(t)dt

71. Плотность распределения. Если p_ζ(x) неотрицательная функция, такая что x R функция распределения представима в виде F_ζ(x)= _ζ(t)dt функцию p_ζ(x) наз плотностью распределения вероятностью СВ ζ

72. Свойство нормировки для НСВ _ζ(х)dх=1

73. Свойство плотности распределения вероятностей св

1⁰.р_ζ(х) 0 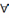x R 2⁰. _ζ(х)dх=1

74. p(a ζ < b)= _ζ(х)dх (с помощью плотности распределения НСВ)

75. Как определить p_ζ(x) через F_ζ(x) p_ζ(x) = F_ζ ^,(x)

76. Как определить F_ζ(x) через p_ζ(x) F_ζ(x)= _ζ(t)dt

77. Плотность распределения равномерного распеределения на отрезке

p_ζ(x) = функция распределения имеет вид

F_ζ(x) =

78. Плотность распределения показательного распределения

p_ζ(x) = функция распределения имеет вид

F_ζ(x) =

79. Плотность распределения вероятностей нормального распределения СВ ζ наз нормальной если её плотность вероятности имеет вид

p_ζ(x) =1/( * )*е^{(-(x-a)*(x-a))/20*0)} значит ζ N(a, ²)

81. Плотность стандартного нормального распределения СВ ζ имеет стандартное нормальное распределения, если а=0, =1 и плотность вероятности имеет вид p_ζ(x) =1/( )*е^(-х*х)/2

83. Хи-квадрат распределения с к степенями свободы имеет сумму квадратов к независимых случайных величин распределенных по стандартным нормальному закону Х²(к)= _i² , где ζ_i N(0,1) ζ_i, i=1,k – независимы

84. Распределение Стьюдента с к-степенями свободы имеет СВ t , t= / , где ζ N(0,1) , 0. Х²(к)- это независимая от ζ СВ имеющее распределение Х² к-степенями свободы

85. Распределения Фишера. С к₁ и к₂ степенями свободы имеет следующие СВ F=(1/k₁* Х²(к₁))/( 1/k₂* Х²(к₂)), где Х²(к₁) и Х²(к₂)- независимые СВ имеющее Х² распределения с к₁ и к₂ степенями свободы.

86. Свойства двумерной функций распределения вероятностей

1⁰.0 F_ζ1ζ2(x₁,x₂) 1 2⁰. F_ζ1ζ2(x₁,x₂) F_ζ1ζ2(y₁,y₂) , x_i y_i , i=1,2

3⁰.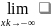 F_ζ1ζ2(x₁,x₂)=0 , F_ζ1ζ2(x₁,x₂)=1

4⁰. F_ζ1ζ2(x₁,x₂)= F_ζ1ζ2(x₁,x₂)

5⁰.ФР двумерной СВ непрерывна слева по каждому из всех аргументов

6⁰. F_ζ1ζ2(x₁,x₂) 0

87. Свойство нормировки для двумерной ДСВ _ij=1

88. Маргинальные распределения P_i=p(ζ₁=x_i)= _{ij ,} P_j=p(ζ₂=x_j)= _ij

89. Свойства двумерной плотности распределения вероятности нсв

1⁰.P _ζ1ζ2(x₁,x₂) 0

2⁰. _ζ1ζ2(x₁,x₂)dx₁dx₂=1

3⁰. p_ζ1ζ2(x₁,x₂)=d²F_ζ1ζ2(x₁,x₂)/( dx₁dx₂)

F_ζ1ζ2(x₁,x₂)= _ζ1ζ2(t₁,t₂)dt₁dt₂

4⁰.p_ζ1(x₁)= _ζ1ζ2(x₁,x₂)dx₂

p_ζ2(x₂)= _ζ1ζ2(x₁,x₂)dx₁

5⁰. P((ζ₁, ζ₂) D)= _ζ1ζ2(x₁,x₂) dx₁dx₂

90. Как в двумерном случае определить плотность распределения вероятности через ФР p_ζ1ζ2(x₁,x₂)=d²F_ζ1ζ2(x₁,x₂)/( dx₁dx₂)

91. Как в двумерном случае определить ФР через плотность распределения вероятностей F_ζ1ζ2(x₁,x₂)= _ζ1ζ2(t₁,t₂)dt₁dt₂

92. Как найти маргиональные плотности по двумернй плотности распред св

p_ζ1(x₁)= _ζ1ζ2(x₁,x₂)dx₂ p_ζ2(x₂)= _ζ1ζ2(x₁,x₂)dx₁

93. Как найти вероятность попадания двумерной св в область d

P((ζ₁, ζ₂) D)= _ζ1ζ2(x₁,x₂) dx₁dx₂

94. Аналогично теоремы умножения

p_ζ(x/y)=(p_ζη(x,y))/p_η(y) p_η(y/x)=(p_ζη(x,y))/p_ζ(x)

95. Критерий независимости НСВ. Случайные величины ζ_1,… ,ζ₂ независимы т.и.т.т,к во всех точках непрерывности функций Р_{ζ1,… ,ζ2}(х₁,…,х_n) P_ζ1(x₁), P_ζ2(x₂),.., P_ζn(x_n), имеет право равенство Р_{ζ1,… ,ζ2}(х₁,…,х_n) = P_ζ1(x₁) …. P_ζn(x_n)

96. Критерий независимости ДСВ. Пусть СВ ζ_i i=1,n –ДСВ, тогда для независимости ζ_i необх и достаточно,чтобы P(ζ₁=k₁,..,ζ_n=k_n)=P(ζ₁=k₁)..p(ζ_n=k_n)

97. n=m=1, f-монотонная функция. Необходимо найти плотность распределения вероятности m-мерной СВ η= (η₁,..,η_n) p_η(y)=p_ζ(g(y))*|g^,(y))|