2.3. Выбор расчетной схемы панели и расчет внутренних усилий в панели.

Панель рассчитывается как изгибаемый элемент в виде стержня. Стержень нагружен в поперечном направлении равномерно распределенной нагрузкой, которая вызывает поперечный изгиб. Стержень свободно (шарнирно) опирается на опоры (сборные ригели). В расчетной схеме панели (рис. 6) условия опирания стержня принимаем с подвижным и неподвижным шарнирами на опорах.

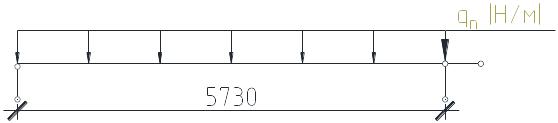
Рис. 6. Расчетная схема сборной панели.

Произведем расчет внутренних усилий (силовых факторов) в панели.

1. Изгибающий момент от полной расчетной нагрузки:

2. Поперечная сила от полной расчетной нагрузки:

3. Изгибающий момент от полной нормативной нагрузки:

3. Изгибающий момент от продолжительно (длительно) действующей нормативной нагрузки:

_{Рис. 7. Эпюры внутренних силовых факторов.}

На рис. 7 показано деление плиты на три расчетных участка: два приопорных участка по четверти пролета и один средний участок равный половине пролета.

2.4. Характеристики арматуры и бетона.

Напрягаемая арматура А800 (A-V). Для А800 находим:

В качестве ненапрягаемой арматуры предусматриваем арматуру класса B500:

Класса бетона – B30:

2.5. Выбор величины исходного предварительного напряжения в напрягаемой арматуре.

Согласно п. 2.2.3.1 [8] предварительные напряжения арматуры принимают для горячекатаной и термомеханически упрочненной арматуры (класс арматуры по прочности на растяжение – А) не более .

исходная (начальная) величина предварительного напряжения.

_{С увеличением величины} увеличивается значение потерь предварительного напряжения. Поэтому, а также с целью повышения безопасности при производстве работ по натяжению арматуры, принимаем

Согласно п.3.1.1.6 [8] при расчете предварительно напряженных элементов по прочности следует учитывать возможные отклонения предварительного напряжения (или усилия обжатия P) путем умножения на коэффициент

коэффициент точности натяжения арматур.

Значения коэффициента принимают равным:

1) - при благоприятном влиянии предварительного напряжения;

_{Например: расчет на ширину раскрытия трещин – чем больше P, тем меньше ширина раскрытия трещин при эксплуатации конструкции;}

_{P = 100 кН – мастер при натяжение ставит 100 кН, а в расчете стоит 90 кН;}

₂₎ - при неблагоприятном влиянии предварительного напряжения;

Например: расчет на прочность в стадии транспортирования – чем больше P, тем больше растягивающие напряжения в верхней части сечения, в которой при эксплуатации возникают только сжимающие напряжения;

P=100 кН – мастер при натяжении ставит 100 кН, а в расчете стоит 110 кН.

2.6. Подбор продольной напрягаемой рабочей арматуры из условия прочности сечения, нормального к продольной оси панели.

_{Расчет реального сечения многопустотной панели является очень трудоемким процессом, поэтому для упрощения математических вычислений преобразуем реальное сечение к приведенному сечению, которое будет равнозначно реальному.}

_{Приводим окружности к равнозначным прямоугольникам (рис.8). Какие-либо геометрические фигуры являются равнозначными, если у них одинаковы площади и моменты инерции. На рис.9 представлено полученное приведенное сечение многопустотной панели в виде двутавра.}

_{Рис.8. Преобразование к приведенному сечению.}

1-е условие равнозначности: то есть

2-е условие равнозначности: то есть

Зная диаметр круга (d=160 мм), мы получаем два уравнения с двумя неизвестными b и h. После несложных алгебраических преобразований получаем:

b=145,1 мм и h=138,6 мм.

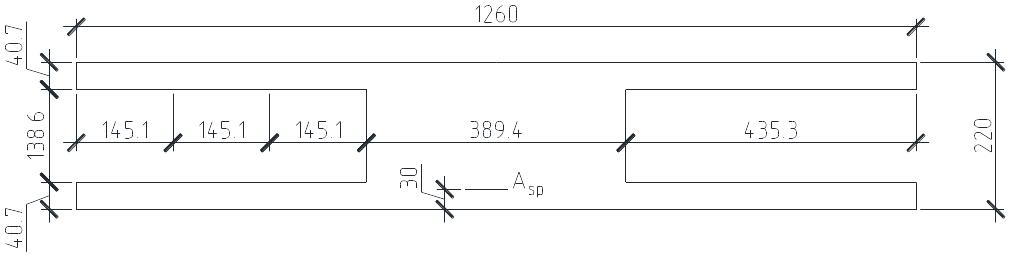
Рис.9. Приведенное сечение многопустотной панели (двутавр).

На рис. 9 показаны геометрические параметры приведенного сечения:

ширина полки двутаврового сечения,

ширина ребра двутаврового сечения,

_{высота полки двутаврого сечения,}

высота двутаврового сечения (поперечного сечения панели),

расстояние от центра тяжести площади поперечного сечения (рис.10);

площадь поперечного сечения предварительно напряженной арматуры.

Первоначально величина принимается приблизительно, исходя из опыта проектирования, а впоследствии, после подбора 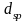, проверяется снова, с учетом величины . Величина должна удовлетворять следующему условию:

где: - диаметр предварительно напряженной арматуры;

- толщина защитного слоя бетона (расстояние от поверхности арматуры до грани конструкции).

Согласно п. 5.2.1 СП [8] толщину защитного слоя бетона арматуры предварительно напряженных элементов принимают не менее указанной в табл. 8.1 СП [7]. Согласно табл. 8.1 СП [7] минимальное значение толщины защитного слоя бетона рабочей арматуры равно 25 мм (в закрытых помещениях при повышенной влажности).

Согласно 8.3.2 [7] для сборных элементов минимальные значения толщины защитного слоя бетона рабочей арматуры уменьшают на 5мм. Во всех случаях толщину защитного слоя бетона принимают не менее диаметра стержня арматуры, то есть d_sp.

В задании на курсовой проект дана относительная влажность воздуха в помещении φ_int = 75%, то есть нормальная влажность (φ_int ≥ 75%). Рассчитываемая панель является сборным элементов. Таким образом, в данном случае минимальное значение а_зс равно 20 мм (при диаметре арматуры d_sp менее 20 мм).

а_зс ≥ 20 мм и а_зс ≥ d_sp.

Рис.10. Определение в сечении.

Определим рабочую высоту сечения:

Согласно п. 2.1.2.3 [8] влияние длительности действия статической нагрузки учитывается коэффициентом условий работы бетона γ_bl, вводимым к расчетным значениям сопротивлений R_b и R_bt и принимаемым равным:

γ_bl = 1,0 – при непродолжительном (кратковременном) действии нагрузки;

γ_bl = 0,9 – при продолжительном (длительном) действии нагрузки.

Определяем х – высоту сжатой зоны бетона:

х = 19 мм < h_f = 40,7 мм, следовательно, граница сжатой зоны бетона проходит в полке.

Предполагаем, что выполняется условие ξ ≤ ξ_R, то есть рассчитываемся сборная панель разрушается по 1-му случаю разрушения железобетонной конструкции (разрыв растянутой арматуры).

Определяем требуемую площадь поперечного сечения предварительно напряженной арматуры А_sp,т. Отметим, что А_sp,т находится без учета наличия в арматуре преднапряжений σ_sp. Подбор А_sp,т производится, как и подбор А_s,т для железобетонных конструкций без предварительного напряжения арматуры, из условия равенства усилий, воспринимаемых растянутой арматурой и сжатым бетоном, то есть из условия N_s = N_b (A_sp*R_s = A_b*R_b).

Для предварительно напряженных элементов применяется стержневая арматура периодического профиля диаметром 10…18 мм (включительно).

Принимаем 5Ø12 А800 с площадью A_sp = 5,65 см².

Проверяем величину a_sp с учетом принятой величины d_sp = 12 мм:

а_sp = 30 мм ≥ а_зс + 0,5 d_sp = 20 + 0,5·12 = 26 мм – условие выполняется.