3.14. Расчет длин запуска обрываемых в пролете стержней продольной арматуры за точки их теоретического обрыва

Для обеспечения прочности наклонных сечений главной балки по изгибающим моментам обрываемые в пролете стержни продольной арматуры необходимо завести за точку теоретического обрыва на расстояние:

W ,

где: Q-поперечная сила в точке теоретического обрыва стержня;

q -несущая способность поперечного армирования балки в точке теоретического обрыва;

d-диаметр обрываемого стержня.

Кроме того, общая длина запуска стержня за точку теоретического обрыва должна быть не менее 20*d и не менее 250 мм.

На участке 1 главной балки (см. рис. 57) имеем:

Q = Q = 2976 МПа*см², q = 17,79 МПа*см.

d = 22 мм W = = 94,6 см = 946 мм;

d = 32 мм W = = 99,6 см = 996 мм.

На участке 2 главной балки имеем:

Q = Q = 795 МПа*см², q = = 6,51 МПа*см

d = 22 мм W = =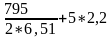 72,0 см = 720 мм.

На участке 3 главной балки имеем:

Q = Q = 4534,3 МПа*см², q = 19,05 + 25,61 = 44,66 МПа*см

d = 22 мм W = = 61,8 см = 618 мм;

d = 25 мм W = = 63,3 см = 633 мм;

d = 32 мм W = =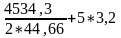 66,8 см = 668 мм;

d = 36 мм W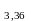 = =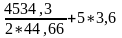 68,8 см = 688 мм.

На участке 4 главной балки имеем:

Q = Q = 3755 МПа*см², q = 19,05 + 25,61 = 44,66 МПа*см

d = 20 мм W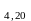 = = 52 см = 520 мм;

d = 25 мм W = = 54,5 см = 545 мм;

d = 36 мм W = = 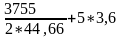60 см = 600 мм;

На участке 5 главной балки обрывов продольной арматуры нет.

На рис. 57 указаны найденные длины запуска стержней продольной арматуры за точки теоретического обрыва, а на рис. 58 показаны схема расположения и рабочие чертежи арматурных каркасов главной балки. В табл. 5 приведена спецификация материалов на главную балку.

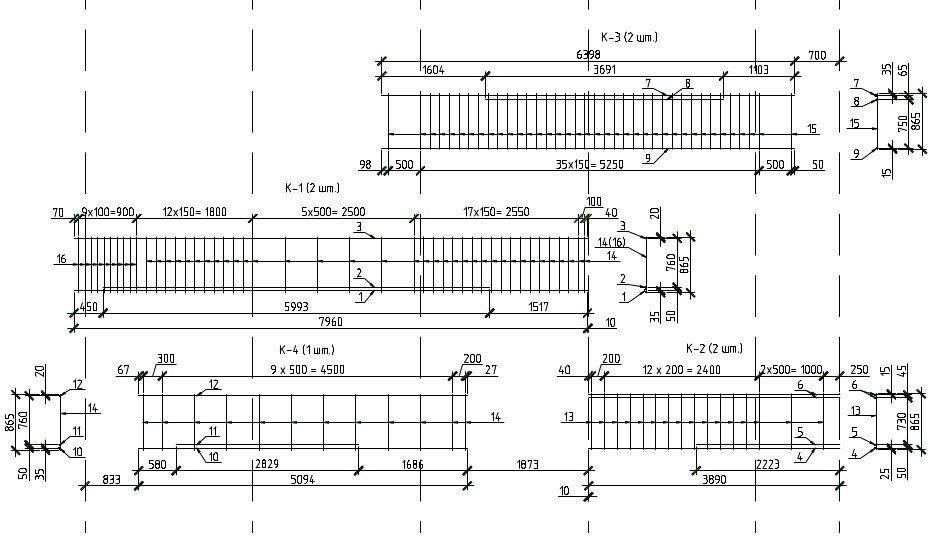Рис 58 Арматурные каркасы главной балки и их размещение

Таблица 5

Спецификация материалов главной балки

Формат	Зона	Поз.	Обозначение	Наименование	Кол-во	Примечание (вес, кг)
				Каркасы плоские

3.3.7. Проверка прочности наклонного сечения по грани свободной опоры на действие изгибающего момента

Расчетная схема наклонного сечения главной балки на свободной опоре показана на рис. 59. Изгибающий момент в наклонном сечении воспринимается продольной арматурой, доведенной до опоры, и поперечной арматурой балки в пределах наклонной трещины.

До опоры доведена арматура из двух стержней Ø32 мм и двух стержней Ø22 мм (см. рис 57). Расчетное усилие в этих арматурах определяется с учетом коэффициента условия работы, равного 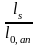, вводимого в расчет при недостаточной анкеровке арматуры. Длина запуска указанных стержней за грань опоры составляет 37 см.

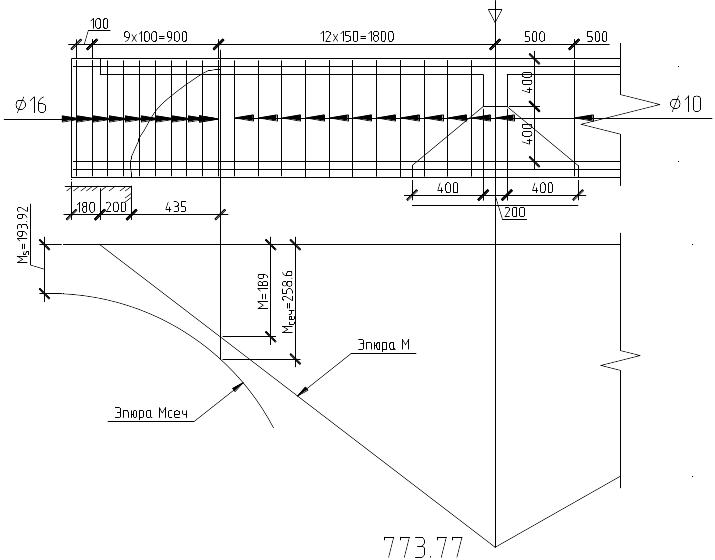
Рис. 59. Расчетная схема наклонного сечения по изгибающему моменту у свободной опоры главной балки

По формуле (8.1) [1] рассчитываем базовую длину анкеровки продольной арматуры:

-для стержней Ø32:

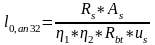= = 115,25 см;

-для стержней Ø22:

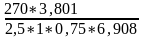= = 79,23 см;

Соответствующие коэффициенты условий работы:

-для стержней Ø32 мм = 37/115,25 = 0,321;

-для стержней Ø22 мм = 37/79,23 = 0,467.

Вычисляем долю изгибающего момента, воспринимаемую доведенной до опоры арматурой:

A = 16,08 см² (2Ø32 A300), а = 5 см;

A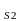 = 7,6 см² (2Ø22 A400), а = 10 см.

N = 0,321*R * A = 1393,6 МПа*см²;

N = 0,467*R * A = 958,3 МПа*см²;

а = = = 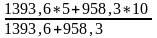7,037 см;

х = = = 1,025 см;

Z = h – a – 0,5*x = 90 – 7,037 – 0,5*1,025 = 82,45 см;

М = (N + N )*z = 193915 Н*м.

Так как эпюра моментов главной балки на приопорном участке линейна, то длину проекции наиболее опасного наклонного сечения определяем по формуле:

с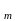 = = 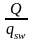= 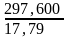16,73 кН/МПа*см = 1,673 м > 2* h =2*85 = 170 см.

Принимаем с =170 см.

Тогда величина действующего в опасном наклонном сечении изгибающего момента:

М = Q*( с +с ) = 297,6*(1,7+0,2) = 565,44 кН*м.

Несущая способность заданного наклонного сечения по изгибающему моменту:

М = М +q *0,5* = 193,92 + 177,9*1,7²*0,5 = 451 кН*м < 565,44 кН*м

Следовательно, прочность наклонного сечения главной балки на свободной опоре не обеспечена.

Для обеспечения прочности данного сечения усиливаем поперечное армирование на приопорном участке главной балки, для этого в каркасах К-1 на длине 800 мм от оси опоры устанавливаем поперечные стержни Ø16 мм из стали А240 с шагом 100 мм.

Тогда интенсивность поперечного армирования на этом участке:

q = = 68,34 МПа*см.

Проекция наиболее опасного наклонного сечения:

с = = 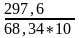= 0,435 м < 0,8м (зона усиления поперечной арматуры, см рис. 59).

Внешний момент в наклонном сечении:

М = 297,6*(0,435 + 0,2) = 189 кН*м.

Несущая способность наклонного сечения по изгибающему моменту:

М = М +q * /2 = 193,92 + 68,34*0,435²*10/2 = 258,6 кН*м > 189 кН*м.

Следовательно, прочность наклонного сечения главной балки по изгибающему моменту на свободной опоре обеспечена.

На рис. 58 конструкция каркасов К-1 принята с учетом выполненных изменений.