2. Способы задания функции.

Существует несколько способов задания функции.

Табличный. Используется тогда, когда область определения состоит из

конечного множества чисел. Тогда для задания функции проще всего указать

таблицу, содержащую значения аргумента и соответствующие значения

функции. Например, таблица логарифмов. Другим примером могут быть

таблицы, содержащие данные о числе жителей, населяющих земной шар в

отдельные годы, расписания движения поездов и т.п.

Аналитический. При аналитическом способе задания функция может

быть задана явно, когда дано выражение у через x, т.е. формула имеет вид

y  f (x) ; неявно, когда х и у связаны между собой уравнением вида F(x, y)  0 ;

параметрически, когда соответствующие друг другу значения х и у выражены

через третью переменную величину t, называемую параметром.

Логический. Если функция описывается правилом ее составления,

например, функция Дирихле: f(x)= 1, если x – рациональное; f(x)= 0, если x –

иррациональное.

Графический. Состоит в изображении графика функции – множества

точек (x, y) плоскости, абсциссы которых есть значения аргумента x, а

ординаты – соответствующие им значения функции y  f (x) . Преимуществом

графического задания является его наглядность, недостатком – его

неточность.

32.

Определение элементарной функции. Функции, которые могут быть получены из основных элементарных функций посредством арифметических действий (сложение, вычитание, умножение, деление) и образования сложных функций, называютсяэлементарными функциями . Примером может являться функция 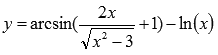 Очень удобно классификацию элементарных функций представить в виде таблицы.

• Элементарные функции

• Трансцендентные

• Алгебраические

• Иррациональные

• Рациональные

• Целые рациональные

• Дробные рациональные

Элементарные функции подразделяются на алгебраические и трансцендентные. Определение алгебраических функций. Алгебраическими называют функции, составленные из букв и цифр, соединенных знаками действий сложение, умножение, вычитание, деление, возведение в целую степень и извлечение корня. Другими словами: алгебраическими называют элементарные функции, которые могут быть получены из двух основных функций f(x)=x и f(x)=1 при помощи любого числа последовательно выполненных алгебраических действий (сложение, умножение, вычитание, деление, возведение в целую степень, извлечение корня) и умножения на числовые коэффициенты. Например, функция 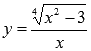  является алгебраической. Определение трансцендентной функции. Трансцендентными называют элементарные функции, которые не являются алгебраическими. (То есть, они образованы при помощи возведения в иррациональную степень, логарифмирования, с использованием тригонометрических и обратных тригонометрических операций). К примеру, 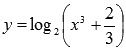  - трансцендентная функция. Алгебраические функции подразделяются на рациональные и иррациональные . Рациональные функции разделяются на целые рациональные функции (многочлены) и дробные рациональные (отношение многочленов). Пример целой рациональной функции:  . Пример дробно-рациональной функции:  . ПРИМЕЧАНИЕ: Рациональные функции могут содержать и иррациональные коэффициенты (главное, чтобы под знаком радикала не было аргумента функции). Например, 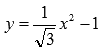  - целая рациональная функция, а не иррациональная. Определение иррациональной функции. Иррациональными называются алгебраические функции, содержащие аргумент под знаком радикала (корня). Примером может являться функция  . ПРИМЕЧАНИЕ: Если вид функции можно упростить на всей области определения, то классификации подлежит именно упрощенная функция. К примеру,   - не иррациональная функция, а рациональная, так как  ;  - не трансцендентная функция, а рациональная алгебраическая, так как  .

Понятие о сложной функции Пусть даны две функции  z = f(y)  и  у = g(x). Сложной функцией (или композицией функций  f  и  g) называется функция z = h(x), значения которой вычисляются по правилу  h(x) = f(g(x))  (т. е. сначала вычисляется g(x), при этом получается некоторое число у, а затем вычисляется значение в точке у).

Пример. Функцию     можно рассматривать как композицию функций     и   .

Для записи композиции функций употребляется значок  . Например, запись    означает, что функция  h  получена как композиция функций  f  и  g (сначала применяется  g, а затем  f), т. е.  . Операция образования сложной функции (или композиция функций) не обладает переместительным свойством:  . Чтобы можно было вычислить сложную функцию  h = f(g(x)), надо, чтобы число  g(x), т. е. значение функции  g, попадало в область определения функции  f .

Пример.  Вычисляя значения функции  , необходимо брать только те числа  х, для которых  , т. е. те, для которых число  попадает в область определения функции  .

2. Взаимно обратные функции Пусть дана функция  у = f(x). Она имеет обратную, если из зависимости  у = f(x)  можно переменную  х  однозначно выразить через переменную  у. Выразив  х через  у, мы получим равенство вида  х = g(y). В этой записи  g  обозначает функцию, обратную к  f. Если функция  g  является обратной для функции  f, то и функция является обратной для функции  g. Пару функций  f  и  g  называют взаимно обратными функциями.

33.

Последовательностью называется множество чисел, перенумерованных с помощью натуральных чисел и расставленных в порядке возрастания их номеров x₁,x₂,...x_n Числа x₁,x₂,...,x_n — называются элементами последовательности, символ x_n — общим элементом, а число n — его номером. Сокращенно последовательность обозначается символом {x_n}.

Счетным множеством называется множество эквивалентное множеству натуральных чисел. Следовательно любая последовательность является счетным множеством.