1.

Системы линейных уравнений: основные понятия

Определение. Система линейных уравнений — это объединение из n линейных уравнений, каждое из которых содержит k переменных. Записывается это так:

Многие, впервые сталкиваясь с высшей алгеброй, ошибочно полагают, что число уравнений обязательно должно совпадать с числом переменных. В школьной алгебре так обычно и бывает, однако для высшей алгебры это, вообще говоря, неверно.

Определение. Решение системы уравнений — это последовательность чисел (k₁,k₂, ..., k_n), которая является решением каждого уравнения системы, т.е. при подстановке в это уравнение вместо переменных x₁, x₂, ..., x_n дает верное числовое равенство.

Соответственно, решить систему уравнений — значит найти множество всех ее решений или доказать, что это множество пусто. Поскольку число уравнений и число неизвестных может не совпадать, возможны три случая:

1. Система несовместна, т.е. множество всех решений пусто. Достаточно редкий случай, который легко обнаруживается независимо от того, каким методом решать систему.

2. Система совместна и определена, т.е. имеет ровно одно решение. Классический вариант, хорошо известный еще со школьной скамьи.

3. Система совместна и не определена, т.е. имеет бесконечно много решений. Это самый жесткий вариант. Недостаточно указать, что «система имеет бесконечное множество решений» — надо описать, как устроено это множество.

Определение. Переменная x_i называется разрешенной, если она входит только в одно уравнение системы, причем с коэффициентом 1. Другими словами, в остальных уравнениях коэффициент при переменной x_i должен быть равен нулю.

Если в каждом уравнении выбрать по одной разрешенной переменной, получим набор разрешенных переменных для всей системы уравнений. Сама система, записанная в таком виде, тоже будет называться разрешенной. Вообще говоря, одну и ту же исходную систему можно свести к разным разрешенным, однако сейчас нас это не волнует. Вот примеры разрешенных систем:

Обе системы являются разрешенными относительно переменных x₁, x₃ и x₄. Впрочем, с тем же успехом можно утверждать, что вторая система — разрешенная относительно x₁, x₃ и x₅. Достаточно переписать самое последнее уравнение в видеx₅ = x₄.

Теперь рассмотрим более общий случай. Пусть всего у нас k переменных, из которыхr являются разрешенными. Тогда возможны два случая:

1. Число разрешенных переменных r равно общему числу переменных k: r = k. Получаем систему из k уравнений, в которых r = k разрешенных переменных. Такая система является совместной и определенной, т.к. x₁ = b₁, x₂ = b₂, ..., x_k = b_k;

2. Число разрешенных переменных r меньше общего числа переменных k: r < k. Остальные (k − r) переменных называются свободными — они могут принимать любые значения, из которых легко вычисляются разрешенные переменные.

Так, в приведенных выше системах переменные x₂, x₅, x₆ (для первой системы) и x₂, x₅(для второй) являются свободными. Случай, когда есть свободные переменные, лучше сформулировать в виде теоремы:

Теорема. Если в системе из n уравнений переменные x₁, x₂, ..., x_r — разрешенные, а x_r + 1, x_r + 2, ..., x_k — свободные, то:

1. Если задать значения свободным переменным (x_r + 1 = t_r + 1, x_r + 2 = t_r + 2, ..., x_k = t_k), а затем найти значения x₁, x₂, ..., x_r, получим одно из решений.

2. Если в двух решениях значения свободных переменных совпадают, то значения разрешенных переменных тоже совпадают, т.е. решения равны.

В чем смысл этой теоремы? Чтобы получить все решения разрешенной системы уравнений, достаточно выделить свободные переменные. Затем, присваивая свободным переменным разные значения, будем получать готовые решения. Вот и все — таким образом можно получить все решения системы. Других решений не существует.

Вывод: разрешенная система уравнений всегда совместна. Если число уравнений в разрешенной системе равно числу переменных, система будет определенной, если меньше — неопределенной.

15. Выражение видаλ₁*A₁+λ₂*A₂+...+λ_n*A_n называется линейной комбинацией векторов A₁, A₂,...,A_n с коэффициентами λ_1, λ₂,...,λ_n.

Определение линейной зависимости системы векторов

Система векторов A₁, A₂,...,A_n называется линейно зависимой, если существует ненулевой набор чисел λ_1, λ₂,...,λ_n,при котором линейная комбинация векторов λ₁*A₁+λ₂*A₂+...+λ_n*A_n равна нулевому вектору, то есть система уравнений: A₁x₁+A₂x₂+...+A_nx_n =Θ имеет ненулевое решение. Набор чисел λ_1, λ₂,...,λ_n является ненулевым, если хотя бы одно из чисел λ_1, λ₂,...,λ_n отлично от нуля.

Определение линейной независимости системы векторов

Система векторов A₁, A₂,...,A_n называется линейно независимой, если линейная комбинация этих векторовλ₁*A₁+λ₂*A₂+...+λ_n*A_n равна нулевому вектору только при нулевом наборе чисел λ_1, λ₂,...,λ_n, то есть система уравнений: A₁x₁+A₂x₂+...+A_nx_n =Θ имеет единственное нулевое решение.

Пример 29.1

Проверить, является ли линейно зависимой система векторов

Решение:

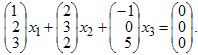
1. Составляем систему уравнений:

2. Решаем ее методом Гаусса. Преобразования Жордано системы приведены в таблице 29.1. При расчете правые части системы не записываются так как они равны нулю и при преобразованиях Жордана не изменяются.

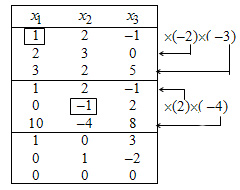
3. Из последних трех строк таблицы записываем разрешенную систему, равносильную исходной системе:

4. Получаем общее решение системы:

5. Задав по своему усмотрению значение свободной переменной x₃ =1, получаем частное ненулевое решение X=(-3,2,1).

Ответ: Таким образом, при ненулевом наборе чисел (-3,2,1) линейная комбинация векторов равняется нулевому вектору -3A₁+2A₂+1A₃=Θ. Следовательно, система векторов линейно зависимая.