2.2.Закрытая и открытая модели

Вернемся к модели (2.1)—(2.3) и подробнее рассмотрим действие основных ограничений (2.2) для ингредиентов различного вида: конечных продуктов, ресурсов, промежуточных продуктов. Для этого дополнительно введем следующие обозначения:

1. — множество индексов ингредиентов (ieI), (I= I^I 2^ I3);

2. — множество индексов ингредиентов, являющихся конечными продуктами ( /^ I);

12. — множество индексов ингредиентов, являющихся ресурсами ( I2^ I), ( I1 n I2=0 );

13. — множество индексов ингредиентов, являющихся промежуточными продуктами ( !з^ I), (

^I3 ⁿ h=0 X ^{( I}3 ^{n I}2=0 ⁾;

S — множество индексов всех технологических способов (seS), (S= Si ^ S 2 ^ Sj);

Sjj — множество индексов технологических способов, в которых промежуточный продукт вида i выпускается, ( Sn ^ S);

Si2 — множество индексов технологических способов, в которых промежуточный продукт вида i расходуется, (S_i2 ^ S), ( Sn n S_i2=0 );

S^ — множество индексов технологических способов, в которых промежуточный продукт вида i не участвует, (S_i3 ^ S), ( S_i3 n Su=0 ), ( S_i3 n S_i2=0 ).

С учетом этих дополнительно введенных обозначений распишем основные ограничения (2.2).

Для конечных продуктов получим запись

Z a_ls Xs > bi (ieIO,

seS

где a_is > 0 и Ь_; >0 , и которая обозначает, что суммарный выпуск i-го конечного продукта во всех технологических способах s должен быть не меньше заданного количества b_i .

Для ресурсов, предположив, что все величины ais и bi опять положительны (как и в предыдущих моделях, т.е. внеся знак “минус” в саму запись), получим, что основные ограничения

2. изменят свой вид и будут выглядеть так

-Z ai_S x_s >-bi (ieh)

se S

или

Z ais Xs < bi (ieI2).

se S

Это указывает на то, что совокупное использование i-го ресурса не может быть больше, чем наличное количество bi .

Для промежуточных продуктов запись ограничений (2.2) будет развернута следующим образом:

£ aisXs + £ aisXs + £ aisXs >bi ⁽ieI 3).

seSil seSi2 s=Si3

С учетом того, что для seS,3 нормы участия a_js =0, а для всех промежуточных продуктов b,=0, имеем

£ aisXs + £ aisXs >0 ⁽ieI 3Х

seSil seSi2

Нулевая правая часть означает как отсутствие заданий на выпуск промежуточной продукции, так и отсутствие ее запасов и поступлений со стороны.

Представив, что все a_is опять привычно положительны, получим следующую запись:

£ aisXs - £ aisXs >0 ^{(i eI} ₃⁾.

seSil seSi2

При равенстве величин суммарного выпуска и общего расхода ограничение выполняется как строгое равенство. При превышении выпуска над расходом возникает некоторый излишек промежуточной продукции сравнительно с собственными нуждами. Он может быть использован либо на продажу, либо как запас (здесь мы выходим за рамки планируемого периода деятельности предприятия). И в том, и в другом случае i-й промежуточный продукт частично приобретает характер конечного продукта.

Для смешанных случаев, когда часть объема какого-либо ингредиента может как получаться со стороны в качестве ресурса, так и отправляться на сторону в качестве конечного продукта, предположив, что все a_js >0, запись ограничений (2.2) преобразуется следующим образом:

£ aisXs > £ aisXs + bi ^(ieI) ,

seSil seSi2

где величины b_i показывают заданные размеры обмена с внешней средой по каждому из ингредиентов i (следовательно, bi могут принимать положительные, отрицательные и нулевые значения).

При превышении расхода i-го ингредиента над его выпуском величины Ь, принимают отрицательные значения, являясь наличным объемом ресурса, поступившего со стороны. При равенстве расхода и выпуска величины bi становятся нулевыми (случай промежуточного продукта в чистом виде).

Что же будет иметь место в случае превышения суммарного расхода i-го ингредиента над его общим выпуском одновременно с нулевым значением величины bi (с отсутствием заранее заданных размеров обмена с внешней средой)? C экономической точки зрения, это будет означать гипотетический план производства, который может быть реализован лишь при дополнительном поступлении данного ингредиента со стороны в размере этого превышения. Будет это поступление, будет возможен и данный вариант. Если же такое поступление со стороны произвести невозможно, то и нереализуем и данный вариант.

В рамках модели (2.1)—(2.3) возникновение подобного случая невозможно, ибо она является закрытой, ввиду жесткой фиксации размеров обмена с внешней средой, т.е. величин b, . Иное дело при использовании открытой модели для той же задачи, где известные величины b_i заменяются на переменные у, . Тогда открытая модель запишется так:

Г

Ё xj=bj ^(j=^1,2,. .,ⁿ⁾ 12

yi>0 (i =1,2,...,m) . 19

ZZ4x5 +y, = bi (i=1,2,...,m) ; 20

_s ⁽j=^1,2,...,ⁿ⁾; 20

Zxj > bj ⁽j=¹,²,...,ⁿ⁾ 20

У>0 (i=1,2,...,m) ; 21

tj >0 ; t,■ >0 ; Tj >0. 32

£ cijTij ^min . 32

^(s = ^1,2,...,^r); 40

(xi - ai) (x2 - a2) < bi , 44

где в зависимости от соотношения расхода и выпуска каждого ингредиента внутри нашего объекта определяется , в каких размерах требуется данный ингредиент реализовать на сторону (как конечный продукт), закупить со стороны (как ресурс) или же ни того, ни другого не требуется (промежуточная продукция).Таким образом, в открытой модели определяются значения переменных величин yi (размеры обмена с внешней средой). И, наоборот, в зависимости от выгодности или невыгодности (с точки зрения критерия оптимальности) тех или иных значений yi

определяются и величины интенсивности x_s. В открытой модели априорное разделение ингредиентов на конечную продукцию, ресурсы и промежуточную продукцию невозможно.

В случае использования в открытой модели критерия оптимальности в форме максимума прибыли ее количество будет зависеть как от размеров выручки от реализации, зависящей в свою очередь от объемов выпуска конечной продукции, так и от затрат, зависящих в свою очередь от размеров закупки ресурсов со стороны и интенсивностей работы технологических способов.

Обозначим:

p_i — цена i -го ингредиента.

Тогда критерий оптимальности закрытой задачи, оставаясь по своему экономическому смыслу максимумом прибыли, запишется иначе, нежели (2.2), а именно:

m

£ p_i y_i ^ max.

Ингредиенты с нулевыми значениями y_i (чистая промежуточная продукция) на величину прибыли не влияют. Так как все цены положительны (p_i >0), то, в силу наличия и положительных и отрицательных значений y_i , прибыль будет определяться как разность между выручкой от реализации и затратами. Однако такая запись критерия оптимальности справедлива только при исчерпывающем описании в открытой модели всех реально существующих ингредиентов.

Всеобъемлющее представление в задаче всех возможных ресурсов как источников затрат практически невозможно, да и нецелесообразно. Этап моделирования (причем не обязательно математического моделирования) неизбежно предполагает абстрагирование от несущественных и агрегирование представления второстепенных особенностей и сторон моделируемого объекта. Целесообразно часть затрат представлять в критерии пропорционально объему закупок соответствующих ингредиентов, а остальные затраты включать в критерий агрегированно, связав их с технологическим способом, т.е. пропорционально интенсивности его использования. Если ввести c_s — затраты в s-ом технологическом способе при его использовании с единичной интенсивностью, то критерий оптимальности открытой модели основной планово­производственной задачи Канторовича будет выглядеть следующим образом:

m r

£ p_i y_i - £ c_s x_s ^ max.

i = 1 s = 1

Если представить, что решение открытой задачи получено и значение величин y_i известно, то известно и сложившееся в данном варианте распределение всех ингредиентов по категориям: конечная продукция, ресурсы, промежуточная продукция; иными словами, распределение всех индексов i по множествам Ii, I2 и I3 . Тогда, представив уже известные величины y_i как неотрицательные, получим следующее экономически прозрачное выражение, описывающее полученную прибыль:

r

£ Р₍Уг -( £ РгУг + £c_sx _s),

1. е/1 i е/ 2 s=1

где первая сумма есть ни что иное как выручка от реализации, а в круглых скобках представлены совокупные затраты.

На основе закрытой и открытой моделей можно сконструировать и некий гибридный вариант. Однако для этого необходимо обязательно вернуться к исходному предположению, что для решения задачи все ингредиенты жестко разделены на конечную продукцию, ресурсы и промежуточную продукцию.

Модель гибридной задачи будет выглядеть так:

r

£ p_s x_s ^ max,

s = 1

r

£ a_u Xs > bi + yi‘ (i = 1,2,...,m);

S = 1

Xs >0

^(s = ^1,2,...,^r);

где yi ’ — принимающие любые значения переменные величины, показывающие дополнительные (по сравнению с заранее заданными величинами bi ) размеры выпуска конечной продукции (или промежуточной продукции в смешанных случаях), либо поступления ресурсов (или промежуточной продукции) со стороны.

Кроме того, следует отметить, что любая из описанных выше моделей основной планово­производственной задачи при необходимости может быть дополнена ограничениями вида

as< Xs< as 0=l,²,...^,rX

где as и as — соответственно минимально и максимально возможные значения интенсивности использования s-го техноло­гического способа; величины as и as могут быть и нулевыми в случае отсутствия необходимости учета нижней и (или) верхней границ использования той или иной технологии.

3. Условия применения линейных моделей при описании функционирования производственных систем

После описания ряда конкретных моделей и их обобщения в основной планово­производственной задаче Канторовича целесообразно рассмотреть некоторые теоретические проблемы описания функционирования производственных систем.

Известно, что для описания процесса функционирования производственной системы используется метод производственных функций.

Пусть, как и выше в процессе производства система использует т видов ресурсов и пусть

вектор b = ⁽ b1,..., bm⁾ e R^m характеризует данный набор используемых ресурсов. В свою очередь, производственная система включает определенный набор технологических способов производства: Т1,..., Т_г , при этом по s-му способу выпускается продукция s-го наименования, в производстве которой используются все виды ресурсов или только некоторая их часть. Производственная функция связывает объем потребляемых по s-й технологии ресурсов с величиной выпуска валовой (в натуральных единицах) или товарной (в стоимостном выражении) продукции s-го наименования.

Таким образом, хs = ^f_s⁽ bi,..., bm⁾ , где x_s — объем продукции, выпускаемой по s-й

технологии, f — соответствующая производственная функция (ПФ).

Если математическая сущность ПФ заключается в том, что она задает отображение множества

наборов ресурсов R ^ R + на множество товарных выпусков R +, то экономическая сущность

ПФ заключается в том, что соотношение х s = ^f_s⁽ ft,. ., bm⁾ выражает объем продукции,

выпущенной по s-й технологии, при наиболее рациональном использовании ресурсов. Основной целью функционирования системы управления производством является выбор вектора ресурсов

be R , а также способа реализации технологии T_s , при котором будет реализован

“оптимальный” способ использования ресурсов.

Производственная функция является одним из основных инструментов планово­производственных расчетов при анализе производственно-коммерческой деятельности промышленной фирмы. Как будет ясно из дальнейшего, ПФ объектов микроэкономики могут быть как линейными, так и (очень часто) нелинейными.

Рассмотрим очень важный для модельных приложений случай, когда технологическое множество производственной системы является линейным выпуклым множеством. В этом случае модель производства оказывается линейной.

Основная предпосылка возможного применения этой модели состоит в том, что любой происходящий производственный процесс можно представить в виде линейной комбинации с неотрицательными коэффициентами некоторых основных (или базовых) производственных процессов. В свою очередь, каждый из этих процессов задается при помощи вектора “выпуск- затраты”, размерность которого определяется суммой количества видов производимых продуктов и потребляемых ресурсов. Коэффициенты в разложении данного производственного процесса по базовым производственным процессам назовем, как и выше, интенсивностями основных способов.

Одним из примеров, характеризующих сказанное, является интерпретация основного производственного способа как производства продукции и расхода ресурсов в единицу времени. В этом случае величины интенсивностей выражают собой, например, количество смен работы некоторого производственного участка по какой-либо из Г технологий. В этом случае основные показатели выпуска продукции и затрат ресурсов на всем производстве являются суммой выпусков и затрат отдельных участков. Последнее и служит основой для представления модели производства как линейной.

Дадим теперь строгие предположения относительно множества технологий Т1,..., Т_Г , которые приводят к линейным моделям.

Предположение 2.1 (об однородности технологических способов или закон постоянства удельного выпуска независимо от масштаба производства):

если (x _s, b) e T _s, то для всякого а > 0 справедливо (aXs, ab) eT_s.

Это предположение означает, что если технологически допустимым является вектор ( x_s , b), то технологически допустимы также векторы “выпуск-затраты”, у которых выпуск увеличивается (уменьшается) в а раз при одновременном увеличении (уменьшении) затрат также в а раз. Предположение 2.2 (об аддитивности технологических способов):

если (х s, b) eT^, а (х _s2, b) ^GT₅₂, то существует такая технология Т, для которой

^(х s ^{+ X} S₂^, bl + b2^{) e}T .

Это предположение означает, что, если возможен выпуск продукции sj-го наименования в количестве х _si при затратах вектора ресурсов bl, а также выпуск продукции 5₂-го наименования в

количестве х _s2 при затратах вектора ресурсов b, то допустимым является выпуск вектора

х s + х _s2 при затратах ресурсов bl + fe .

Предположение 2.3 (о линейной структуре множества технологий):

существует конечное число основных технологических способов (каждый из которых является вектором “выпуск-затраты”): Р1,..., Рк таких, что для любого технологически допустимого набора

(x_s,b) eT_s, найдутся такие неотрицательные числа ^1,..., /Зк, что справедливо соотношение

_ к

(х s, b) = £ 3k Pk.

k=l

Замечание. Совместно предположения 2.1 и 2.2 означают, что технологическое множество является выпуклым конусом. Предположение 2.3, выделяющее линейные технологии, означает,

ту m+К

что этот конус является выпуклым многогранником в полупространстве R + .

Таким образом, в качестве основного параметра линейной производственной системы можно принять вектор основных производственных способов Р1,..., Рк . При этом характеристикой внутреннего состояния системы следует считать неотрицательный вектор их интенсивностей

3= (Л,...,3к). Вектор p, описывающий функционирование всего производства, имеет вид

_ к

(Xs, b) = £3kPk.

k=l

При помощи ограничений на компоненты вектора p формируются производственные и ресурсные ограничения на множества допустимых значений интенсивностей основных технологических процессов. Кроме того, каждая производственная система обладает специфическими ограничениями на интенсивности отдельных технологических способов, обусловленными особенностями производства.

На множестве возможных состояний формируется некоторое правило выбора наилучшего или оптимального состояния производственной системы. Наиболее часто это правило имеет содержательный смысл выпуска наибольшего количества продукции, максимального увеличения прибыли или минимизации затрат. Иногда это правило формулируется путем постановки задачи многоцелевой оптимизации.

Итак, мы рассмотрели связи, существующие между производственными функциями и основной планово-производственной задачей Канторовича, являющейся обобщением линейных оптимизационных задач. Не случайно наиболее общие из встречающихся в литературе многочисленных определений производственной функции не противоречат по своей сути содержанию оптимизационных задач, а определение множества производственных возможностей, как множества всех возможных сочетаний затрат и выпусков, корреспондирует с определением области допустимых планов. При этом мы оставались в рамках наиболее простого с математической стороны случая линейности всех исследуемых зависимостей, т.е. в рамках предпосылки о пропорциональности затрат выпускам и наоборот.

Представим себе любую линейную оптимизационную задачу и кратко напомним основные особенности симплекс-метода. Его идея состоит в переходе от одного базисного (опорного) плана к другому таким образом, что линейная форма улучшается на каждом шаге и достигает экстремума. Переход происходит по вершинам выпуклого многогранника условий в «-мерном пространстве, причем на каждом шаге переход осуществляется в соседнюю вершину. При нахождении в такой вершине проводится проверка плана на оптимальность. Линейная форма (гиперплоскость) делит всё пространство на две части. Вершинам, находящимся в верхней части, соответствуют отрицательные элементы целевой строки, а вершинам из нижней части — положительные. Переход осуществляется только в соседние вершины из верхнего полупространства до тех пор пока в нем не останется ни одной вершины. Переход проводится в ту вершину, которой соответствует максимальный по абсолютной величине из отрицательных элементов целевой строки. Если на последнем шаге линейная форма имеет более одной общей точки с выпуклым многогранником условий, то имеется множество оптимальных планов. Итак, отличительной особенностью метода является движение к оптимуму по вершинам. Все отмеченные выше особенности можно проследить на рис.2.1, где представлен многогранник условий OABCD и показаны положения линейной формы при последовательном движении по вершинам О, А и В (точка оптимума).

На данном рисунке хорошо видно, что для задач линейного программирования характерно следующее:

Рис 2.1

1. Множество допустимых решений выпукло и имеет конечное число крайних точек (вершин);

2. Целевая функция представляет собой гиперплоскость. Гиперплоскости, соответствующие разным значениям целевой функции параллельны.

3. Локальный оптимум является одновременно и глобальным оптимумом.

4. Если целевая функция ограничена на множестве допустимых решений, то оптимум достигается по крайней мере в одной из крайних точек вершин) этого множества, и, начав с произвольной вершины, перемещаясь затем на каждом шаге в соседнюю, достигаем точки оптимума за конечное число шагов.

В задачах нелинейного программирования эти условия полностью или частично не соблюдаются. Рассмотрим ряд случаев.

Случай 1. Пусть при линейных ограничениях имеем нелинейную, сепарабельную целевую функцию вида

2 2 c_i (xi- xi°) + с₂ (х₂- х₂°) ^ min ,

которая экономически представляет собой штраф за отклонение нашего решения от

рекомендованного (желательного). Причем, благодаря возведению в квадрат, одинаково

штрафуются отклонения искомых значений выпусков xi и x2 в любую сторону от их заданных

значений xi° и Х2°. Штрафные коэффициенты с и С2 определяют силу штрафа. Как видим из

рис.1.2 , различным значениям целевой функции соответствуют эллипсы с центрами в точке

(xi°, Х2°), а оптимум достигается в точке А, точке касания эллипсом границы выпуклого

множества допустимых

x2

-V- °

^xi

Рис 2.2

решений.

Итак, в данном случае невыполнение условия 2 влечет за собой и невыполнение условия 4. Оптимум достигается не на вершине, а на грани, откуда следует, что перебор вершин недостаточен.

Из рис. 2.2 видно, что при смягчении заданий по выпуску продукции xi° и Х2° можно

уменьшить сумму штрафа вплоть до нуля. Так, сместив центр эллипса вовнутрь многогранника

условий, получим, что оптимум достигается во внутренней точке.

Случай 2. При иной конфигурации области допустимых значений, описываемой как и ранее

линейными ограничениями, и при опять-таки нелинейной сепарабельной целевой функции вида

2 2 pi (xi- xi°) + Р2 (x2- x2°) ^ max ,

получим рис.2.3. Данная целевая функция экономически представляет собой премию за отклонения выпусков xi и x2 от зара-

нее заданных их значений xi° и x2°, где значения коэффициентов pi и р2 определят силу таких премий. Как видим из рис.2.3, при расположении центра эллипсов внутри многогранника условий в точке Е с координатами xi° и x2° возможно попадание в локальный оптимум в вершине А. Перемещение из нее в соседние вершины В или D ухудшит значение целевой функции (уменьшит эллипс), хотя в вершине С достигается глобальный оптимум. Итак невыполнение условия 2 ведет и к невыполнению условия 3.

Случай 3.Пусть одно из ограничений будут нелинейным, а именно:

(xi - ai) (x2 - a2) < bi ,

где Xi и Х2 — искомые выпуски двух видов продукции, а\ и а2 — минимально разрешенные (по технологическим или экономическим соображениям) размеры производства, a bi — предельно допустимый уровень загрязнения окружающей среды, мультипликативно зависящий от объемов производства двух видов продукции. Кроме того, имеются обычные ограничения по производственной программе и на неотрицательность переменных

Xi + X2 > b2 ;

Xi > 0 ; X2 > 0 .

На рис. 2.4 заштриховяня область допустимых решений. Как

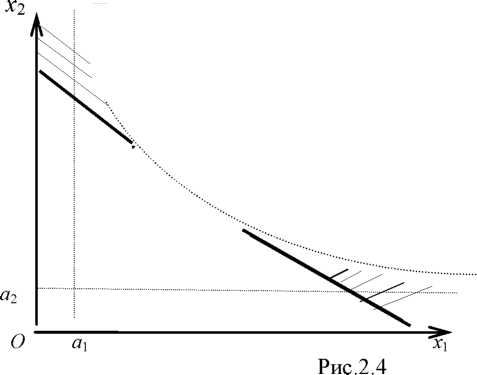
видим, она состоит из двух несвязанных областей. Более того, каждое из двух подмножеств допустимых решений невыпукло. В этих условиях даже линейность целевой функции не может гарантировать от локального оптимума.

Итак, невыполнение условия 1 ведет к невыполнению условий 3 и 4.

Случай 4. Требование целочисленности решения даже при наличии прочих линейных ограничений и линейной целевой функции ведет к невыполнению условий 1 и 4. Из рис.2.5 видно, что область допустимых целочисленных значений переменных состоит из четырех точек О, А, D и Е , а оптимум достигается в точке D. Причем это решение не только существенно хуже оптимального решения без условий целочисленности (достигается в точке В), но и не может быть получено путем его округления до ближайших целых чисел (точки А и С).

^X2

Рис.2.5

Рассмотренные случаи не являются исчерпывающими и служат лишь иллюстрацией, из которой видно, что в чисто вычислительном аспекте для нелинейных задач характерны затруднения с получением точного решения, либо из-за попадания в локальный оптимум, либо из- за плохой сходимости вычислительного процесса. Кроме того, методы нелинейного программирования в отличие от линейного не являются универсальными и приспособлены для решения лишь ограниченного круга задач того или иного специального класса, а потому гораздо более чувствительны к размерности задач.

С содержательной же стороны использование линейных зависимостей дает возможность предельно прозрачно экономически интерпретировать не только модели, отдельные математические выражения и входящие в них величины, а также результаты решения, но даже и сами вычислительные процедуры. Подобные свойства линейных моделей делают их весьма удобными с методической точки зрения для усвоения в процессе обучения общих экономических принципов и закономерностей.

В экономической практике и исследованиях вычислительная привлекательность и хорошая интерпретируемость линейных моделей (не обязательно оптимизационных, т.е. моделей в широком смысле) делает целесообразным их применение и в случае линейной аппроксимации с приемлемой погрешностью нелинейных закономерностей, если это не мешает экономическому содержанию задачи.

4. Алгебра симплекс-метода

Последующий материал, посвященный анализу оптимального решения в задаче Канторовича, существенно использует симплекс-процедуру перехода от начального допустимого базисного решения к оптимальному решению. В связи с этим обстоятельством представляется необходимым напомнить табличный метод нахождения оптимального решения в задаче линейного программирования. Среди множества реализаций симплекс-процедуры выберем ту, которая, во- первых, в явном виде разделяет базисные и свободные переменные и позволяет в последней симплекс-таблице выделить так называемую матрицу эффективности, а во-вторых, хорошо приспособлена для решения на ЭВМ.

В качестве примера рассмотрим простейшую модель оптимизации производства по критерию максимума дохода в случае, когда для производства j-й продукции используется один технологический способ производства Tj ( j = 1,2,..., n). Пусть Pj — доход от реализации продукции, изготовляемой однократным применением j-й технологии. Тогда вектор “выпуск- затраты”, описывающий j-й производственный способ имеет вид Pj =( Pj ; aij , a2j ,..., a_ij ,..., a_nj), где aj — затраты i-го ресурса ( i =1,2,..., т) при однократном применении j-й технологии. Будем считать, что затраты исчисляются в стоимостном выражении. Таким образом, каждая компонента вектора Pj суть стоимость или затрачиваемых производственных факторов, или произведенной продукции.

Состояние производственной системы задается вектором х = ⁽хь . ^ х п⁾ интенсивностей использования технологий Т1,..., Т_п.

Вектор “выпуск-затраты”, описывающий функционирование производственной системы, имеет

_ п п

вид p = £P jX j . При этом выпуск товарной продукции равен £^p,Xj, а затраты i-го ресурса

j=l j=l

n

составляют величину £ aij х j .

j=l

Если целью функционирования производственной системы является максимизация выпуска товарной продукции, то модель производственной системы представляется в следующем виде:

n

Ё xj=bj ^(j=^1,2,. .,ⁿ⁾ 12

yi>0 (i =1,2,...,m) . 19

ZZ4x5 +y, = bi (i=1,2,...,m) ; 20

_s ⁽j=^1,2,...,ⁿ⁾; 20

Zxj > bj ⁽j=¹,²,...,ⁿ⁾ 20

У>0 (i=1,2,...,m) ; 21

tj >0 ; t,■ >0 ; Tj >0. 32

£ cijTij ^min . 32

^(s = ^1,2,...,^r); 40

(xi - ai) (x2 - a2) < bi , 44

Задача нахождения оптимального состояния производственной системы в данном случае является задачей линейного программирования.

1. / 0 0 0\

Пусть x — ⁽Xi,x2, • • •,Xn) — одно из решений задачи линейного программирования. В этом

случае наибольшая величина выпуска определяется числом ^{p —} ЕPjX°- .

j—1

Для нахождения оптимального решения x в задаче (2.7)-(2.9) приведем систему ограничений модели к каноническому виду. Для этого ограничения (2.8), (2.9) превратим в уравнения, введя переменные t_i > 0, экономический смысл которых — количество неиспользованных ресурсов вида

1. :

n

Е aijXj + t_i =b_i (i=l,2,..., m). (2.10)

j—i

Задача линейного программирования (2.7), (2.10), (2.9) с дополнительными ограничениями на неотрицательность переменных ti имеет размерность n + m. При этом число базисных переменных в случае линейной независимости системы ограничений (2.8) равно числу ограничений, т.е. m, а число свободных переменных совпадает с числом неизвестных в линейной форме (2.7), т.е. равно n. Обозначим через с значение целевой функции в форме (2.7).

¹ = 0 - Е ^(_pJ) x j ^ max; j—1

В исходном опорном плане задачи будем считать переменные группы t_i базисными переменными, а группы Xj — свободными. Выразив целевую функцию и базисные переменные через свободные, сформулируем задачу линейного программирования (2.7),(2.10), (2.9) в следующем виде:

n

(2.11) (i=1,2,..., m); (2.12)

ti = bi - Е aij Xj , ti > 0 j—i

Xj > 0 (/=1,2,..., n). (2.9)

(2.13)

Задача (2.11), (2.12), (2.9) может быть представлена следующей матрицей коэффициентов при переменных:

	1	X1 •	• XJ •	• X n
с	a00	a01 •	• a0 j ••	• a0 n
ti	аш	an •	• a1 j ••	• a1 n
ti	ai0	а,1	• •• Gj •	•• ain
tm	am 0	am1	••• amj •	• amn

В матрице (2.13) коэффициенты первой строки совпадают с коэффициентами линейной формы

11. : a₀₀ = 0, a₀₁ = -p₁ ,..., a_on = -p_n , а коэффициенты первого столбца — с коэффициентами правых частей ограничений (2.8): a10 = b ,..., a_io = b_i ,..., a_mo = b_m.

По виду коэффициентов матрицы (2.13) легко судить, является ли найденное базисное решение допустимым и, если оно допустимо, то будет ли оптимальным. Действительно, замечая, что столбец коэффициентов a_io , i ^ 0 представляет собой базисное решение, соответствующее базису t1,..., t_m , а строка коэффициентов ao/ , j ^ 0 представляет собой взятые с обратным знаком коэффициенты при свободных переменных в выражении для с, приходим к выводу, что базисное решение, соответствующее базису t1,..., t_m , допустимо если a_io > 0 (в нашем случае это действительно так: ao = b_i > 0). Если, кроме того, ao/ > 0, то это базисное решение является и оптимальным, так как линейная форма (2.11) принимает наибольшее значение, равное a₀₀ , при равенстве нулю свободных переменных (в нашем случае это условие не выполняется, так как все элементы первой строки матрицы (2.13) неположительны). Таким образом, матрица (2.13) соответствует допустимому базисному решению, но не оптимальному.

Итерационную симплекс-процедуру начнем с первой таблицы, представленной коэффициентами матрицы (2.13), где переменные по строкам соответствуют базисным переменным, а по столбцам — свободным.

Среди отрицательных коэффициентов первой строки выделим наибольший по абсолютной величине, а если таких окажется несколько, то любой из них. Пусть этот коэффициент соответствует свободной переменной X j*. Теперь необходимо X j* перевести в базис, заменив в нем некоторую переменную группы t . Определим, какую из базисных переменных следует сделать свободной. Очевидно, ту, которая быстрее обратится в нуль при увеличении X j*. Это

будет та базисная переменная tf, для которой коэффициент в у*-ом столбце a,j* > 0 и отношение

~наименьшее. Столбец и строку, соответствующие свободной переменной Xj* и базисной t,

^аЧ*

отметим в первой (очередной) симплекс-таблице двойными линейками. Последующие преобразования очередное симплекс-таблицы представлены в табл.2.2.

Таблица 2.2

В табл.2.2 в левом верхнем углу каждой клетки находятся коэффициенты aj предыдущей симплекс-таблицы (в нашем случае — первой), а коэффициенты a j которыми мы заполнили нижние углы, соответствуют пересчету коэффициентов матрицы ограничений (2.12) в связи с тем, что мы заменяем базисную переменную tf на свободную X j*.

Коэффициенты a'j получаем по следующим правилам:

1. коэффициент на пересечении отмеченных строки и столбца а',*/ : а',*/ = 1/ а,*/ ;

2. в клетках выделенной строки записываем верхние коэффициенты, умноженные на а',*/ : ^а'П = ^ап • ^а' */ для j = 0,1, ..., j *- 1, j *+ 1,..., n;

3. в клетках выделенного столбца записываем верхние коэффициенты, умноженные на - а' * j*: а’, / = а, / • (-а’?; ) для i = 0,1,..., i *- 1, i *+ 1,..., m;

4. в клетках выделенной строки отмечаем особым способом верхние коэффициенты а,*j (кроме а,*/ ),а в клетках выделенного столбца — нижние коэффициенты а', j* (кроме а',*/);

5. в остальных клетках записываем произведение выделенных особым способом коэффициентов, на пересечении которых стоит данная клетка: а' _tj = а, * j • а', / для i = 0,1,..., i *- ^{1 i} *+ ^..^ m и j = а^..^ j *- ¹ j *+ ^..^ n.

Затем переходим к заполнению таблицы 2.3, которая отличается от табл.2.2 тем, что отмеченная свободная переменная X j^* стала базисной, а отмеченная базисная переменная t ^* стала свободной.

Верхние левые клетки табл.2.3 (новые значения коэффициентов ау) заполняются по следующим правилам:

1. строка и столбец, соответствующие новым базисной (i*-a строка) и свободной ( 7*-й

столбец) переменным, заполняются нижними коэффициентами выделенных строк и столбца

(н) t » (н)

табл.2.2: ^a.*- = ^ai j для j = 0,1,..., n и ^a * ■* = a'i j* для i = 0,1,..., m.

ⁱ J I J

2. в остальные клетки записываются суммы коэффициентов, стоящих в соответствующих

(н)

клетках табл.2.2: ^а. ■ = ai j + a'i j для i = 0,1,..., i *- 1, i *+ 1,..., m ; j = 0,1,..., j *- 1, j *+ 1, ..., n.

Заполненная таким образом табл.2.3 соответствует матрице коэффициентов (2.13) при новом составе базисных и свободных переменных. Отметим попутно, что a 00 > 0, так как a 00 является произведением положительных чисел a_i*₀ (в силу допустимости предыдущего базисного решения) и a' 0 j* (в силу процедуры выбора j* столбца и правила формирования коэффициента

(н)

a'₀ j). Следовательно, aoo > Goo и значение целевой функции с, соответствующее табл.2.3, выше значения, полученного в табл.2.2. Далее вся процедура повторяется до момента, когда на очередном шаге получается оптимальное решение.

В качестве числового примера, иллюстрирующего табличный метод нахождения оптимального решения в задаче линейного программирования рассмотрим производственную систему с линейным технологическим множеством, использующую три основных производственных способа: Р₁ = (1; 2,1), Р₂ = (3; 1,2) и Р₃ = (3; 3,1). Для определенности затрачиваемые факторы будем интерпретировать как “труд” и “капитал”. В этом случае способ Р3 наиболее трудоемкий, а Р2 — капиталоемкий. Предположение о линейности технологического множества определяет в качестве последнего трехгранный конус в пространстве Р³ (“выпуск-затраты”):

Т = {(с, L, K)\ х₁ > 0; х₂ > 0; х₃ > 0; c = х₁ + 3 х₂ + 3 x₃,

L = 2х₁ + х₂ + 3 х₃, К = х₁ + 2х₂ + х₃}.

Модель производственной системы представим в следующем виде: с = х₁ + 3 х₂ + 3 х₃—> тах; (2.14)

2х₁ + х₂ + 3 х₃ < L; (2.15)

х₁ + 2х₂ + х₃ < K; (2.16)

х₁ > 0; х₂ > 0; х₃ > 0. (217)

Пусть объем фактора L равен 8 единицам, а фактора К — 4 единицам. В этом случае, в ходе решения соответствующей оптимизационной задачи осуществляется выбор интенсивностей использования технологических способов Р1, Р2 и Р3, при которых достигается наибольший выпуск товарной продукции при условии использования факторов “труд” и “капитал” в объеме не превосходящем их наличного количества (8,4).

Приведем краткое решение задачи (2.14)-(2.17).

Ограничения (2.15),(2.16) превратим в уравнения, введя переменные t1 > 0, t2 > 0,

экономический смысл которых — количество неиспользованных ресурсов соответственно вида L и К . При этом получим систему ограничений:

2. x1 + X2 + 3 X3 + t1 = 8; (2.18)

X1 + 2X2 + X3 + t2 = 4. (2.19)

Задача (2.14), (2.17), (2.18), (2.19) с дополнительными ограничениями t₁ > 0, t₂ > 0 является задачей линейного программирования размерности 5, у которой число базисных переменных равно 2 (соответствует числу актуальных ограничений), а число свободных переменных равно 3. Принимая X₁ , X₂ и X₃ за свободные переменные, приведем задачу к следующему виду:

Г с = 0 - (-X₁ - 3 x₂ - 3 x₃)—— maX; j t₁ = 8- (2x₁ + x₂ + 3 x₃ ); (2.20)

t₂ = 4x₁ + 2x₂ + x₃; г X1 > 0; X2 > 0; x₃ > 0; t1 > 0; t2 > 0.

Так как решаемая задача — задача на максимум, то соотношения (2.20) показывают, что начальное базисное решение является допустимым, но не оптимальным (коэффициенты при X1 , X2 и X3 в выражении для с не являются неотрицательными числами).

В ходе последовательного преобразования таблиц коэффициентов, используя симплекс- процедуру, получим оптимальное решение задачи (2.14), (2.18), (2.19), (2.17), исходя из начального допустимого решения (2.20).

Таблица 2.4(а)

Табл.2.4(в) дает оптимальное решение задачи, которое находим по столбцу свободных членов: X2°= 0,8; X3⁰ = 2,4; X1⁰ = t1° = h° = 0; с° = 9,6.

Итак, оптимальному состоянию системы соответствует выпуск товарной продукции объемом с° = 9,6. При этом первый производственный способ оказывается неэффективным и

интенсивность его использования равна нулю. Интенсивности второго и третьего способов соответственно 0,8 и 2,4. Производственные факторы используются полностью, так как их остатки в оптимальном плане равны нулю. Рассмотрим случай, когда количество одного из ресурсов (например, К) изменяется, а второго (в данном случае, L) остается прежним. Пусть величина К уменьшилась с 4 ед. до 2 ед.

Приведем последнюю симплекс-таблицу коэффициентов, дающую оптимальное решение задачи в этом случае:

Таблица 2.5

	1	Xl	t 2	X2
с	6	2	3	3
tl	2	-1	-3	-5
Х3	2	1	1	2

Оптимальному состоянию системы соответствует выпуск товарной продукции с ° = 6 (уменьшился на 3,6 ед.) Наряду с первым производственным способом неэффективным оказывается и второй (X2 = 0) — капиталоемкий. Интенсивность третьего производственного способа соответствует наличному объему капитала. При этом неиспользованный остаток фактора “труд” равен 2 (t1=2). Таким образом, фактор К является дефицитным, а фактор L — недефицитным.