56Основные источники ошибок при измерении горизонтальных углов

В одномерном пространстве (на линии) положение точки фиксируется значением одной координаты X, и ошибка положения точки M_p равна средней квадратической ошибке m_x этой координаты. Истинное положение точки может находиться в интервале ( X - t * m_x ) - ( X + t * m_x ), то-есть, в обе стороны от значения X; на практике коэффициент t обычно задают равным 2.0 или 2.50.

В двумерном пространстве (на поверхности) положение точки фиксируется значениями двух координат, и ошибка положения точки должна задаваться двумя величинами: направлением и ошибкой положения по этому направлению. Геометрическая фигура, внутри которой находится истинное положение точки, может иметь разную форму; в частном случае, когда ошибка положения точки по всем направлениям одинакова, получается круг радиуса R = M_p.

Положение точки по двум измерениям получается в пересечении двух линий положения. Для измеренного расстояния S линией положения является окружность радиуса S с центром в исходной пункте A (рис.2.12а); для измеренного угла β с вершиной в исходном пункте A - прямая линия, проведенная под углом β к исходной линии AB (рис.2.12б).

Вследствие ошибок измерений необходимо ввести понятие "полоса положения". Для расстояния S, измеренного со средней квадратической ошибкой m_s - это круговой пояс (кольцо) шириной 2 * m_s между двумя окружностями радиусами ( S - m_s ) и ( S + m_s ); для угла β, измеренного с ошибкой m_β - это узкий треугольник с вершиной в точке A и углом при вершине 2 * m_β. Линия положения точки является осью симметрии полосы положения (рис.2.12).

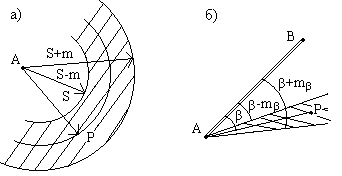
Рис.2.12. Линия положения и "полоса положения" точки P: а) для измеренного расстояния, б) для измеренного угла.

Систематические ошибки имеют определенный источник, направление и величину. Если источник систематической ошибки обнаружен и изучен, то можно получить формулу влияния этой ошибки на результат измерения и затем ввести в него поправку; это исключит влияние систематической ошибки. Пока источник какой-либо систематической ошибки не найден, приходится считать ее случайной ошибкой, ухудшающей качество измерений.

Случайные ошибки измерений обусловлены точностью способа измерений (строгостью теории), точностью измерительного прибора, квалификацией исполнителя и влиянием внешних условий. Закономерности случайных ошибок проявляются в массе, то-есть, при большом количестве измерений; такие закономерности называют статистическими. Освободить результат единичного измерения от случайных ошибок невозможно; невозможно также предсказать случайную ошибку единичного измерения. Теория ошибок занимается в основном изучением случайных ошибок.

Другие источники ошибок:

- приборные ошибки;

- геометрии наблюдений;

- точности моделей, используемых при обработке результатов: математических, физических, геофизических.

57Метод тригонометрического нивелирования

Тригонометрическое нивелирование называют также геодезическим или нивелированием наклонным лучом. Оно выполняется теодолитом; для определения превышения между двумя точками нужно измерить угол наклона и расстояние. В точке А устанавливают теодолит, в точке В - рейку или веху известной высоты V. Измеряют угол наклона зрительной трубы теодолита при наведении ее на верх вехи или рейки (рис.4.38). Длину отрезка LK можно представить как сумму отрезков LC и CK с одной стороны и как сумму отрезков LB и BK с другой. Отрезок LC найдем из ΔJLC: LC = S*tg ν , остальные отрезки обозначены на рисунке.

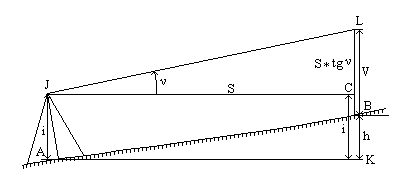
Рис.4.38

Тогда

LC + CK = LB + BK       и      S * tg( ν) + i = V + h.

Отсюда выразим превышение h

h = S * tg(ν) + i - V.                  (4.67)

Выведем формулу превышения из тригонометрического нивелирования с учетом кривизны Земли и рефракции. Вследствие рефракции луч от верхнего конца вехи идет по кривой, а визирная линия трубы будет направлена по касательной к этой кривой в точке J. Визирная линия трубы пересечет продолжение вехи в точке L₁, а не L. Проведем уровенные поверхности в точках A, B, J (рис.4.39).

Проведем касательную к уровенной поверхности в точке J и обозначим: высоту прибора - i, высоту вехи - V, горизонтальное проложение линии AB - S.

Превышение точки B относительно A выражается отрезком BK. Отрезок L₁K на рис.4.39 можно выразить через его части двумя путями:

L₁K = L₁E + EF + FK,

L₁K = L₁L + LB + BK.

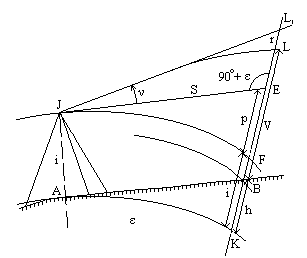
Рис.4.39

Отрезок L₁E найдем из Δ JL₁E. Этот треугольник можно считать прямоугольным, так как угол L₁EJ очень мало отличается от прямого, всего лишь на величину центрального угла ε =(S / R)*r. Этот угол при S = 1 км не превосходит 0.5'.

Итак,

L₁E = JE * tg(ν),

но поскольку JE = S, то L₁E = S * tg(ν).

Отрезок EF выражает влияние кривизны Земли:

EF = p = S² / 2*R;

отрезок FK равен высоте прибора FK = i; отрезок L₁L выражает влияние рефракции:

L₁L = r * (S² / 2*R) * k = p * k;

отрезок LB равен высоте вехи V.

Таким образом,

S * tg(ν) + p + i = r + V + h,

откуда

h = S * tg(ν) + (i - V) + (p - r),

или

h = S * tg(ν) + (i - V) + f.                   (4.68)

При измерении расстояния с помощью нитяного дальномера формула превышения несколько изменяется; так как S = (Cl + c)* Cos²(ν), то

h = 0.5*(Cl + c)*Sin(2*ν) + i - V + f = h'+ i - V + f,

Величину h'= 0.5*(Cl + c)*Sin(2*ν) называют тахеометрическим превышением.

При S = 100 м величиной f можно пренебречь, так как

f = 0.66 мм . S² ,

где S - расстояние (в сотнях метров).

Ошибка измерения превышения из тригонометрического нивелирования оценивается величиной от 2 см до 10 см на 100 м расстояния.

При последовательном измерении превышений получается высотный ход; в высотном ходе углы наклона измеряют дважды: в прямом и обратном направлениях.