Подобие диффузионных процессов

Уравнение конвективной диффузии математически описывает процесс массопереноса в одной фазе и для вывода критериев подобия оно должно быть дополнено соответствующими условиями, характеризующими массообмен на границе раздела фаз.

При одномерном диффузионном потоке в соответствии с 1-м законом Фика к поверхности раздела фаз будет передано количество вещества:

dM = - D dFdτ. По Закону Щукарева: dM = dF ΔC d , отсюда:

- D = .

На основе теории подобия после деления правой части на левую без учета знаков математических операций, замены x на (определяющий размер) получим:

- диффузионный критерий Нуссельта – характеризует массообмен на границе фаз и является аналогом теплового критерия Нуссельта.

Из дифференциального уравнения конвективной диффузии для одномерного случая:

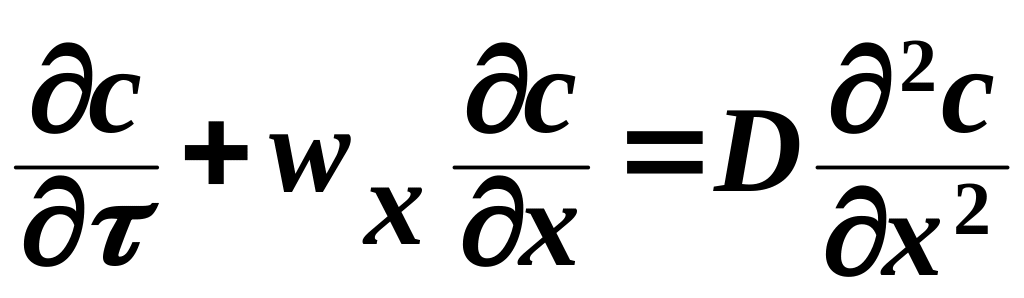путем деления правой части уравнения на 1-ое слагаемое левой части, после преобразований получаем:

- диффузионный критерий Фурье, который характеризует нестационарный диффузионный процесс.

Поделив 2-ое слагаемое левой части на правую, получим:

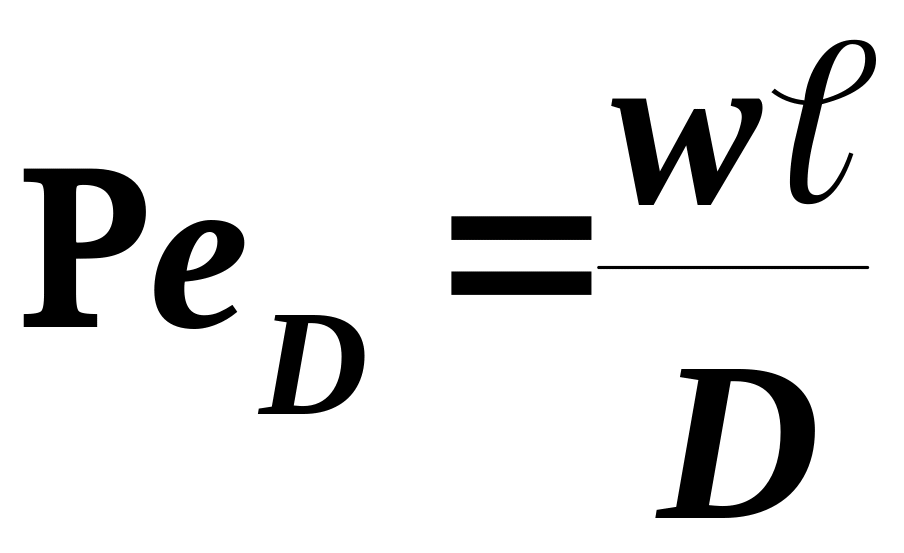- диффузионный критерий Пекле, который характеризует подобие полей концентраций по длине пути.

Гидродинамическое подобие в массообменных аппаратах характеризуется критерием: Re= ; ,

Pr_D- диффузионный критерий Прандтля, характеризует подобие полей физических величин.

Учитывая, что критерий Nu_D является определяемым, общее критериальное уравнение конвективной диффузии записывается следующим образом: .

При вынужденном движении исключается Gr, т.к. естественной конвекцией можно пренебречь, и или .

Для естественной конвекции из общего уравнения выпадает критерий Re: или .

Значения коэффициентов А, m и n определяются исходя из опытных данных для конкретных случаев диффузионных процессов.

Критерий Nu_D вычисляется по полученным критериальным уравнениям и по нему определяют : .

Абсорбция

Абсорбция – процесс поглощения газов или паров из газовой или парогазовой смеси жидким поглотителем.

Поглощаемое вещество – абсорбтив, распределен в инертном газе.

Поглотитель – абсорбент (жидкость).

Процесс – избирательный и обратимый. Различают физическую и химическую абсорбцию. Примеры абсорбции: получение Н₂S0₄, аммиачной воды, чистка отходящих газов.

Равновесие при абсорбции

Условия равновесия – равенство температур и Р обеих фаз и равновесие концентраций для всех компонентов в обеих фазах, которое характеризуется константой фазового равновесия m. В общем случае m=f(P, T, x). В большинстве случаев эта функция находится экспериментально. В системе газ-жидкость - закон Генри ( - парциальное давление газа над раствором, Е – константа Генри, х – концентрация газа в растворе в мольном выражении). Е зависит от природы растворимого газа и температуры. С ростом температуры растворимость газов уменьшается.

Согласно закону Дальтона p= Py; сопоставим и получим ,

. Условия абсорбции улучшаются, если Р - повысить, а температуру снизить.

Материальный баланс абсорбции.

Если принять, что L и G постоянны по высоте аппарата, а концентрации выразить в относительных массовых концентрациях , , то G( ) = L( - ), отсюда ; Обозначим (*), где - удельный расход абсорбента.

(*) – уравнение рабочей линии процесса абсорбции. (*) показывает, что изменение концентрации в абсорбционых аппаратах при L, G = Const по высоте аппарата является линейным. Построим рабочую линию, где

tgα = , т.е. различным удельным расходам абсорбента будут отвечать различные рабочие линии; точки Ai лежат на одной и той же горизонтальной прямой, соответствующей .