11. Оптимальная оценка параметров сигнала при действии нормального белого шума

При действии норм аддитивного БШ U(t,α). После опыта апостериорная плотность распределения вероятностей – симметрична относительно max

Wсш(α/х)

Wсш(х/ α) – функция правдоподобия. Введем вместо ф. правдоподобия – отношение правдоподобий

По критерию max функции правдоподобия запишем критерий max отношения правдоподобий

Где

Поиск max (оптимального параметра α):

Если Э не зависит от α, то оптим. Оценка опред-ся по корреляционному интегралу

КОР. 2

X(t)

Ψ(α_i-1)

Устр. сравн

Ψ(α_i)

КОР. 1

Uon(t,α_i)

Uon(t,α_i-1)

Uon(t,0)

Z

Блок смещения по α

Измерит. α_i

α_i

Один приемник может использоваться для обнаружения и изменения параметра

Сигнальная и шумовая сост. кор. интеграла

Основная функція приемника - вычисление ВКФ между пришедшим сигналом и сигналом уже имеющимся в приемнике

12. Потенциальная точность измерения временного положения сигналов

Р ассмотрим воздействие смеси сигнала и нормального белого шума U1(t)=V1(t)+n1(t) на линейный фильтр с импульсной характеристикой h(t). Вследствие линейности фильтра на его выходе получим аддитивную смесь сигнала с шумом U2(t)=V2(t)+n2(t)

В

Рисунок 1 Временная диаграмма сигнала и смеси сигнала с шумом на выходе фильтра

ременное положение сигнала и, в частности, момент его максимума характеризуют дальность отразившей его цели. Шум искажает сигнал на выходе фильтра (рис. 7.1) и смещает момент его максимума до величины τ, которая и является оценкой вре­менного положения. Разность этой оценки и момента максимума сигнала и составляет погрешность этого измерения: ∆τ = τ–τ0

Как правило, измерение параметров сигнала ведется при достаточно большом от­ношении С/Ш, что и обеспечивает высокую точность этого измерения. При этом предположении погрешность измерения достаточно мала.

Потенциальная точность временного положения сигнала (время прихода):

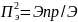где — максимально возможное отношение С/Ш на выходе линейного фильтра, т. е. на выходе оптимальною фильтра; —отношение энергий производной сигнала и самого сигнала.

где G1(w) — амплитудный спектр сигнала U1(t), a

так как производная сигнала U1(t) имеет амплитудный спектр fU1(t). Поэтому

П_э тем больше, чем шире спектр сигнала. Таким образом, потенциальная точность измерения временного положения сигнала тем выше, чем больше отношение С/Ш и эффективная ширина спектра сигнала.

13. Потенциальная точность измерения частоты

Рассматривая запись мгновенного значения простейшего гармонического сигнала U1(t,f)=cos2Пft, замечаем, что в ней частота и время являются равноправными переменными. Смещенный по времени сигнал

U1(t-τ,f)=cos2Пf(t-τ)

записывается аналогично сигналу со смещением по частоте:

U1(t, f—F) = cos2П (f—F)t.

Эта аналогия имеет глубокий физический смысл. К тому же точность измерения временного положения сигнала при заданном отношении С/Ш определяется только основной частотной характеристикой сигнала - его амплитудным спектром S1(f)

Сравнение двух приведенных выше соотношений показывает полную симметричность сигнала относительно времени и частоты. Поэтому все полученные выражения для точности измерения временного положения сигнала справедливы и при измерении частоты, если в этих выражениях поменять местами временные и частотные характеристики. min дисперсия погрешности частоты

где Т_э — эффективная длительность cигнала. Следовательно, потенциальная точность измерения частоты сигнала тем выше, чем больше отношение сигнал-шум и эффективная длительность сигнала.

Заметим, что начало отсчета времени сигналов в формулах (7.12) и (7.13) выбирается из условия

Наилучшей формой для измерения частоты, а следовательно, и радиальной скорости цели обладает сигнал

состоящий из двух дельта-импульсов, которые действуют в моменты времени t1=-t_max и t2=tmax, т. е. разнесены во времени на ∆t=2tmax. Тогда, будучи излученными, они позволяют измерить дальности r1 и r2 цели в два момента времени со сдвигом на ∆t и по этим значениям определить радиальную скорость цели v_r= (r2—r1)/∆t

Однако сигналы такой формы не обеспечивают РС по скорости даже двух целей, находящихся на достаточно близких расстояниях. Действительно, от каждой цели будут отражаться по два импульса. Всего же от двух целей придет четыре одинако­вых по форме коротких импульса. И оказывается принципиально невозможным установить, какие же два импульса соответствуют первой цели, а какие — второй. Для получения высокой РС и однозначности измерения частоты сигнал должен быть непрерывным на всем интервале своего действия.

Оптимальная оценка —при минимуме дисперсии.