7 Согласование уровней сигналов. Сопряжение кмоп и тлл схем.

С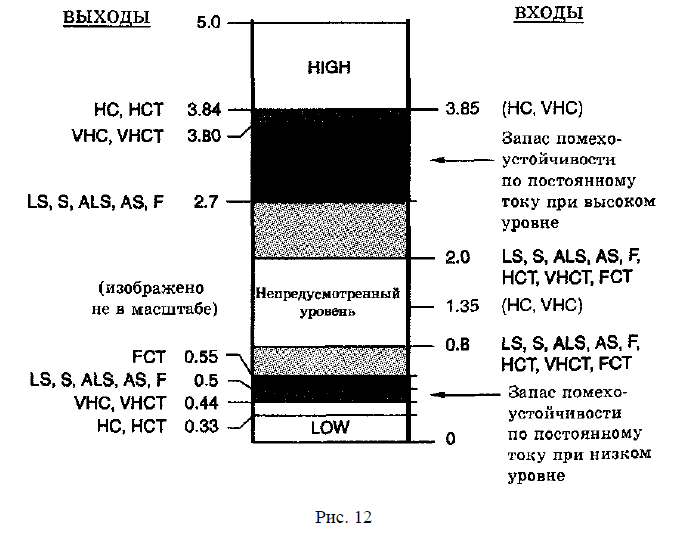 опряжение КМОП- и ТТЛ-схем. При выборе семейства ИС разработчик цифровой аппаратуры по умолчанию руководствуется общими требованиями в отношении быстродействия, потребляемой мощности, стоимости и т.д. Однако в некоторых случаях разработчик может выбирать в качестве элементной базы и разные семейства ИС из-за их доступности или других специальных требований. Таким образом, для разработчика важно понимать, как соединяются выходы ТТЛ-схем с входами КМОП-схем и наоборот. При сопряжении ТТЛ- и КМОП-схем следует учесть несколько факторов. Первый из них – запас помехоустойчивости. Запас помехоустойчивости по постоянному току при низком уровне зависит от напряжения Uвых0max на выходе схемы, являющейся источником сигнала, а также от напряжения Uвх0max для входа, подключенного к данному выходу, и равняется Uвх0max - Uвых0max. Точно так же запас помехоустойчивости по постоянному току при высоком уровне равняется Uвых1min - Uвх1min. На рис. 12 приведены соответствующие значения для КМОП- и ТТЛ-схем.

В качестве следующего фактора рассмотрим коэффициент разветвления по выходу. Как и в случае с «чистыми» ТТЛ-схемами, разработчик должен сложить входные токи устройств, подключенных к выходу, и сравнить результат с возможностями данной схемы по выходу при обоих уровнях выходного сигнала. Если ТТЛ-схема управляет КМОП-схемами, то проблем с коэффициентом разветвления по выходу не возникает, так как входам КМОП- схем при любом уровне сигнала почти не требуется никакого тока. С другой стороны, входам ТТЛ-схем, особенно при низком уровне входного сигнала, требуется значительный ток, по сравнению с возможностями выходных каскадов схем НС и НСТ. Последний фактор – величина емкостной нагрузки. Емкостная нагрузка приводит к увеличению, как задержки, так и мощности, рассеиваемой логической схемой. Изменение задержки особенно заметно у схем НС и НСТ, для которых время переходного процесса растет примерно на 1 нс при увеличении емкости нагрузки на каждые 5 пФ. Транзисторы выходных каскадов схем FCT во включенном состоянии имеют очень малое сопротивление, поэтому для данных схем время переходного процесса растет только на 0,1 нс с увеличением емкости нагрузки на каждые 5 пФ. При заданной емкости нагрузки, напряжении питания и одинаковых условиях эксплуатации, динамическая рассеиваемая мощность у всех КМОП- семейств одна и та же. С другой стороны, динамическая мощность, рассеиваемая в выходных цепях ТТЛ-схем, несколько меньше из-за меньшего перепада напряжения между высоким и низким уровнями у этих схем.

8 Схемы низковольтной кмоп-логики и их сопряжение с другими схемами.

Два важных фактора подтолкнули производителей ИС к снижению напряжения питания КМОП-схем: 1) при снижении напряжения питания динамическая рассеиваемая мощность уменьшается; 2) по мере продвижения технологии ко все меньшим размерам транзисторов, изоляция в виде окиси кремния между затвором КМОП-транзистора и стоком и истоком становится все более тонкой и поэтому неспособна выдержать разность потенциалов, доходящую до 5 В. В результате группой промышленных стандартов ИС Объединенного технического совета по электронным приборам (JEDEC) в качестве стандарта для логических схем были выбраны следующие напряжения питания: 3,3 В ± 0,3 В; 2,5 В ± 0,2 В и 1,8 В ± 0,15 В. Стандартами JEDEC определены также входные и выходные напряжения логических уровней устройств, работающих с этими напряжениями питания.

Переход к меньшим напряжениям происходил постепенно и будет продолжаться дальше. В отношении дискретных логических семейств тенденция состояла в том, чтобы выпускать компоненты с меньшим напряжением питания и с меньшими значениями напряжений на выходах, нодопускающие, тем не менее, более высокие напряжения на входах (например, этот подход позволяет КМОП-схемам с напряжением питания 3,3 В работать совместно с 5-вольтовыми КМОП- и ТТЛ-схемами). Подобный подход использован во многих специализированных интегральных схемах и микропроцессорах, но часто применяется также и другой метод. Упомянутые устройства достаточно велики, так что имеет смысл снабдить их двумя источниками питания. Низкое напряжение, например 2,5 В, служит питанием для внутренних узлов микросхемы, ее логического ядра (core logic). Большее напряжение, например 3,3 В, используется для питания внешних цепей ввода и вывода, образующих интерфейсный блок, посредством которого осуществляется сопряжение со схемами старшего поколения, примененными в системе. Для быстрого и безошибочного преобразования логических уровней между логическим ядром и интерфейсным блоком применяются специальные буферные схемы.

Первым шагом на пути уменьшения напряжения питания КМОП-схем стало напряжение 3,3 В. Фактически стандарт JEDEC для 3,3-вольтовой логики определяет два набора уровней. Уровни LVCMOS (низковольтовые уровни КМОП-схем; low-voltage CMOS) относятся к случаю использования только КМОП-схем, когда выходы схем слабо нагружены по постоянному току (меньше 100 мкА), так что напряжения Uвых0 и Uвых1 отличаются от потенциала земли и от напряжения питания не более, чем на 0,2 В. Уровни LVTTL (низковольтовые уровни схем, совместимых с ТТЛ; low-voltage TTL), приведенные на рис. 13, в, используются в приложениях, где выходы существенно нагружены по постоянному току, и поэтому напряжение Uвых0 может достигать 0,4 В, а напряжение Uвых1 может опускаться до 2,4 В. Таким образом, можно применять в одном устройстве ТТЛ-схемы (с напряжением питания 5 В) и схемы с уровнями LVTTL (с напряжением питания 3,3 В), только следуя следующим трем правилам: 1) сигналы с выходов схем с уровнями LVTTL можно непосредственно подавать на входы ТТЛ-схем при соблюдении обычных ограничений на выходной ток схем, являющихся источниками сигналов; 2) сигналы с выходов ТТЛ-схем можно непосредственно подавать на входы схем с уровнями LVTTL, если последние допускают входные напряжения 5 В; 3) выходы ТТЛ-схем и схем с уровнями LVTTL с тремя состояниями можно подключать к одной и той же шине при условии, что выходы схем с уровнями LVTTL допускают напряжение 5 В.

Переход от 3,3-вольтовых схем к 2,5-вольтовым схемам не так прост. Известно, что выходы 3,3-вольтовых схем можно соединять с входами 2,5- вольтовых схем, если эти входы допускают напряжение 3,3 В. Однако как показывают рис. 13, в и г выходное напряжение Uвых1 2,5-вольтовой схемы равняется входному напряжению Uвх1 3,3-вольтовой схемы. Запас помехоустойчивости по постоянному току при высоком уровне, когда выход 2,5-вольтовой схемы соединен с входом 3,3-вольтовой схемы, равен нулю, что не желательно. Эта проблема решается путем применения преобразователя уровня (level translator) или схемы сдвига уровня (level shifter), т.е. устройства, на которое подаются оба напряжения питания и внутри которого происходит подтягивание более низких логических уровней (соответствующих напряжению питания 2,5 В) до больших значений (соответствующих напряжению питания 3,3 В). Сегодня многие специализированные интегральные схемы и микропроцессоры содержат внутри себя преобразователи уровней, что позволяет логическому ядру работать с напряжением питания 2,5 В или 2,7 В, а интерфейсному блоку – с напряжением питания 3,3 В.