
- •Самостоятельное изучение
- •Модели и система параметров логических элементов
- •2. Типы выходных каскадов цифровых элементов: логический выход.
- •3. Типы выходных каскадов цифровых элементов: выходы с тремя состояниями.
- •Типы выходных каскадов цифровых элементов: выход с открытым коллектором.
- •Паразитные связи цифровых элементов по цепям питания, фильтрация питающих напряжений в схемах цифровых устройств.
- •6 Типовые ситуации при построении цифровых устройств на имс
- •7 Согласование уровней сигналов. Сопряжение кмоп и тлл схем.
- •8 Схемы низковольтной кмоп-логики и их сопряжение с другими схемами.
- •8 Схемы низковольтной кмоп-логики и их сопряжение с другими схемами. (продолжение)
- •9 Элементы индикации
- •9 Элементы индикации (продолжение)
- •10 Риски в комбинационных схемах.
- •11. Дешифраторы, преобразователи кодов
- •12. Шифраторы
- •13. Мультиплексоры.
- •14. Демультиплексоры
- •Компараторы (схемы сравнения).
- •16.Синхронизация в цифровых устройствах.
- •17. Регистры.
- •18. Счетчики. Двоичные счетчики.
- •18. Счетчики. Двоичные счетчики. (продолжение)
- •19. Двоично-кодированные счетчики с произвольным модулем.
- •20. Счетчики с недвоичным кодированием.
- •20. Счетчики с недвоичным кодированием. (продолжение)
- •21. Полиномиальные счетчики.
- •2 1. Полиномиальные счётчики (продолжение)
- •22. Представление чисел с фиксированной запятой.
- •23. Представление чисел с плавающей запятой.
- •24. Погрешности представления чисел.
- •25. Кодирование двоичных чисел со знаком: прямой код
- •26. Кодирование двоичных чисел со знаком: дополнительный код.
- •27. Кодирование двоичных чисел со знаком: обратный код.
- •28. Сложение и вычитание двоичных чисел в форме с фиксированной запятой со знаком в прямых кодах. Особенности выполнения операций над числами без знака.
- •29. Сложение и вычитание двоичных чисел в форме с фиксированной запятой со знаком в дополнительных кодах.
- •30. Сложение и вычитание двоичных чисел в форме с фиксированной запятой со знаком в обратных кодах.
- •30. Сложение и вычитание двоичных чисел в форме с фиксированной запятой со знаком в обратных кодах. (продолжение)
- •31. Переполнение при сложении чисел с фиксированной запятой. Модифицированные коды. [лекции, стр.26-28]
- •31. Переполнение при сложении чисел с фиксированной запятой. Модифицированные коды. [лекции, стр.26-28] (продолжение)
- •32.Умножение чисел с фиксированной запятой: общая схема целочисленного умножения. [подробнее с примерами – лекции, стр. 28-3 , но это след. Вопросы]
- •33. Методы умножения двоичных чисел без знака: умножение с младших разрядов множителя со сдвигом множимого.
- •34. Методы умножения двоичных чисел без знака: умножение с младших разрядов множителя со сдвигом суммы частичных произведений
- •35. Методы умножения двоичных чисел без знака: умножение со старших разрядов множителя со сдвигом множимого.
- •36. Методы умножения двоичных чисел без знака: умножение со старших разрядов множителя со сдвигом суммы частичных произведений.
- •Умножение двоичных чисел со знаком. Умножение чисел в дополнительном коде.
- •38. Логические методы ускорения умножения: алгоритм Бута.
- •39 Логические методы ускорения умножения: модифицированный алгоритм Бута, алгоритм Лемана
- •40. Логические методы ускорения умножения: умножение с обработкой двух разрядов множителя за шаг (умножение на два разряда одновременно)
- •41.Деление чисел с фиксированной запятой: общая схема целочисленного деления.
- •42. Методы деления двоичных чисел без знака: деление с восстановлением остатка.
- •43. Методы деления двоичных чисел без знака: деление без восстановления остатка.
- •44. Деление двоичных чисел со знаком. Деление чисел в дополнительном коде.
- •Сложение и вычитание двоичных чисел в форме с плавающей запятой.
- •46.Умножение чисел с плавающей запятой.
- •47. Деление чисел с плавающей запятой.
- •48.Выполнение операций сложение и вычитание в двоично-десятичном коде.
- •49.Сложение в двоично-десятичном коде чисел со знаком.
- •50.Сумматоры. Одноразрядный сумматор. Многоразрядные сумматоры.
- •50.Сумматоры. Одноразрядный сумматор. Многоразрядные сумматоры. (продолжение)
- •51.Арифметико-логические устройства (алу).
6 Типовые ситуации при построении цифровых устройств на имс
Р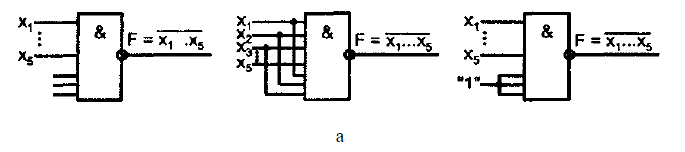
 азработанная
проектировщиком функционально-логическая
схема подлежит далее реализации на
наборе стандартных ИС той или иной серии
или на наборе библиотечных элементов
той или иной БИС/СБИС с программируемой
структурой. В обоих случаях возможны
несовпадения элементов подлежащей
изготовлению схемы и имеющихся для ее
реализации. Типовыми ситуациями являются
наличие у имеющихся элементов лишних
(неиспользуемых в данном случае) входов,
наличие в корпусах ИС лишних элементов
или, напротив, нехватка у имеющихся
элементов необходимого числа входов
или нагрузочной способности. Режимы
неиспользуемых входов.
Вопрос о режиме лишних входов решается
с учетом конкретного типа используемой
схемотехнологии. возможно
поступить следующим образом: не обращать
внимания на лишние входы (т.е. оставить
их неподключенными), подсоединить их к
задействованным входам или подать на
них некоторые константы. С точки зрения
логических операций все три возможности
правомерны (рис. а). Для КМОП и ТТЛ(Ш)
неиспользуемые входы разомкнутыми не
оставляют. Для КМОП это строгая
рекомендация, т.к. у них очень велики
входные сопротивления и, следовательно,
на разомкнутые входы легко наводятся
паразитные потенциалы, которые могут
изменять работу схемы. Для ТТЛ(Ш) строгого
запрета на оставление разомкнутых
входов нет, но это делать незачем, т.к.
вследствие этого пострадают параметры
быстродействия элемента. Подсоединение
лишних входов к задействованным для
КМОП и ТТЛ(Ш) принципиально возможно,
но нежелательно, т.к. оно приводит к
увеличению нагрузки на источник сигнала,
что также сопровождается уменьшением
быстродействия источника сигнала.
Таким образом, для
КМОП и ТТЛ(Ш) режим неиспользуемых входов
– подсоединение их к константам
(логическим единицам или нулям), не
изменяющим работу схемы для задействованных
входов. Режимы
неиспользуемых элементов.
Если не все элементы, имеющиеся в корпусе
ИС, использованы в схеме, то неиспользованные
элементы также подключены к напряжению
питания, которое является общим для
всего корпуса. Если же мощности,
потребляемые элементами в состояниях
нуля и единицы, не равны, то имеет смысл
поставить неиспользуемый элемент в
состояние минимальной мощности, подав
на какой-либо из его входов соответствующую
константу. Наращивание
числа входов.
Для элементов И и ИЛИ это не представляет
трудностей: для получения нужного числа
входов берется несколько элементов,
выходы которых объединяются далее
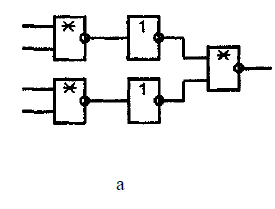
элементом того же типа. Наращивание
числа входов для операций И-НЕ, ИЛИ-НЕ,
в сущности, производится аналогичным
методом, но в схеме появляются
дополнительные инверторы (рис. 11, а). На
этом рисунке звездочка обозначает
операцию Шеффера или Пирса. Снижение
нагрузок на
выходах логических элементов. Это может
понадобиться, если нагрузки превышают
допустимые значения, а также для
повышения
быстродействия схем, на которое нагрузки
элементов оказывают самое непосредственное
влияние. Чем больше число нагрузок у
элемента- источника сигнала (или
нестандартная внешняя нагрузка), тем
большее время тратится на достижение
выходным сигналом порогового уровня
при переключении, т.е. на изменение его
логического состояния. Для предотвращения
потерь быстродействия из-за нагрузок
на выходах сильно нагруженных элементов
применяют буферизацию или разделение
нагрузки Введение
буферных каскадов ускоряет работу
источника сигнала, но вносит собственную
задержку в тракт передачи сигнала.
При разделении
нагрузки новые элементы с задержками
в тракт передачи сигнала не вводятся,
но увеличивается нагрузка на тот источник
сигнала, который формирует сигналы для
рассматриваемой схемы.
азработанная
проектировщиком функционально-логическая
схема подлежит далее реализации на
наборе стандартных ИС той или иной серии
или на наборе библиотечных элементов
той или иной БИС/СБИС с программируемой
структурой. В обоих случаях возможны
несовпадения элементов подлежащей
изготовлению схемы и имеющихся для ее
реализации. Типовыми ситуациями являются
наличие у имеющихся элементов лишних
(неиспользуемых в данном случае) входов,
наличие в корпусах ИС лишних элементов
или, напротив, нехватка у имеющихся
элементов необходимого числа входов
или нагрузочной способности. Режимы
неиспользуемых входов.
Вопрос о режиме лишних входов решается
с учетом конкретного типа используемой
схемотехнологии. возможно
поступить следующим образом: не обращать
внимания на лишние входы (т.е. оставить
их неподключенными), подсоединить их к
задействованным входам или подать на
них некоторые константы. С точки зрения
логических операций все три возможности
правомерны (рис. а). Для КМОП и ТТЛ(Ш)
неиспользуемые входы разомкнутыми не
оставляют. Для КМОП это строгая
рекомендация, т.к. у них очень велики
входные сопротивления и, следовательно,
на разомкнутые входы легко наводятся
паразитные потенциалы, которые могут
изменять работу схемы. Для ТТЛ(Ш) строгого
запрета на оставление разомкнутых
входов нет, но это делать незачем, т.к.
вследствие этого пострадают параметры
быстродействия элемента. Подсоединение
лишних входов к задействованным для
КМОП и ТТЛ(Ш) принципиально возможно,
но нежелательно, т.к. оно приводит к
увеличению нагрузки на источник сигнала,
что также сопровождается уменьшением
быстродействия источника сигнала.
Таким образом, для
КМОП и ТТЛ(Ш) режим неиспользуемых входов
– подсоединение их к константам
(логическим единицам или нулям), не
изменяющим работу схемы для задействованных
входов. Режимы
неиспользуемых элементов.
Если не все элементы, имеющиеся в корпусе
ИС, использованы в схеме, то неиспользованные
элементы также подключены к напряжению
питания, которое является общим для
всего корпуса. Если же мощности,
потребляемые элементами в состояниях
нуля и единицы, не равны, то имеет смысл
поставить неиспользуемый элемент в
состояние минимальной мощности, подав
на какой-либо из его входов соответствующую
константу. Наращивание
числа входов.
Для элементов И и ИЛИ это не представляет
трудностей: для получения нужного числа
входов берется несколько элементов,
выходы которых объединяются далее
элементом того же типа. Наращивание
числа входов для операций И-НЕ, ИЛИ-НЕ,
в сущности, производится аналогичным
методом, но в схеме появляются
дополнительные инверторы (рис. 11, а). На
этом рисунке звездочка обозначает
операцию Шеффера или Пирса. Снижение
нагрузок на
выходах логических элементов. Это может
понадобиться, если нагрузки превышают
допустимые значения, а также для
повышения
быстродействия схем, на которое нагрузки
элементов оказывают самое непосредственное
влияние. Чем больше число нагрузок у
элемента- источника сигнала (или
нестандартная внешняя нагрузка), тем
большее время тратится на достижение
выходным сигналом порогового уровня
при переключении, т.е. на изменение его
логического состояния. Для предотвращения
потерь быстродействия из-за нагрузок
на выходах сильно нагруженных элементов
применяют буферизацию или разделение
нагрузки Введение
буферных каскадов ускоряет работу
источника сигнала, но вносит собственную
задержку в тракт передачи сигнала.
При разделении
нагрузки новые элементы с задержками
в тракт передачи сигнала не вводятся,
но увеличивается нагрузка на тот источник
сигнала, который формирует сигналы для
рассматриваемой схемы.
