41.Деление чисел с фиксированной запятой: общая схема целочисленного деления.

Деление несколько более сложная операция, чем умножение, но базируется на техже принципах. Основу составляет общепринятый способ деления с помощью операций вычитания или сложения и сдвига.

Деление выражается как последовательность вычитаний делителя сначала из делимого, а затем из образующихся в процессе деления частичных остатков. Реализовать деление можно двумя основными способами:

- с неподвижным делимым и сдвигаемым вправо делителем;

- с неподвижным делителем и сдвигаемым влево делимым.

Недостатком первого способа является потребность иметь в устройстве деления сумматор и регистр двойной длины. Второй способ позволяет строить делитель с сумматором одинарной длины. Неподвижный делитель D хранится в регистре одинарной длины, а делимое Z, сдвигаемое относительно D, находится в двух таких же регистрах. Образующиеся цифры частного Q заносятся в освобождающиеся при сдвиге Z разряды одного из регистров Z.

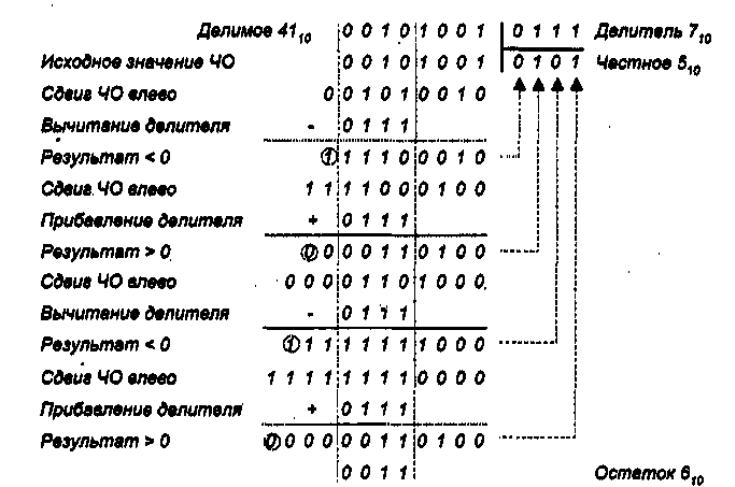
42. Методы деления двоичных чисел без знака: деление с восстановлением остатка.

Наиболее очевидный алгоритм носит название алгоритма деления с неподвижным делителем и восстановлением остатка. В учебнике он представлен в силу того, что очень похож на общепринятый способ деления столбиком. Данный алгоритм может быть описан следующим образом:

1. Исходное значение частичного остатка полагается равным старшим разрядам делимого.

2. Частичный остаток удваивается путем сдвига на один разряд влево. При этом в освобождающийся при сдвиге младший разряд 40 заносится очередная цифра частного.

3. Из сдвинутого Ч0 вычитается делитель и анализируется знак результата вычитания.

4. Очередная цифра модуля частного равна единице, когда результат вычитания положителен, и нулю, если отрицателен. В последнем случае значение остатка восстанавливается до того значения, которое было до вычитания.

5. Пункты 2-4 последовательно выполняются для получения всех цифр модуля частного.

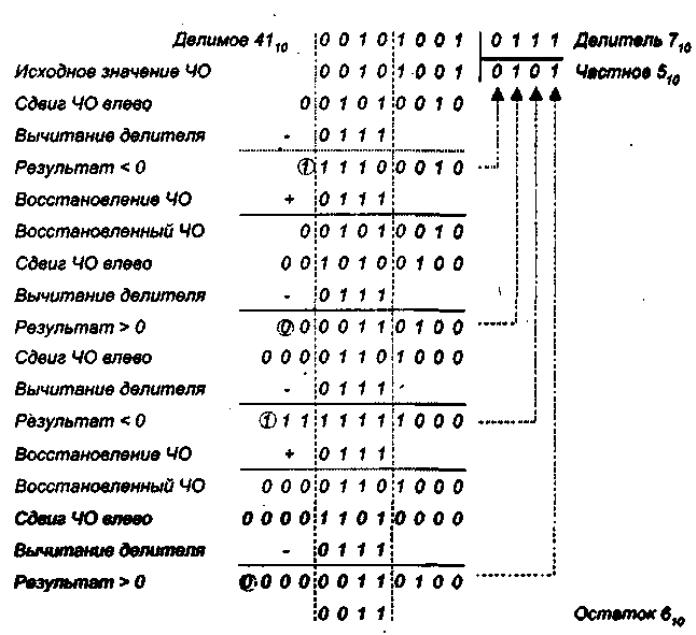
43. Методы деления двоичных чисел без знака: деление без восстановления остатка.

Недостаток затронутого алгоритма заключается в необходимости выполнения на отдельных шагах дополнительных операций сложения для восстановления частичного остатка. Это увеличивает время выполнения деления, которое в этом случае может меняться в зависимости от конкретного сочетания кодов операндов.

В силу указанных причин реальные делители строятся на основе алгоритма деления с неподвижным делителем без восстановления остатка. Приведем описание этого алгоритма.

1, Исходное значение частичного остатка полагается равным старшим разрядам делимого.

2, Частичный остаток удваивается путем сдвига на один разряд влево. При этом в освобождающийся при сдвиге младший разрядЧ0 заносится очередная цифра частного.

3, Из сдвинутого частичного остатка вычитается делитель, если остаток положителен, и к сдвинутому частичному остатку прибавляется делитель, если остаток отрицательный.

4. Очередная цифра модуля частного равна единице, когда результат вычитания положителен, и нулю, если он отрицателен.

5. Пункты 2-4 последовательно выполняются для получения всех цифр модуля частного.

Как видим, пункты 1,2,5 полностью совпадают с соответствующими пунктами предыдущего алгоритма деления.