31. Переполнение при сложении чисел с фиксированной запятой. Модифицированные коды. [лекции, стр.26-28] (продолжение)

Решение: а)

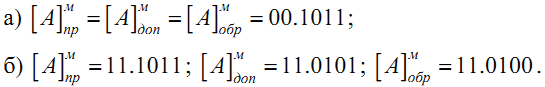
Сложение чисел в модифицированных кодах сводится также к их арифметическому сложению, при этом оба знаковых разряда участвуют в сложении наравне со значащими. В дополнительном модифицированном коде единица переноса из старшего знакового разряда суммы теряется, а в обратном модифицированном – прибавляется к младшему разряду суммы.

П ример. Сложить два отрицательных числа в модифицированных дополнительных кодах: A = -1 1 , B = -11 1, n = 4.

Решение. [A]доп = 11. 11 ; [B]доп = 11. 11

Комбинация 1 указывает на переполнение 

32.Умножение чисел с фиксированной запятой: общая схема целочисленного умножения. [подробнее с примерами – лекции, стр. 28-3 , но это след. Вопросы]

Используемая в ЭВС схема умножения похожа на известную из школьного курса процедуру умножения «в столбик». Вычисление произведения P (p_2n-1р_2n-2 … p₁p ) двух n-разрядных двоичных чисел без знака A (a_n-1a_n-2 … а₁а ) и В (b_n-1b_n-2 … b₁b ) сводится к формированию частичных произведений (ЧП) Wi по одному на каждую цифру множителя, с последующим суммированием полученных ЧП. Перед суммированием каждое частичное произведение должно быть сдвинуто на один разряд относительно предыдущего согласно весу цифры множителя, которой это ЧП соответствует.

Поскольку сомножителями являются двоичные числа, вычисление ЧП упрощается – если цифра множителя bi, равна , то Wi, тоже равно , а при bi = 1 частичное произведение равно множимому (Wi = А). Перемножение двух n-разрядных двоичных чисел Р = А × В приводит к получению результата, содержащего 2n разрядов. Таким образом, алгоритм умножения предполагает последовательное выполнение двух операций – сложения и сдвига.

Суммирование ЧП обычно производится не на завершающем этапе, а по мере их получения. Это позволяет избежать необходимости хранения всех ЧП, то есть сокращает аппаратные затраты. Процесс получения произведения включает умножение множимого (Мн) А на каждую цифру bi множителя (Мт) В. Получаемые при этом частичные произведения Wi = Abi последовательно складываются (накапливаются), образуя суммы частичных произведений (частичные суммы) СЧП. Последняя сумма частичных произведений равна полному произведению.

Таким образом, процесс умножения n-разрядного двоичного множимого А на n-разрядный двоичный множитель В состоит из повторяющейся n раз последовательности умножения А на каждую очередную цифру В. Такая последовательность называется циклом умножения. На каждом цикле умножения сначала определяется очередное ЧПi, далее ЧПi, прибавляется к СЧПi-1, в результате чего определяется очередная сумма частичных произведений СЧПi, и так до получения СЧПn.

Для правильного накопления сумм частичных произведений в каждом цикле умножения множимое (очередное частичное произведение) должно сдвигаться влево (при умножении с младших разрядов множителя) или вправо (при умножении со старших разрядов множителя), при этом сумма частичных произведений должна быть неподвижна. Правильное накопление сумм частичных произведений будет происходить также в случае, если множимое (очередное частичное произведение) на каждом цикле умножения добавлять в одни и те же разряды, т.е. сделать его неподвижным, а после каждого очередного суммирования сдвигать очередную сумму частичных произведений вправо (при умножении с младших разрядов множителя) или влево (при умножении со старших разрядов множителя).

Таким образом, возможны четыре варианта реализации схемы умножения (метода умножения). Методы умножения двоичных беззнаковых чисел основаны на представлении произведения в виде полинома.

1. Умножение, начиная с младших разрядов множителя, при сдвиге множимого влево и неподвижной сумме частичных произведений.

2. Умножение, начиная со старших разрядов множителя, при сдвиге суммы частичных произведений влево и неподвижном множимом.

3. Умножение, начиная со старших разрядов множителя, со сдвигом множимого вправо и при неподвижной сумме частичных произведений.

4. Умножение, начиная с младших разрядов множителя, со сдвигом суммы частичных произведений вправо и при неподвижном множимом.