26. Кодирование двоичных чисел со знаком: дополнительный код.

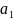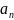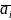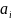Дополнительный код числа А=-0, … – такое машинное изображение этого числа =1, … , для которого =0, если =1, и =1, если =0, за исключением последнего значащего разряда, для которого =1 при =1.

Например, число А=-0,101110 запишется в дополнительном коде так: =1,010010.

Дополнительный код является математическим дополнением до основания системы счисления: |A|+ =q, где |A| - абсолютное значение числа А.

Так как положительные числа не меняют своего изображения в дополнительном коде, то правила преобразования в дополнительный код можно записать следующим образом: =

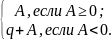
Максимальное дополнительное число, представляемое при этом, равно 1- .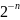

Наибольшее отрицательное число, которое можно записать в дополнительном коде, определим следующим образом. Предположим, что наибольшее отрицательное число А´=-0,11…11. Тогда изображение этого числа в дополнительном коде 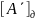=1,00…01. Если к числу А´ добавить единицу в самый младший разряд, то в результате получим число -1,00…0. Преобразовав это число по формальным правилам, получим 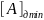=1,00…0.

Следовательно, диапазон изменения машинных изображений чисел для формы представления с запятой, фиксированной перед старшим разрядом, в дополнительном коде будет -1≤ ≤(1- ).

Как отмечалось ранее, для ЕС ЭВМ машинные изображения чисел – всегда целые числа. При этом наибольшее положительное число состоит из целой части, все разряды которой равны единице, и знакового разряда, равного нулю (например, в случае 16 двоичных разрядов (два байта) максимальное положительное число имеет вид 0111111111111111, т.е. равно 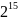-1); наибольшее отрицательное число состоит из целой части, все разряды которой равны нулю, и знакового разряда, равного единице, т.е. имеет вид 1000000000000000. В этом случае говорят о форме представления чисел с фиксированной точкой. Таким образом, соотношение для представления целых чисел в дополнительном коде принимает следующий вид: |A|+ =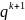 , где k – количество разрядов в целой части машинного изображения числа (k= ).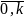

27. Кодирование двоичных чисел со знаком: обратный код.

Обратный код числа А=-0, … – такое машинное изображение этого числа 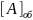=1, … , для которого =0, если =1, и =1, если =0.

Из определения следует, что обратный код двоичного числа является инверсным изображением самого числа, в котором все разряды исходного числа принимают инверсное (обратное) значение, т.е. все нули заменяют на единицы, а все единицы – на нули, например если А=-0,101110, то =1,010001.

Следовательно, для обратного кода чисел, представленных в форме с запятой, фиксированной перед старшим разрядом, справедливо соотношение: |A|+ =q- , где |A| - абсолютная величина числа А; n – количество разрядов после запятой в изображении числа.

Правила преобразования чисел в обратный код можно сформулировать следующим образом:

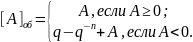
Сравнив формулы, видим, что = + .

Это соотношение используют для получения дополнительного кода отрицательных чисел следующим образом: сначала инвертируется цифровая часть исходного числа, в результате получается его обратный код; затем добавляется единица в младший разряд цифровой части числа и тем самым получается дополнительный код этого изображения.

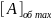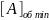В обратном коде можно изображать максимальное положительное число =0,111…1=1- и наибольшее отрицательное число =-0,111…1=-(1- ), записываемое в виде 1,000…0.

При проектировании цифровых автоматов необходимо учитывать неоднозначность изображения нуля в обратном коде:

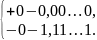
Использование различных способов изображения отрицательных чисел в цифровом автомате обуславливает целый ряд особенностей выполнения операций алгебраического сложения двоичных чисел.