24. Погрешности представления чисел.

!!!!Уважаемый читатель, знай, все указанные в тексте и на рисунках точки и запятые не случайны! Они нужны для правильного ответа!

Представление числовой информации в ЭВС, как правило, влечет за собой появление погрешностей (ошибок), величина которых зависит от формы представления чисел и от длины разрядной сетки.

Абсолютная погрешность представления – разность между истинным значением исходной величины А и ее значением, полученным из машинного изображения А_М, т.е. Δ[A]=A−A_M .

Относительная погрешность представления – величина

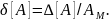
Все числа целого типа переводятся из одной системы счисления в другую точно (без погрешностей). Операции сложения, вычитания и умножения чисел целого типа также выполняются точно. Результат деления чисел целого типа дает целое частное и целый остаток.

Правильные дроби переводятся из одной системы счисления в другую не точно – с погрешностью. Поэтому для чисел с фиксированной запятой погрешность представления имеет место только в случае правильных дробей.

Абсолютная погрешность перевода десятичной дроби в систему с основанием r при использовании усечения (младшие цифры справа отбрасываются) определяется следующим выражением:

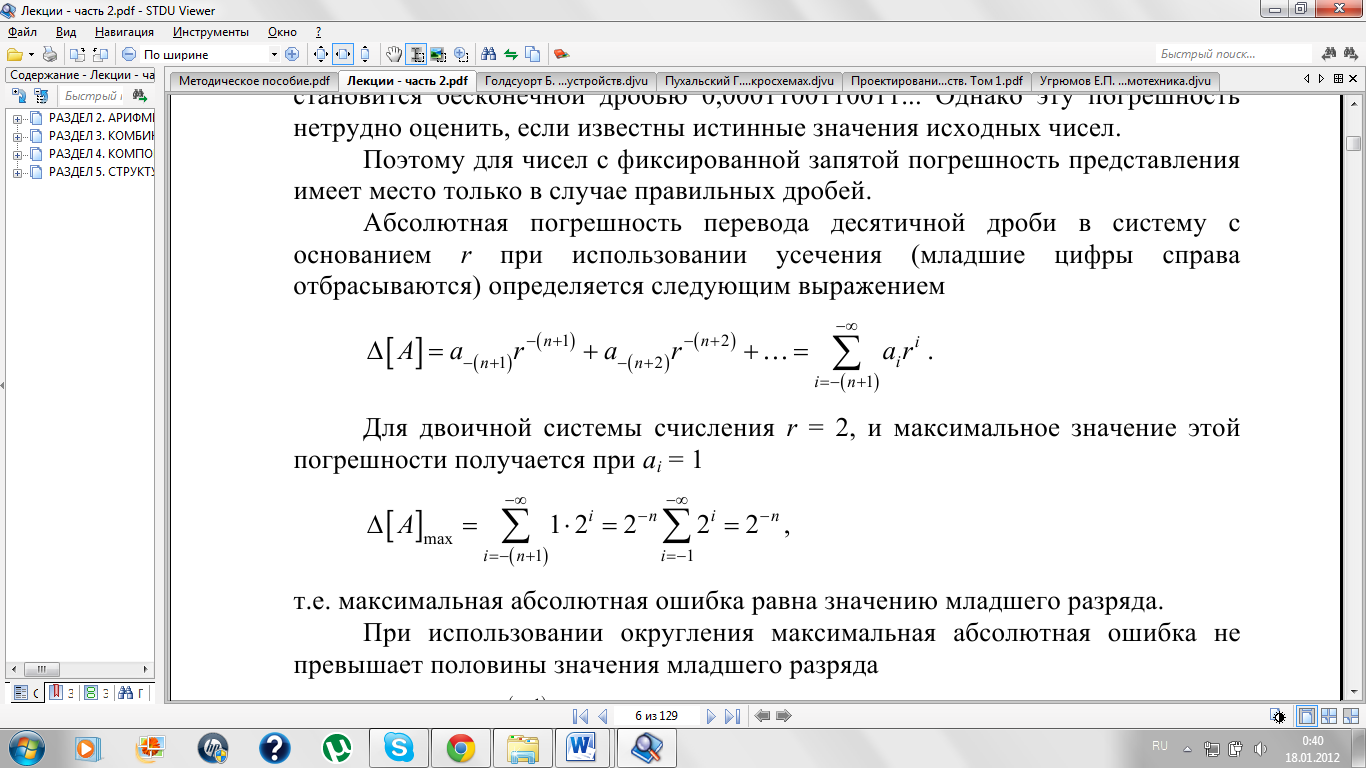
Для двоичной системы счисления r = 2, и максимальное значение этой погрешности получается при a_i = 1:

т.е. максимальная абсолютная ошибка равна значению младшего разряда.

При использовании округления максимальная абсолютная ошибка не превышает половины значения младшего разряда Δ [A]_max=2⁻⁽ⁿ⁺¹⁾=0,5 ⋅2⁻ⁿ .

Для представления чисел в форме с фиксированной запятой абсолютное значение машинного изображения правильной дроби находится в диапазоне 2^-n ≤ |A|_Ф ≤ 1 - 2^-n.

Следовательно, относительная погрешность представления для максимального значения числа равна

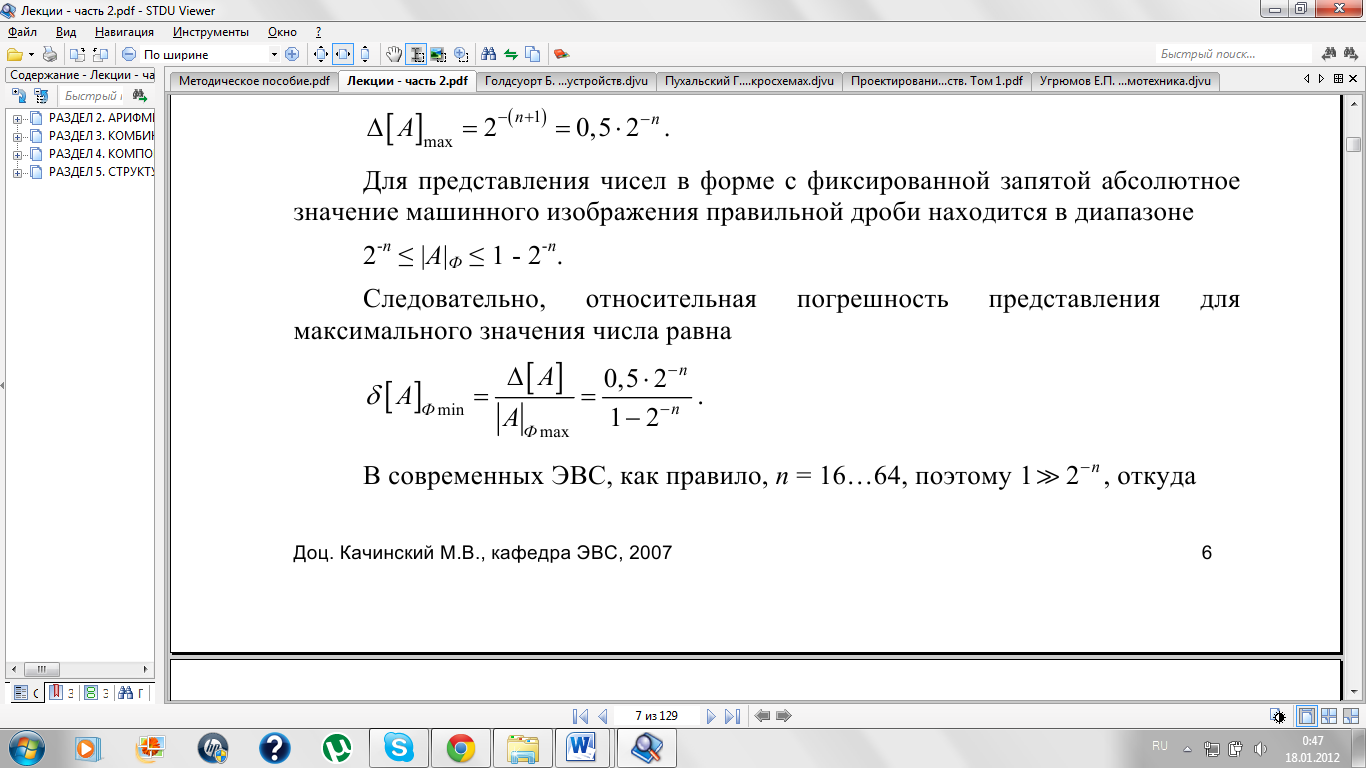
В современных ЭВС, как правило, n = 16…64, поэтому 1>> 2^-n, откуда δ[A]_{Ф min} =0,5 ⋅2^-n .

Аналогично, для минимального значения: 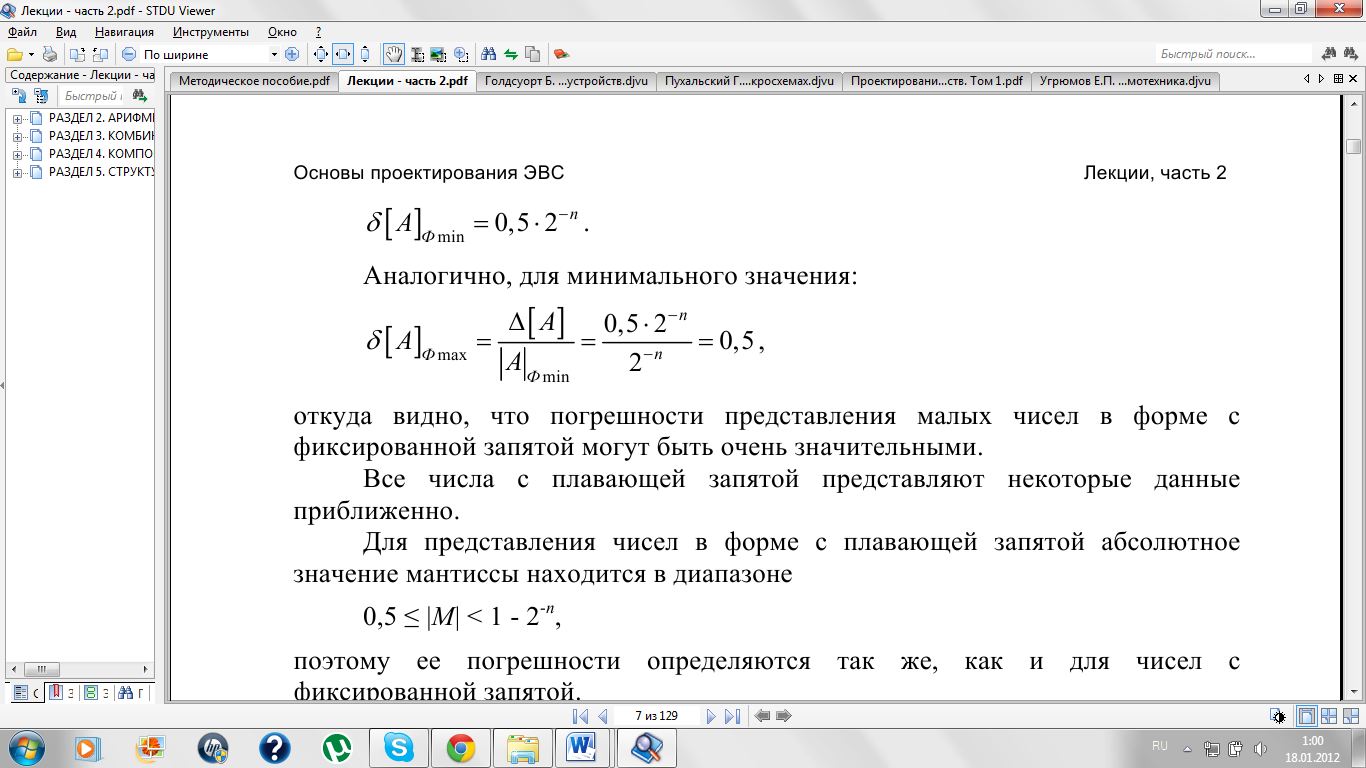откуда видно, что погрешности представления малых чисел в форме с фиксированной запятой могут быть очень значительными.

Все числа с плавающей запятой представляют некоторые данные приближенно.

Для представления чисел в форме с плавающей запятой абсолютное значение мантиссы находится в диапазоне 0,5 ≤ |M| < 1 - 2^-n, поэтому ее погрешности определяются так же, как и для чисел с фиксированной запятой.

Для нахождения погрешностей представления чисел в форме с плавающей запятой величину этой погрешности надо умножить на величину 2^pA :

Из полученных выражений следует, что максимальная абсолютная ошибка не превышает половины значения младшего разряда мантиссы с учетом порядка, а относительная точность представления чисел в форме с плавающей запятой почти не зависит от величины числа.

25. Кодирование двоичных чисел со знаком: прямой код

Прямой код

Прямой код – это представление числа в двоичной системе счисления, при котором первый (старший) разряд отводится под знак числа. Если число положительное, то в левый разряд записывается 0; если число отрицательное, то в левый разряд записывается 1.

Таким образом, в двоичной системе счисления, используя прямой код, в восьмиразрядной ячейке (байте) можно записать семиразрядное число. Например:

0 00011010 - положительное число

1 00011010 – отрицательное число

Количество значений, которые можно поместить в семиразрядной ячейке со знаком в дополнительном разряде равно 256. Это совпадает с количеством значений, которые можно поместить в восьмиразрядную ячейку без указания знака. Однако диапазон значений уже другой, ему принадлежат значения от -128 до 127 включительно (при переводе в десятичную систему счисления).

При этом в вычислительной технике прямой код используется почти исключительно для представления положительных чисел.

Для отрицательных чисел используется так называемый дополнительный код. Это связано с удобством выполнения операций над числами электронными устройствами компьютера.

Операция сложения положительного числа и отрицательного числа, представленного в прямом коде

Прямой код числа 5: 0 000 0101

Прямой код числа -7: 1 000 0111

Два исходных числа сравниваются. В разряд знака результата записывается знак большего исходного числа.

Если числа имеют разные знаки, то вместо операции сложения используется операция вычитания из большего по модулю значения меньшего. При этом первый (знаковый) разряд в операции не участвует.

_ 000 0111

000 0101

-------------

000 0010

После выполнения операции учитывается первый разряд.

Результат операции 1 000 0010, или -210.