2 1. Полиномиальные счётчики (продолжение)

Рассмотрим схему счетчика при s = 3 (рис. 10.7):

В данном случае D-триггер и сумматор по модулю два в его обратной связи представляют собой T-триггер. Поэтому эту схему можно преобразовать следующим образом (рис. 10.8), и она может быть построена только на D- и T-триггерах, соединенных в кольцо (рис. 10.9).

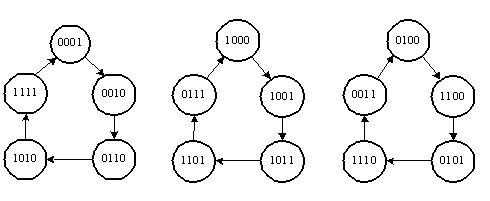
З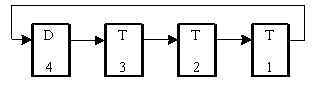 десь необходимо отметить, что для того, чтобы каждый выходной разряд счетчика также формировал последовательности максимальной длины, необходимо, чтобы число шагов s и период последовательности M были взаимно простыми числами, т.е. (M, s) = 1. Поскольку в данном примере это условие не выполняется, диаграмма последовательности состояний регистра разбивается на несколько периодов меньшей длины

Пусть s = 4. Матрица в этом случае имеет вид:

Э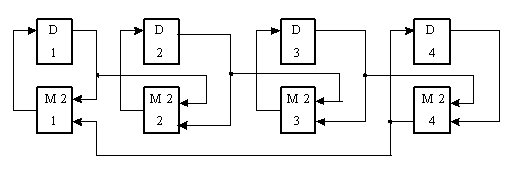 та схема может быть построена только на Т-триггерах и одном сумматоре по модулю два (рис. 10.12):

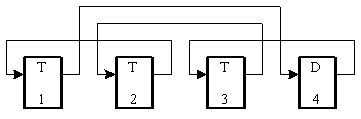
В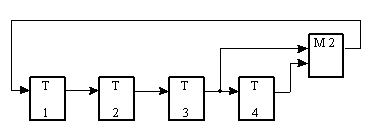 общем случае схема полиномиального счетчика на основе n-разрядного регистра сдвига с линейными обратными связями представлена на рис. 10.13:

с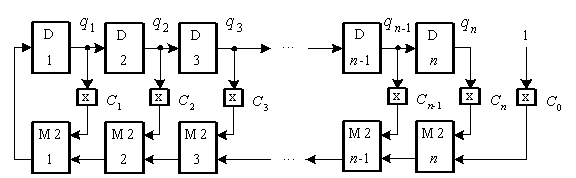 ли коэффициент C_i = 1, то выход i-го триггера подается на вход сумматора по модулю 2, если же C_i = 0, то – не подается. В соответствии с коэффициентами многочлена однозначно определяется структура обратной связи регистра сдвига. Есть таблица всех неприводимых многочленов, из которой находят многочлены, представленные в 8-ричной форме.

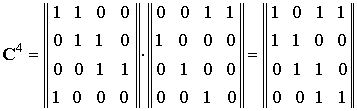
Например, характеристический многочлен   = x⁴   x   1 в этой таблице будет иметь следующий вид:

 =   .

В двоичном виде этом многочлен запишется как: 10 011, или в 8-ричном виде – 23. По такой записи многочлена однозначно строится схема полиномиального счетчика.

22. Представление чисел с фиксированной запятой.

!!!!Уважаемый читатель, знай, все указанные в тексте и на рисунках точки и запятые не случайны! Они нужны для правильного ответа!

В ЭВС числа и нечисловая информация представляются совокупностью двоичных разрядов. Совокупность двоичных разрядов, предназначенных для представления (записи) данных, называется разрядной сеткой.

В ЭВС применяют две формы представления чисел: с фиксированной запятой (точкой) и с плавающей запятой (точкой). Эти формы называют также соответственно естественной и нормальной.

При естественной форме число записывается в естественном натуральном виде с выделением в общем случае следующих компонент числа: знака, запятой и цифр числа. Для сокращения длины разрядной сетки и упрощения обработки данных в конкретных ЭВС положение запятой фиксируется схемотехнически, т.е. аппаратными средствами. Такая форма представления числа называется формой с фиксированной запятой. Такое название связано с тем, что запятая, отделяющая дробную часть от целой, фиксируется в определенном месте относительно разрядов числа. При этом в слове данных сохраняются только два структурных компонента: один знаковый разряд и n разрядов для представления цифр числа. Для кода знака обычно выделяется крайний слева разряд. В знаковом разряде 1 соответствует минусу, а 0 – плюсу. Обычно положение запятой фиксируется либо после младшего (0 разряда), либо перед старшим, (n-1) разрядом. В первом случае числа представлены как целые, во втором – как правильные дроби. При этом запятая никак не обозначается, но в алгоритмах выполнения операций (умножение, деление) ее место учтено заранее одним из указанных способов.

В случае целых чисел минимальным по модулю отличным от нуля числом будет Аmin = 00…01, = 1, а максимальным, которому соответствуют единицы во всех n разрядах, – Amах = 11…11, = 2ⁿ - 1, т. е. диапазон представления чисел в этом случае 1 ≤ |A| ≤ 2ⁿ - 1.

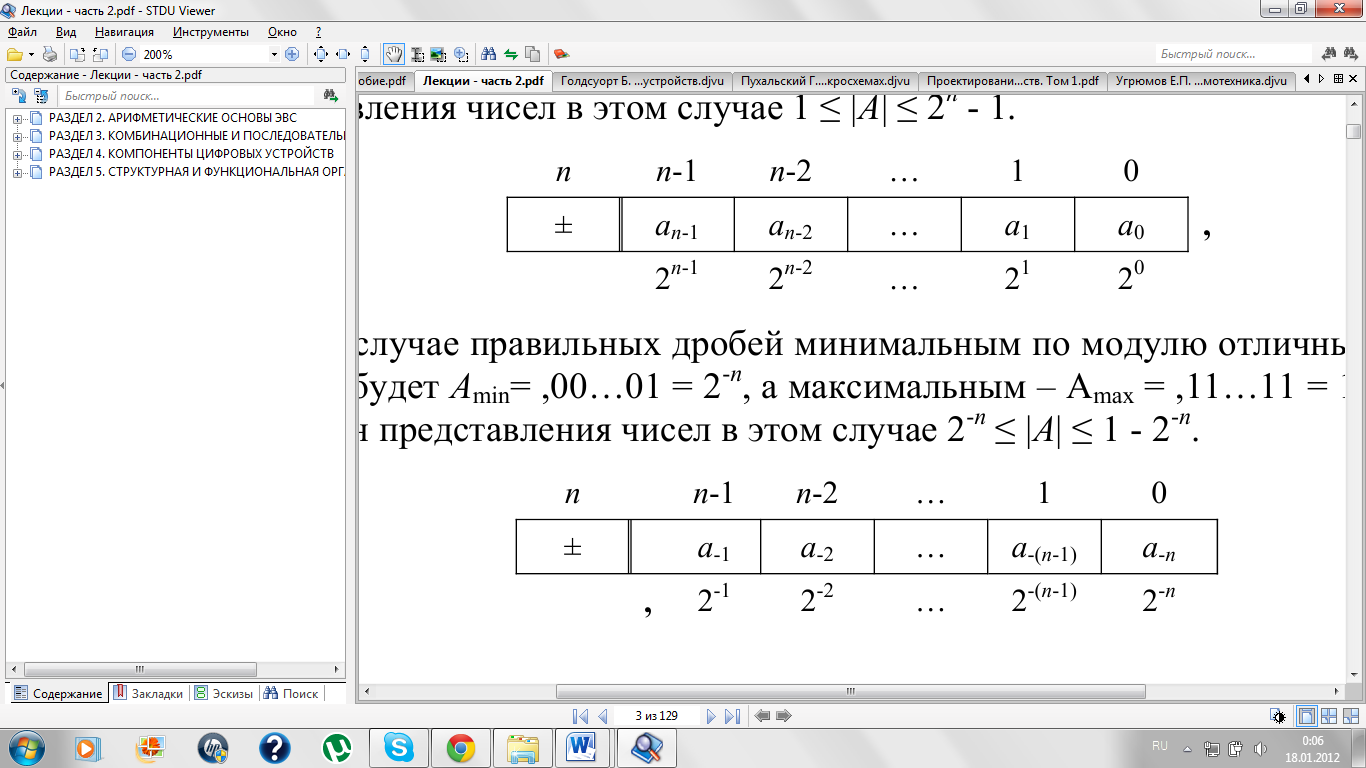
В случае правильных дробей минимальным по модулю отличным от нуля числом будет Аmin= ,00…01 = 2^-n, а максимальным – Аmax = ,11…11 = 1 - 2^-n, т. е. диапазон представления чисел в этом случае 2^-n ≤ |A| ≤ 1 - 2^-n.

Достоинство фиксированной запятой: имеется возможность построить сравнительно несложные арифметические устройства с высоким быстродействием.