20. Счетчики с недвоичным кодированием. (продолжение)

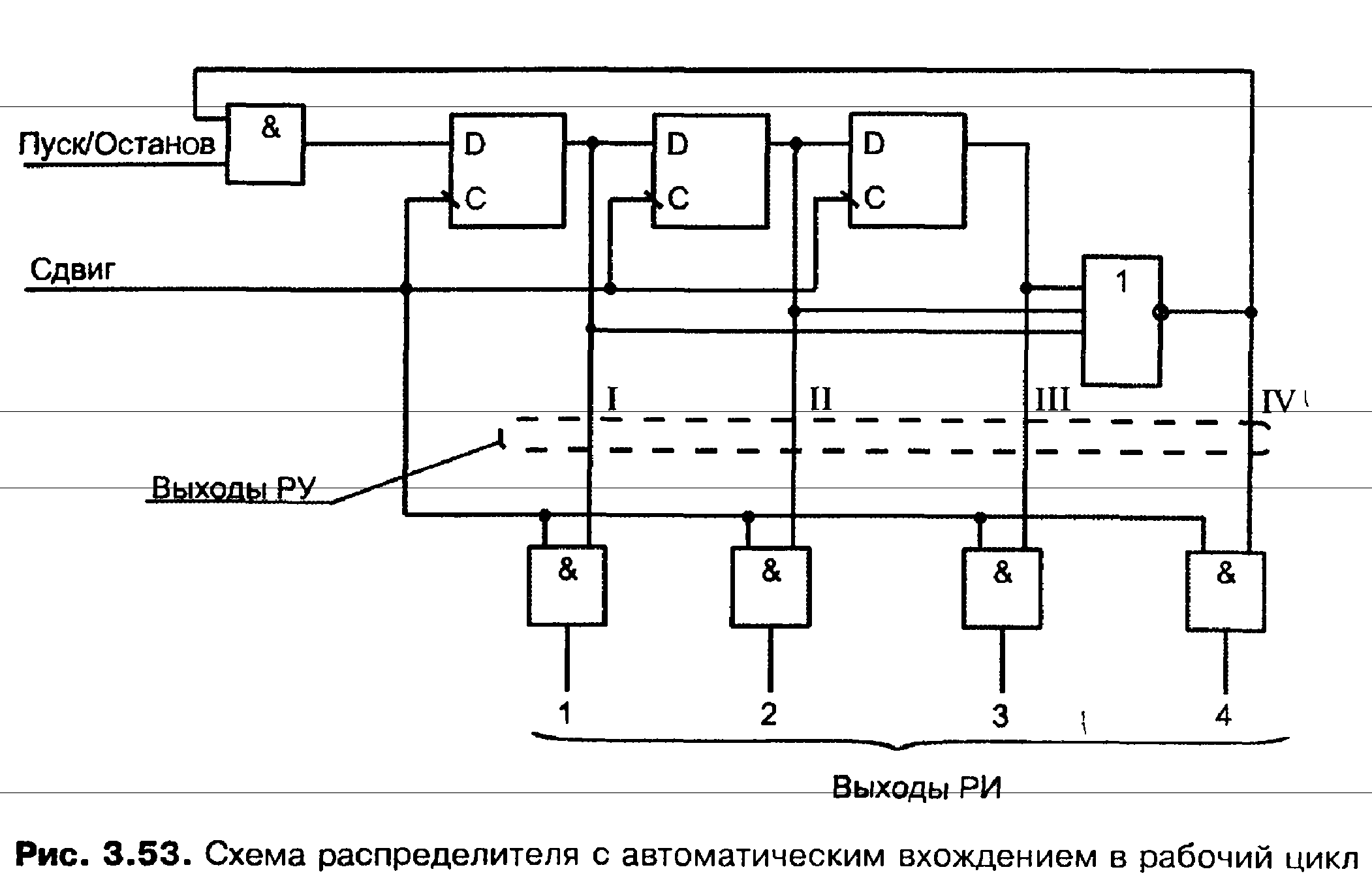
Распределители на кольцевых регистрах находят применение при малом числе выходных каналов, когда необходимость иметь по триггеру на каждый канал не ведет к чрезмерно большим аппаратурным затратам. Достоинством распределителей на кольцевых регистрах является отсутствие дешифраторов в их структуре и, как следствие, высокое быстродействие (задержка перехода в новое состояние равна времени переключения триггера).

Кольцевой регистр с перекрестной обратной связью (счетчик Джонсона, счет­чик Мебиуса, счетчик Либау-Крейга) имеет обратную связь на первый триггер от инверсии выходного сигнала . Он имеет 2n состоя­ний, т. е. при той же разрядности вдвое больше, чем обычный кольцевой регистр. В то же время выход счетчика Джонсона представлен не в коде "1 из N", что требует преобразования кодов для получения выходов распре­делителя тактов. Такие преобразователи очень просты, что обуславливает применение счетчиков Джонсона в составе распределителей.

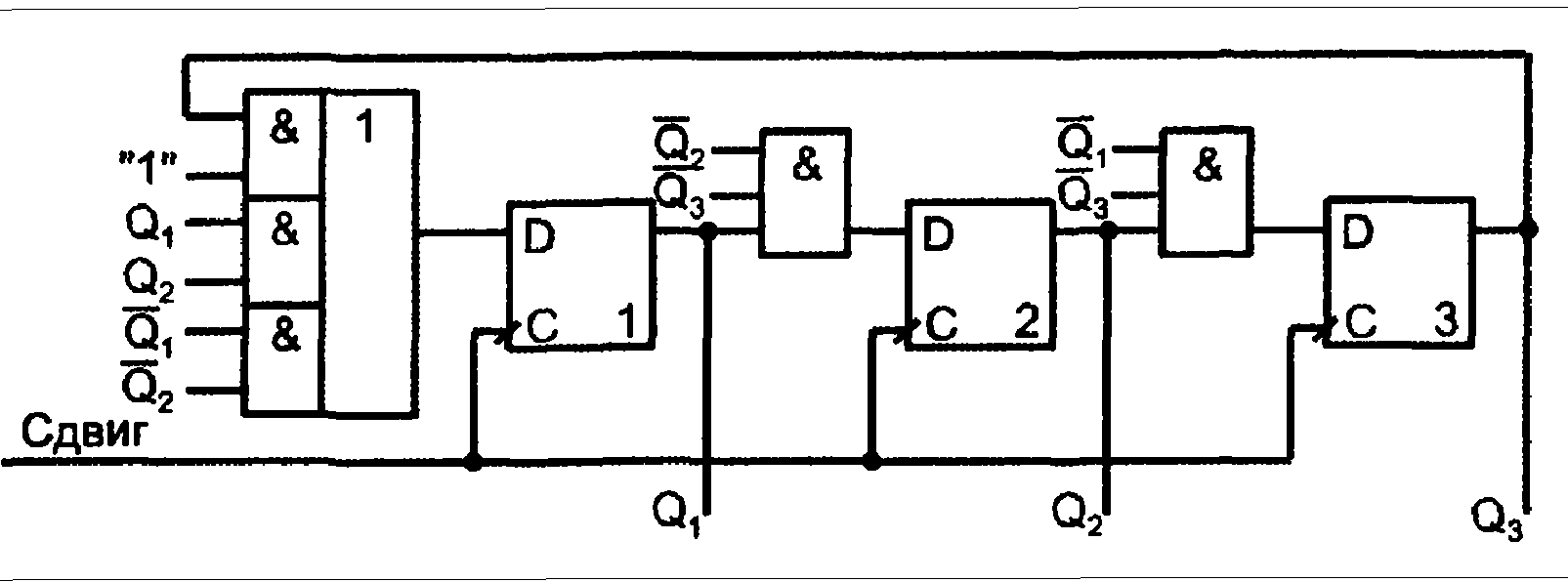
Особенность рассмотренной схемы — четное число состояний при любом n (2n — всегда число четное). Обычный кольцевой регистр такого ограниче­ния не имеет.

Преобразование выходного кода счетчика Джонсона в код "1 из N" требует добавления всего опного лвухвхопового элемента И либо И-HЕ для кяждогд выхода распределителя тактов. Принцип дешифрации состоит в выявлении положения характерной координаты временной диаграммы — границы меж­ду зонами единиц и нулей.

21. Полиномиальные счетчики.

Полиномиальные счётчики строятся на основе n-разрядного регистра сдвига с линейными обратными связями (с сумматорами по модулю два в цепи обратной связи).

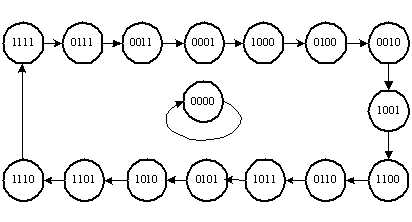
В качестве примера рассмотрим схему счётчика при n = 4 :

П оследовательность состояний регистра сдвига представлена на рис. 10.4 (состояние 0 0 0 0 запрещено).

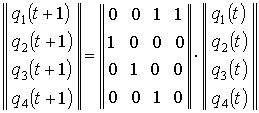
Работа схемы описывается с помощью квадратной матрицы С, связывающей данное   и последующее  состояния. Для нее состояния триггеров q₁, q₂, q₃ и q₄ в момент времени (t + 1) определятся следующим образом:

или в матричной форме или где

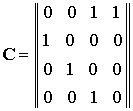
Первая строка в матрице C определяется видом обратной связи регистра сдвига, остальные единичные элементы матрицы определяют операцию сдвига содержимого регистра.

Периодические свойства последовательностей на выходах счетчика определяются характеристическим многочленом  , который является определителем матрицы   (Е – единичная матрица).

Если многочлен   неприводим и примитивен, то счетчик будет формировать последовательность максимальной длины или М- последовательность. Для данного примера характеристический многочлен j (х) неприводим, примитивен и имеет следующий вид:   = x4   x   1.

Вероятности появления символа 1   и символа 0  для М-последовательности определяются следующим образом: ,  .

И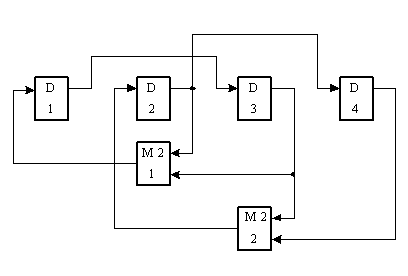 звестен оригинальный метод построения счетчика на регистре с s-шаговым сдвигом за один рабочий такт ( ). Запишем следующие соотношения:   ,  и т.д.

Пусть s = 2. Тогда матрица   будет имеет вид:

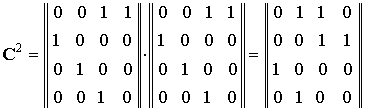
По матрице   построим схему счетчика: ->

П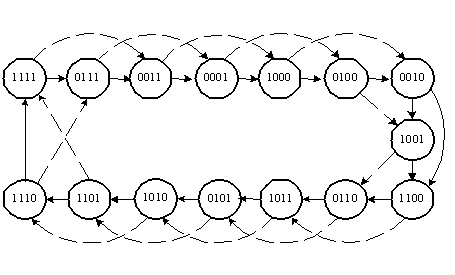 оследовательность состояний регистра сдвига при s = 2 (пунктирные линии) и при s = 1 (сплошные линии) показаны на рис. 10.6:

К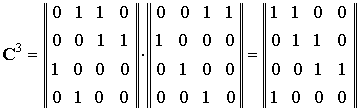 ак видно из рисунка, счетчик также формирует М-последовательность. Возьмем s = 3. Матрица функционирования счетчика в этом случае имеет вид: