41. Доказательство критерия седловой точки матрицы игры размерности в терминах пассивных стратегий.

Для того чтобы в игре с матрицей А раз­мера 2x2 существовала седловая точка необходимо и доста­точно, чтобы одна из чистых стратегий являлась пассивной.

Доказательство.

Необходимость. Пусть i, k {1, 2}, i k, – номера чистых стратегий игрока А, а j, l {1, 2},j l, – номера чистых стратегий игрока В. Пусть – седловая точка. Тогда A_i – оптимальная стратегия игрока А.

Так как чистую оп­тимальную стратегию A_i можно рассматривать как смешанную оптимальную стратегию, в которую чистая стратегия A_i входит достоверно, т. е. с вероятностью, равной 1, а чистая стратегия A_k – c нулевой вероятностью, то стратегия А_k является пассивной, и необходимость доказана.

Отметим, что из того, что – седловая точка, аналогичным образом следует, что B_l — пассивная стратегия игрока В.

Достаточность. Пусть одна из чистых стратегий, напри­мер, стратегия А_k игрока А является пассивной. Тогда найдется оптимальная смешанная стратегия Р⁰ игрока А, в которую чистая стратегия А_k входит с нулевой вероятностью и, следовательно, чистая стратегия А_k входит с вероятностью, равной единице. Это означает, что Р⁰ = A_i, т. е. A_i – оптимальная стратегия.

Пусть Q⁰ – некоторая оптимальная стратегия игрока В, в кото­рую чистые стратегии В_j и В_l входят соответственно с вероятностями q⁰ и 1 – q⁰ . Так как q⁰+(1 – q⁰)= 1, то хотя бы одно из чисел q⁰ и 1 – q⁰ положительно.

Если q⁰ = 1 и, следовательно, 1 – q⁰ = 0, то чистая стратегия В_j является активной и тогда, по теореме об активных страте­гиях

(1)

где V- цена игры.

В то же время стратегия B_j является оптималь­ной, так как в случае q⁰ = 1, имеет место равенство B_j = Q⁰, a Q⁰ – оптимальная стратегия. Из равенства с учетом оптималь­ности стратегий А_i и B_j следует, что – седловая точка.

Если q⁰ = 0 и, следовательно, 1 – q⁰ = 1, то чистая стратегия В_j является активной оптимальной стратегией и тогда из равенства

(2)

которое имеет место в силу теоремы об активных стратеги­ях, следует, что — седловая точка.

Наконец, рассмотрим случай q⁰ > 0 и 1 – q⁰ > 0. В этом случае стратегии B_j и B_l активны и тогда по теореме об активных стратегиях имеют место оба равенства .

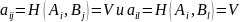Могут представиться две возможности:

(3)

и

(4)

1. Рассмотрим возможность .

В силу (1) и (2) для показателя эффективности стратегии А_i будем иметь

Из неравенства (3) и равенства (1) следует, что

Из (5) и (6) получаем двойное равенство

которое означает, что A_i и B_j - оптимальные стратегии. Следовательно, – седловая точка матрицы А.

2. Рассмотрим возможность .

Если , то это нера­венство вместе с неравенством будет означать, что i-я строка матрицы А строго доминируется k-й строкой и потому i-ю строчку нужно отбросить как заведомо не выгодную, что противоречит оптимальности стратегии А_i. Значит, . Но так как по (2) и (1) , то элемент наименьший в i-й строке (на самом деле равный ) и наибольший в l-м столбце, т. е. — седловая точка матрицы А.