5.5Электронный микроскоп, понятие об электронной оптике.

ЭЛЕКТРОННАЯ И ИОННАЯ ОПТИКА занимается вопросами формирования, фокусировки и отклонения пучков эл-нов и ионов и получения с их помощью изображений под воздействием электрич. и магн. полей в вакууме. Электронные и ионные изображения можно визуализировать на люминесцентном экране или фотослое. Т. к. электронные пучки используют гораздо шире, чем ионные, весьма распространён термин «электронная оптика» (ЭО).

В основе работы электронного микроскопа лежит свойство неоднородных электрических и магнитных полей, обладающих вращательной симметрией, оказывать на электронные пучки фокусирующее действие. Таким образом, роль линз в электронном микроскопе играет совокупность соответствующим образом рассчитанных электрических и магнитных полей; соответствующие устройства, создающие эти поля, называют «электронными линзами».

В зависимости от вида электронных линз электронные микроскопы делятся на магнитные, электростатические и комбинированные.

Так же как и в случае оптического микроскопа объекты, во-первых, могут быть «самосветящимися», т. е. служить источником электронов. Это, например, накаленный катод или освещаемый фотоэлектронный катод. Во-вторых, могут быть использованы объекты, «прозрачные» для электронов, обладающих определённой скоростью. Иными словами, при работе на просвет объекты должны быть достаточно тонкими, а электроны достаточно быстрыми, чтобы они проходили сквозь объекты и поступали в систему электронных линз. Кроме того, путём использования отражённых электронных лучей могут быть изучены поверхности массивных объектов (в основном металлов и металлизированных образцов). Такой способ наблюдения аналогичен методам отражательной оптической микроскопии.

По характеру исследования объектов электронные микроскопы разделяют на просвечивающие, отражательные, эмиссионные, растровые, теневые и зеркальные.

Наиболее распространёнными в настоящее время являются электромагнитные микроскопы просвечивающего типа, в которых изображение создаётся электронами, проходящими сквозь объект наблюдения. Он состоит из следующих основных узлов: осветительной системы, камеры объекта, фокусирующей системы и блока регистрации конечного изображения, состоящего из фотокамеры и флуоресцирующего экрана. Все эти узлы соединены друг с другом, образуя так называемую колонну микроскопа, внутри которой поддерживается давление. Осветительная система обычно состоит из трёхэлектродной электронной пушки (катод, фокусирующий электрод, анод) и конденсорной линзы (речь идёт об электронных линзах). Она формирует пучок быстрых электронов нужного сечения и интенсивности и направляет его на исследуемый объект, находящийся в камере объектов. Пучок электронов, прошедший сквозь объект, поступает в фокусирующую (проекционную) систему, состоящую из объективной линзы и одной или нескольких проекционных линз.

6 Тема

6.1Основы квантовой механики.

Квантовая механика - раздел теоретической физики, описывающий физические явления, в которых действие сравнимо по величине с постоянной Планка. Предсказания квантовой механики могут существенно отличаться от предсказаний классической механики. Поскольку постоянная Планка является чрезвычайно малой величиной по сравнению с действием повседневных объектов, квантовые эффекты в основном проявляются только в микроскопических масштабах. Если физическое действие системы намного больше постоянной Планка, квантовая механика органически переходит в классическую механику. В свою очередь, квантовая механика является нерелятивистским приближением (то есть приближением малых энергий по сравнению с энергией покоя массивных частиц системы) квантовой теории поля.

Классическая механика, хорошо описывающая системы макроскопических масштабов, не способна описать явления на уровне молекул, атомов, электронов и фотонов. Квантовая механика адекватно описывает основные свойства и поведение атомов, ионов, молекул, конденсированных сред, и других систем с электронно-ядерным строением. Квантовая механика также способна описывать поведение электронов, фотонов, а также других элементарных частиц, однако более точное релятивистски инвариантное описание превращений элементарных частиц строится в рамках квантовой теории поля. Эксперименты подтверждают результаты, полученные с помощью квантовой механики.

Основными понятиями квантовой кинематики являются понятия наблюдаемой (является линейным самосопряжённым оператором, действующим на сепарабельном (комплексном) гильбертовом пространстве чистых состояний квантовой системы) и состояния (любое возможное состояние, в котором может находиться квантовая система).

Математический аппарат нерелятивистской квантовой механики строится на следующих положениях:

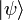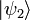1. Чистые состояния системы описываются ненулевыми векторами комплексного сепарабельного гильбертова пространства H причем векторы и описывают одно и то же состояние тогда и только тогда, когда 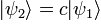где с — произвольное комплексное число.

2. Каждой наблюдаемой можно однозначно сопоставить линейный самосопряжённый оператор. При измерении наблюдаемой 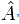, при чистом состоянии системы 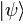в среднем получается значение, равное 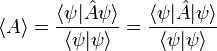где через 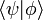обозначается скалярное произведение векторов и .

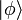3. Эволюция чистого состояния гамильтоновой системы определяется уравнением Шрёдингера 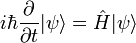где — гамильтониан.

Основные следствия этих положений:

- При измерении любой квантовой наблюдаемой, возможно получение только ряда фиксированных её значений, равных собственным значениям её оператора — наблюдаемой.

- Наблюдаемые одновременно измеримы (не влияют на результаты измерений друг друга) тогда и только тогда, когда соответствующие им самосопряжённые операторы перестановочны.

Эти положения позволяют создать математический аппарат, пригодный для описания широкого спектра задач в квантовой механике гамильтоновых систем, находящихся в чистых состояниях. Не все состояния квантовомеханических систем, однако, являются чистыми. В общем случае состояние системы является смешанным и описывается матрицей плотности, для которой справедливо обобщение уравнения Шрёдингера — уравнение фон Неймана (для гамильтоновых систем). Дальнейшее обобщение квантовой механики на динамику открытых, негамильтоновых и диссипативных квантовых систем приводит к уравнению Линдблада.