2. Силовое исследование механизма

2.1 Определение сил, действующих на звенья механизма

Используя план ускорений для положения механизма, соответствующего угловой координате кривошипа φ₁=90^о, определим ускорения центров тяжести звеньев:

a_S1 = (P_aS₁)·μ_a = 47,15 · 0,05 = 2,357 м/с²

a₂ = (P_aS₂)·μ_a = 77,1 · 0,05 = 3,855 м/с²

a_S3 = (P_aS₃)·μ_a = 51,97 · 0,05 = 2,599 м/с²

Определим массы звеньев по формуле:

,

где – масса i-го звена; – длина i-го звена; q=80 кг/м – масса одного метра звена.

m₁ = q · l_OA = 80 · 0,105 = 8,4 кг

m₂ = q · l_AB = 80 · 0,285 = 22,8 кг

m₃ = q˖l_CD = 80 · 0.285 = 22,8 кг

Определим центральные моменты инерции звеньев 2 и 3 по формуле:

,

где – центральный момент инерции i-го звена; – масса i-го звена; – длина

i-го звена.

J_S2 = (m₂ · l₂² )/12= (22,8 · 0,285)/12 = 0,154 кг·м²

J_S3 = (m₃ · l₃² )/12= (22,8 · 0,285)/12 = 0,154 кг·м²

Определим силы тяжести звеньев 1,2 и 3 по формуле :

G₁ = m₁ ˖ g = 8,4 ˖ 9,81 = 82,376 Н

G₂ = m₂ ˖ g = 22,8 ˖ 9,81 = 223,591 Н

G₃ = m₃ ˖ g = 22,8 ˖ 9,81 = 223,591 Н

Определение сил инерции звеньев 2 и 3 по формуле :

Fu₂ = m₂ · aS₂ = 22,8 · 3,855 = 87,894 Н

Fu₃ = m₃ · aS₃ = 22,8 · 2,599 = 59,246 Н

Определяем моменты сил инерции звеньев 2 и 3 по формуле :

Mu₂ = JS₂ · ε₂ = 0,154 · 6,196 = 0,956 Н·м

Mu₃ = JS₃ · ε₃ = 0,154 · 2,524 = 0,389 Н·м

Момент сил заменяем парами сил:

Они направлены противоположно угловым ускорениям звеньев.

2. Определение усилий в кинематических парах и уравновешивающего момента методом Бруевича

Розглянемо пари елементів окремо і визначимо реакції в парах елементів. Для цього викреслюємо кінематичні групи:

.

Прикладаємо сили тяжіння ланок, сили інерції. Дію відкинутих зв’язків (ланок) механізму замінюємо силами реакцій.

Структурна група 2-3.

На неї діє сили тяжіння G₂ та G₃, сили інерції та , реакції , та , пари сил Р_u2= Р^’_u2 та Р_u3= Р^’_u3 та сила опору обертанню коромисла Pс=10·G₃.

Складаємо рівняння рівноваги групи відносно точки B.

звідки

звідки

Будуємо силовий многокутник :

Із креслення знаходимо:

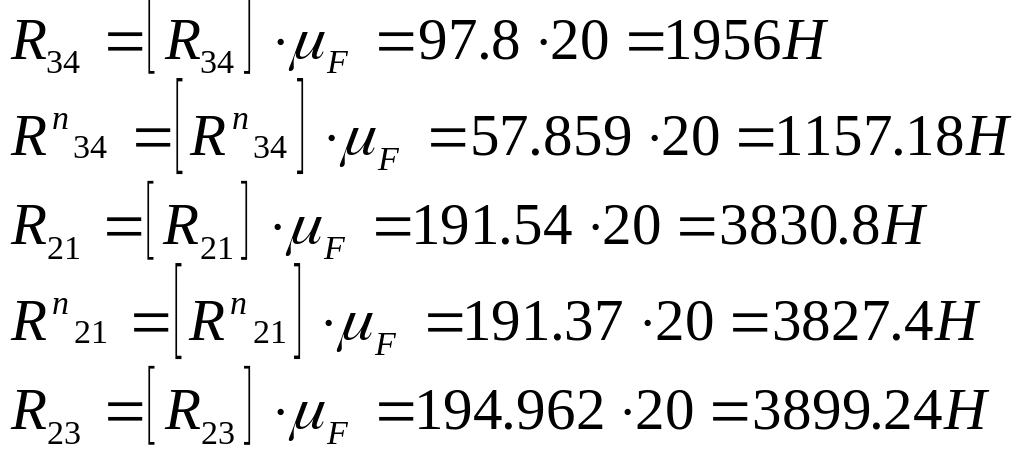
Структурна група 1 - 4 (кривошип зі стійкою)

На кривошип діють зусилля: реакції та , врівноважуюча сила .

Визначаємо величину врівноважуючого моменту :

;

2. Определение уравновешивающего момента способом

Н.Е. Жуковского

Строим повернутый на 90˚ план скоростей в масштабе μV =0,05 (м/с)/мм. На этот план переносим все активные силы. При этом Му заменяем парой сил Ру и Ру΄.

Составляем уравнение равновесия для определения силы Ру:

F_y*P_Va-P_u2*ab+P_u3*P_Vb-P_c*P_Vd+F_u2*h₇+F_u3*h₈+G₁*_h9+G₂*h₁₀+G₃*h₁₁=0

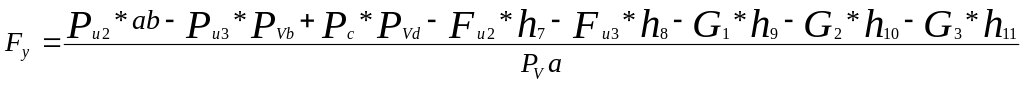
Уравновешивающий момент по способу Жуковского будет равен:

M_у^Ж = F_у · l_OA= 3868.3 · 0,105 = 406.17 Н·м

Погрешность Му определяем по формуле:

Δ = |M_у - M_у^Ж|/ M_у^Ж = 0.002%

Погрешность меньше 5% - значит задача, решена правильно.

3.Синтез зубчатой передачи

3.1 Расчет параметров зацепления

Исходные данные к расчету:

Числа зубьев зубчатых колес Z₄ = 14, Z₅ = 32.

Модуль всех зубчатых колес m = 4

Коэффициент высоты головки зуба h_a^* = 1

Коэффициент радиального зазора c^* = 0,25

Угол профиля исходного контура α = 20˚

Параметры, которые не изменяются в результате смещения:

- шаг по делительной окружности

p = πm = 3,1416 · 4 = 12,566 мм

- радиусы делительной окружности

r₁ = 0,5mZ₄ = 0,5 · 4 · 14 = 28 мм

r₂ = 0,5mZ₅ = 0,5 · 4 · 32 = 64 мм

- радиусы основных окружностей

r_b1 = r₁ · cosα = 28 · 0,93969 = 26.311 мм

r_b2 = r₂ · cosα = 64 · 0,93969 = 60.140 мм

- шаг по основной окружности

Pb = p · cosα = 12.566 · 0,93969 = 11.809мм

Параметры неравномерного зацепления:

Коэффициенты смещения X₁ = 0,540; X₂ = 0,441;

Угол зацепления

Применив метод интерполяции, получим

;

- радиусы начальных окружностей

r_w1 = 0,5mZ₁ = 0,5 · 4 · 14 · = 29.059 мм;

r_w2 = 0,5mZ₂ = 0,5 · 4 · 32 · = 66.421 мм;

- межосевое расстояние

a_w = r_w1 + r_w2 = 29,059 + 66,421= 95,48 мм;

- радиусы окружностей впадин

;

r_f1 = m (0,5Z₁ - h_a^* - c^* + X₁) =4 (0,5 · 14 – 1 – 0,25 + 0,540) = 25,16 мм;

r_f2 = m (0,5Z₂ - h_a^* - c^* + X₂) = 4 (0,5 · 32 – 1 – 0,25 + 0,441) = 60,764 мм;

- высота зуба

h = a_w - r_f1 - r_f2 - с^* ∙ m = 95,48 – 25,16– 60,764 – 0,25 · 4 = 8,556 мм;

- радиусы окружностей вершин

r_a1 = r_f1 + h = 25,16 + 8,556 = 33,716 мм;

r_a2 = r_f2 + h = 60,764 + 8,556 = 69,32 мм;

- толщина зубьев по делительным окружностям

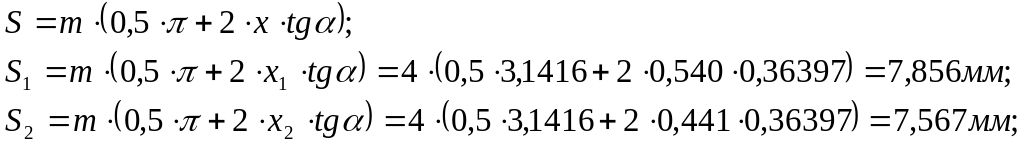
- толщины зубьев по основной окружности

;

S_b1 = 2 r_b1 ( + invα) = 2 · 26,311 () = 8,166 мм;

S_b2 = 2 r_b2 ( + invα) = 2 · 60,140 () = 8,904 мм;

- толщины зубьев по начальным окружностям

;

S_w1 = 2 r_w1 ( + invα - invα_w) = 2 · 29,059 (+ 0,035-0,0459 ) = 7,25 мм;

S_w2 = 2 r_w2 ( + invα - invα_w) = 2 · 66,421() = 5,791 мм;

- шаг начальной окружности

- углы профиля на окружностях вершин αα определяются по формуле:

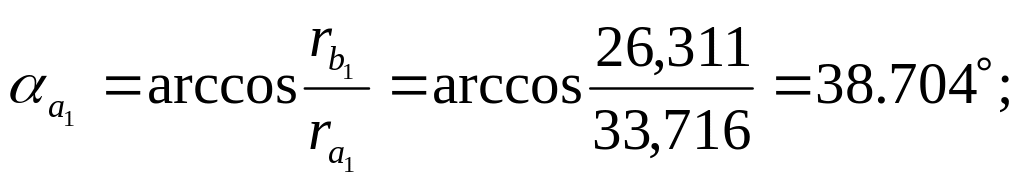
- толщины зубьев по окружности вершин

S_a1 = 2 r_a1 ( + invα – invα_a1) = 2 · 33,716 (+ 0,035-0,125751) = 1,985 мм

S_a2 = 2 r_a2 ( + invα – invα_a2) = 2 · 69,32 () = 2,953 мм;

Коэффициент перекрытия

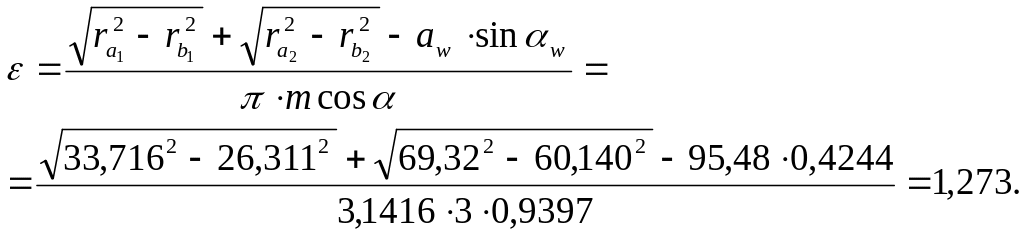
Таблица 7 – Расчетные параметры зацепления

Тип зацепления	z1	z2	m,мм	p,мм	pb	r1	r2	rb1
Нулевое	14	32	4	12,556	11,809	28	64	26,311
Неравносмещенное	14	32	4	12,566	11,809	28	64	26,311
	rb2	x1	x2	aw,град	rw1	rw2	aw,мм	pw
Нулевое	60,140	0	0	20	28	64	92	12,566
еравносмещенное	60,140	0,540	0,441	25,117	29,059	66,421	95,480	13,042
	rf1	rf2	h	ra1	ra2	S1	S2	Sw1
Нулевое	23	59	9	32	68	6,283	6,283	6,283
Неравносмещенное	25,160	60,764	8,566	33,716	69,320	7,856	7,567	7,25
	Sw2	Sb1	Sb2	Sa1	Sa2	E
Нулевое	6,283	6,689	7,697	2,584	2,972	1,565
Неравносмещенное	5,791	8,166	8,904	1,985	2,953	1,273

Проверка качества зубьев и зацепления:

А. Проверка на незаострение Sa≥0,4m

Sa₁≥0,4m Sa₂≥0,4m

1,985≥1,6 2,953≥1,6

Зубья незаострены.

В. Проверка на отсутствие подрезания 0,5Zsin²α≥ – x

0,5Z₁sin²α≥ – x₁ 0,5Z₂sin²α≥ – x₂

0,5·14·sin²20° ≥ 1 – 0,540 0,5·32·sin²20° ≥ 1 – 0,441

0.8188 ≥ 0,46 1,8716 ≥ 0,559

Подрезание отсутствует в обоих случаях.

Результаты расчета приведены в Приложении 1.

Размер по постоянной хорде.

Расположим обкатывающую рейку симметрично полюса станочного зацепления и опустим из полюса перпендикуляры на профиль, чтобы получить точки. В и М касания контура с профилем зуба.

Отрезок, соединяющий эти точки, называется постоянной хордой.

Длина ее обозначается Sc.

S_C1 = S₁·cos²α = 7,856 · 0,93969² = 6,937 мм

S_C2 = S₂·cos²α = 7,567 · 0,93969² = 6,682 мм

Расстояния от окружности вершин до постоянной хорды

h_c1 = r_a1 – r₁ – · sin2α = 33,716 – 28 – · 0,64279 = 4,453 мм

h_c2 = r_a2 – r₂ – · sin2α = 69,32 – 64 – · 0,64279 = 4,104мм

Длина общей нормали.

Длина общей нормали W измеряется скобой. Сначала нужно определить число впадин, охватываемых скобой, из условия, чтобы скоба касалась профилей в эвольвентной их части. Обычно по обе стороны от делительного цилиндра имеется эвольвентный участок профиля, поэтому берут такое число охватываемых зубьев, при котором скоба соприкасается с ними далеко от делительного цилиндра.

При касании скобы с профилями на делительном цилиндре охватываемый ей центральный угол равен 2α. Тогда число шагов, охватываемых скобой (число впадин):

n₁ = = = 1,55

n₂ = = = 3,55

По свойству эвольвенты длина общей нормали равна длине дуги между началами эвольвент на основной окружности. Поэтому при числе n охватываемых впадин длина общей нормали равна:

W₁ = P_bn₁ + S_b1 = 11,809 · 1,55 + 8,166 = 19,975 мм

W₂ = P_bn₂ + S_b2 = 11,809 · 3,55 + 8,904 = 44,329 мм