1.4 Построение планов ускорений и определение угловых скоростей частей механизма

Планы ускорений строим тоже для двух положений: первого заданного и нулевого.

Для положения φ=90^о

Ускорение точки А:

Выбираем отрезок для изображения ускорения точки А:

Тогда масштабный коэффициент ускорений:

Строим план ускорений.

Определим ускорение точки В:

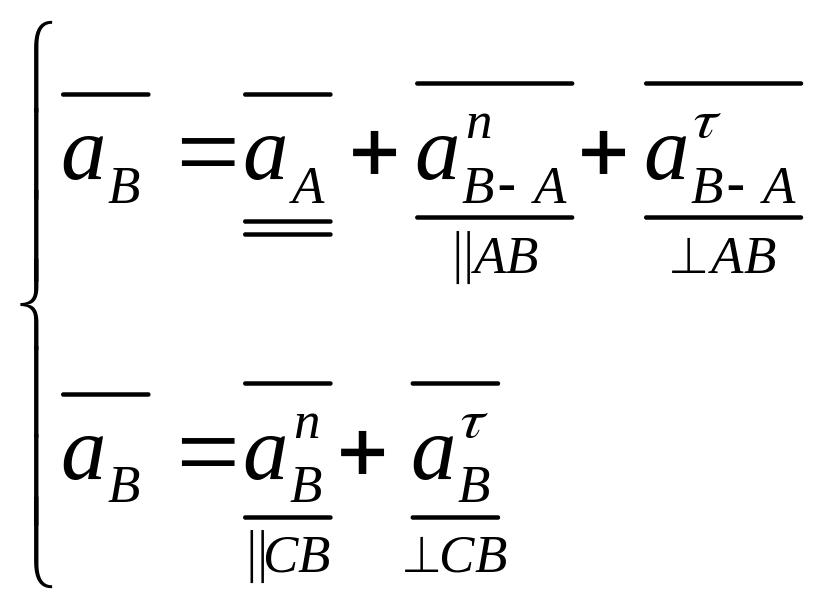
Определим ускорение точки D:

Определяем угловые ускорения звеньев:

Нулевое положение рассчитывается аналогично.

Таблица 3 – Линейные и угловые скорости стержневого механизма

Данные	Положение φ=900	Положение φ0
,	4,716	4,716
,	0,0005	1,738
,	2,98	0
,	1,766	6,217
,	0,416	8,961
,	3,009	8,961
,	1,766	6,456
,	5,198	15,477
,	6,196	21,815
,	2,524	54,307

1.5 Аналитический расчет кинематических параметров движения звеньев механизма

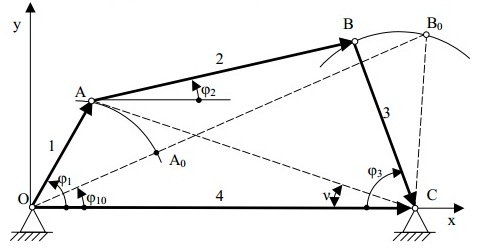
Рисунок 3 - Шарнирный четырехзвенный механизм

Для того чтобы сравнить значения кинематических параметров движения звеньев 2 и 3(рис.3), полученных графическим методом со значениями аналитического метода, в курсовом проекте использованы ЭВМ.

Исходные данные: l_OA = l₁; l_АВ = l₂; l_ВС = l₃; l_ОС = l₄; ω₁ = const.

Угол φ1 – обобщенная координата механизма, определяющая положение кривошипа.

Необходимо определить углы φ₂ и φ₃, определяющие положения шатуна 2 и коромысла 3, угловые скорости этих звеньев ω₂ и ω₃, а также их угловые ускорения ε₂ и ε₃.

Векторный контур, образованный звеньями механизма (рис.3), можно показать уравнением:

.

Спроецировав полученное ранее векторное уравнение на оси x и y, получаем:

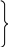
Так как , то , .

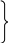В ведем следующие обозначения:

Тогда получаем:

Для удобства введём обозначения:

Тогда, после соответствующих замен, получаем:

Угловые скорости и ускорения звеньев 2 и 3 определяем, взяв первую производную по времени t и выполнив необходимые преобразования:

По приведенному выше алгоритму программа вычисляет значения кинематических параметров движения звеньев 2 и 3, и строит их графики.

Таблица 4 – Данные, вводимые в программу расчета

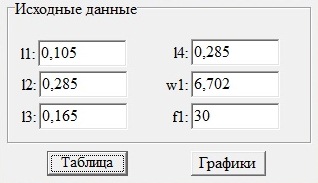
Таблица 5 - Результаты расчета по программе

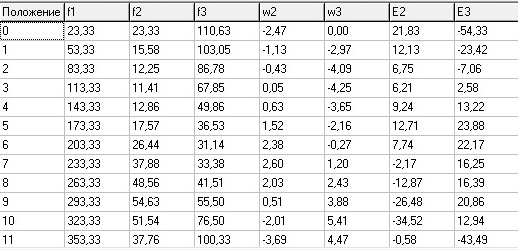
Таблица 6 – Сравнение параметров

Положение механизма	Метод иссле-дования	φ1, град.	φ2, град.	φ3, град.	ω2, рад/с	ω3, рад/с	ε2, рад/с2	ε3, рад/с2
φ1=0о	Аналитич.	23,33	23,33	110,63	-2,47	0,00	21,83	-54,33
	Графич.	23,33	23,33	110,63	2,469	0,00	21,815	54,307
Расхождение в %		0,00	0,00	0,00	0,04	0,00	0,06	0,04
φ1*=90о	Аналитич.	113,33	11,41	67,85	0,05	-4,25	6,21	2,58
	Графич.	113,33	11,41	67,85	0,044	4,25	6,196	2,524
Расхождение в %		0,00	0,00	0,00	1,2	0,00	0,02	2,1

График 1 – Кинематические параметры движения звеньев 2 и 3