Введение

Целью курсового проекта является проектирование и исследование стержневого механизма замыкания контактов, а также зубчатого редуктора.

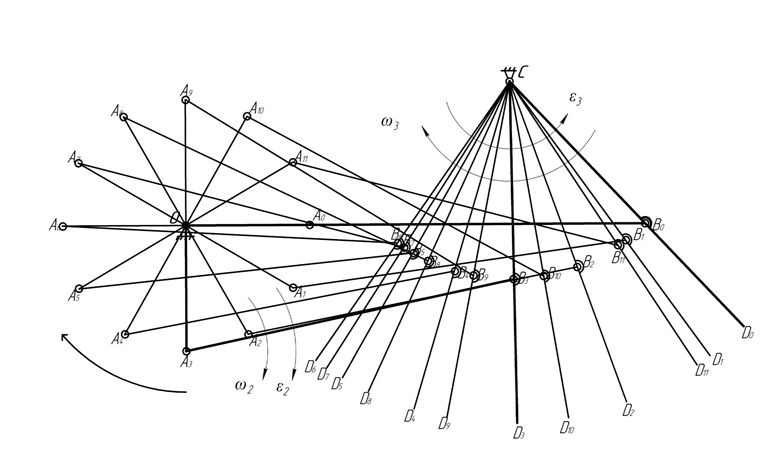
Рисунок 1 – Схема стержневого механизма

Стержневой механизм (рис.1) приводится в движение от электродвигателя через редуктор, состоящий из цилиндрических зубчатых колес 1, 2, 3, 4 и 5(рис.2). Вращательное движение кривошипа АО преобразуется в возвратно-поступательное движение коромысла CBD, которое производит замыкание контактов.

Исходные данные: n_дв=1500мин^-1, n₀=64мин^-1, z₄=14, z₅=32, m=4мм, l_OA=105мм, l_AB=285мм, l_BC=165мм, l_CD=285мм, х=275мм, у=120мм, φ*=90⁰, h=95мм.

Рисунок 2 – Кинематическая схема зубчатого редуктора.

1. Кинематическое исследование механизма

0. 1.1 Структурный анализ механизма

Таблица 1– Характеристика звеньев

№ звена	Название звена	Вид абсолютного движения звена
1	кривошип	вращательное
2	шатун	плоскопараллельное
3	коромысло	возвратно - вращательное
4	стойка	неподвижная

Анализ кинематических пар:

1-4: низшая, плоская (относительное движение вращательное), одноподвижная;

1-2: низшая, плоская (относительное движение вращательное), одноподвижная;

2-3: низшая, плоская (относительное движение вращательное), одноподвижная;

3-4: низшая, плоская (относительное движение вращательное), одноподвижная;

Данная кинематическая цепь замкнутая (т.к. все звенья входят не менее чем в две кинематические пары), плоская (т.к. каждое звено относительно всех остальных звеньев совершает плоское движение) и простая (т.к. все звенья входят в две кинематические пары)

Так как данный механизм плоский для вычисления числа степеней свободы можно использовать формулу Чебышева:

где W – число степеней свободы механизмов,

n – число подвижных звеньев,

P1 – количество одноподвижных пар,

P2 – количество двухподвижных пар.

W=3ˑ(4-1)-2ˑ4-0=1.

4. 1.2 Построение планов механизма

Принимаем μl = 0,002 м/мм и строим 12 положений планов механизма. Длины звеньев на чертеже:

ОА = lOA /μl =0,105/0,002=52,5 мм,

АВ = lAB /μl = 0,285/0,002=142,5 мм,

ВС = lВС /μl=0,165/0,002=82,5 мм,

CD = lCD /μl = 0,285/0,002=142,5 мм.

1.3 Построение планов скоростей и определение угловых скоростей частей механизма

Расчеты скоростей для двух положений механизма.

Определяем ω1:

ω₁ = .

Скорость точки А:

V_А = ω₁ · l_0A =6,7 · 0,105=0,704 м/с.

Определяем масштабный коэффициент: принимаем (Pva) = 70,4 мм, тогда масштабный коэффициент μ_V = 0,01 .

Для положения φ=90^о

Скорость точки B определяем графически:

V_B = V_А + V_B-A , где V_B-A = (ab)·μ_V = 0,13 · 0,01 = 0,013 м/с,

V_B = P_Vb · μV = 70,1 · 0,01 = 0,701 м/с

Скорость точки D определяем по теореме подобия. Составим пропорцию:

P_Vd= = 0,285 · 70,1 / 0,165 = 121,1 м/с,

V_d=P_Vdˑ μ_V=121,1ˑ0,01=1,211 м/с.

Угловые скорости звеньев:

ω₂ = = 0,013 / 0,285 = 0,044 рад/с,

ω₃ = = 0,701/ 0,165 = 4,25 рад/с.

Нулевое положение рассчитывается аналогично.

Таблица 2 – Линейные и угловые скорости стержневого механизма

Данные	Положение φ=900	Положение φ0
VА, м/с	4,716	0,704
VB, м/с	0,0005	0
VB-A, м/с	2,98	0,704
Vd, м/с	1,766	0
ω2, рад/с	0,416	2,469
ω3, рад/с	3,009	0