52. Односторонние функции. Ключевой обмен Диффи-Хеллмана.

Односторонняя (one-way) функция — это функция, которую просто вычислять, но трудно обращать. Пример — умножение больших чисел. Мы можем вычислить без слишком больших трудностей произведение:

но обратный процесс — факторизация (разложение на множители) числа 8 616 460 799 существенно труднее. В.С. Джевонс (W.S. Jevons), рассматривавший эту проблему в 1873 г., резю­мировал, что "мы можем легко... сделать некоторую вещь, но можем иметь много неприятностей, если попытаемся разделить ее".

В качестве операции факторизации для системы с общим ключом нам бы хо­телось иметь такую функцию, которая при работе на сообщении давала бы в результате криптограмму , по которой практически невозможно раскрыть . Другими словами, мы должны быть способны легко выполнять функцию (так, чтобы криптосистема оставалась реализуемой), но реализовать было бы практически невозможно. Заметим, что обращение функ­ции теоретически всегда возможно (скажем, просто путем вычисления для каждого возможного сообщения до тех пор, пока результат не совпадет с ). Однако стоимость выполнения таких вычислений была бы значительно выше, чем значимость информации, которая могла быть получена таким спо­собом, или время, затраченное на это было бы так велико, что полученная информация оказалась бы устаревшей.

Односторонние функции, используемые для криптографических целей, должны обладать еще одним свойством — они должны иметь специальную "лазейку", т.е. способ, с помощью которого некто, обладающий специальным знанием, смог бы восстановить по , затратив разумное количество усилий. Это секретное знание формирует частный ключ, который тайно хранится получателем, позволяя ему расшифровывать сообщения.

Система работает следующим образом.

1. Каждый пользователь имеет пару ключей 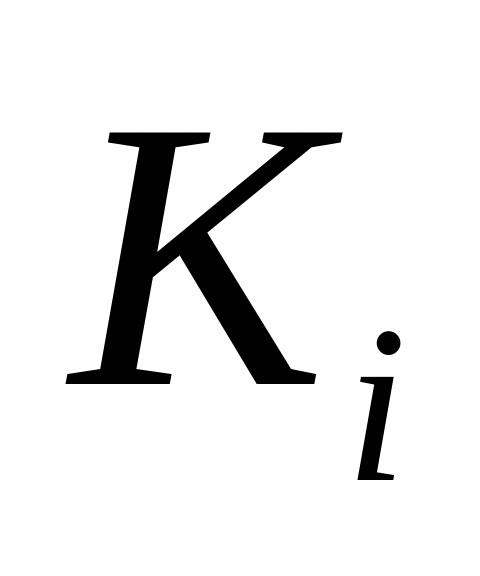и .

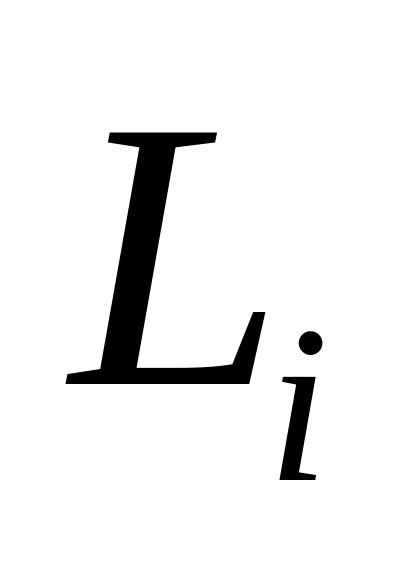2. Сообщение шифруется с помощью функции .

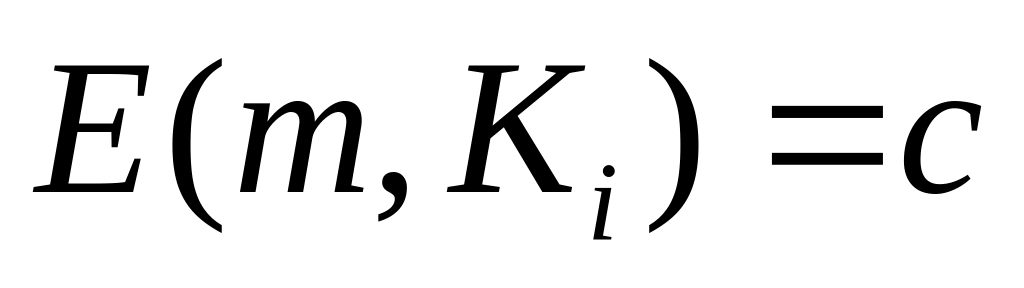3. Выполняется дешифрация с помощью функции .

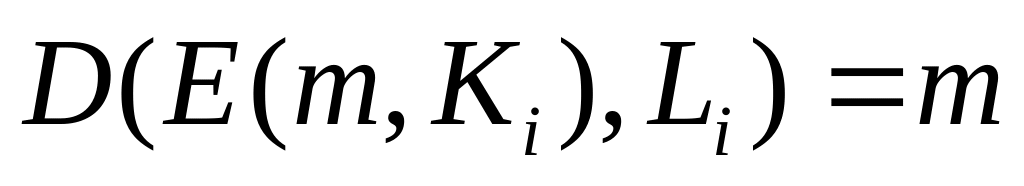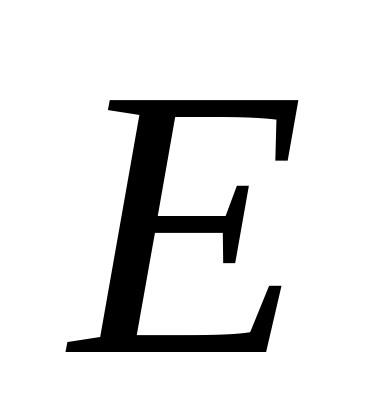4. и 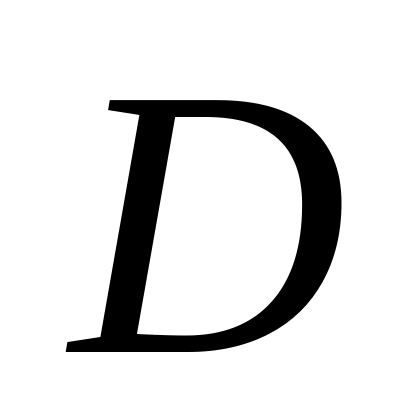проектируются так, чтобы:

   1. для заданных и , можно было легко находить ;

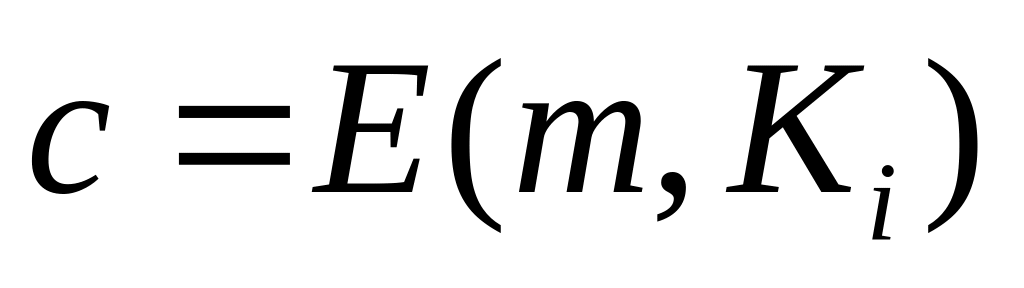   2. для заданного было бы нереально найти (то есть функция должна быть односторонней);

   3. для заданных и , можно было легко найти (то есть функция должна иметь "лазейку", задаваемую параметром ).

Ключевой обмен Диффи-Хеллмана

Протокол обмена ключей Диффи-Хеллмана в действительности не является обычной системой с общим ключом, т.к. передаваемый секрет случаен, но его можно использовать для передачи информации, применяя общий секрет для шифрования передаваемых данных. Это была первая опубликованная система с общим ключом. В ней возникают трудности, связанные с вычисле­ниями логарифмов первичных полей, которые значительно выше, чем при вычислениях с помощью экспоненциальных функций.

Протокол выполняет обмен секретом между двумя сторонами по опасному каналу, не требуя ни знания, ни даже существования этого секрета. Работает это следующим образом.

1. Алиса и Боб соглашаются использовать генератор 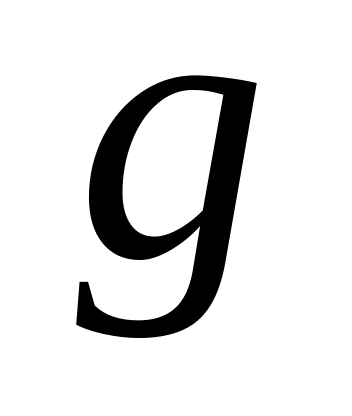и простой модуль .

2. Алиса генерирует случайное число 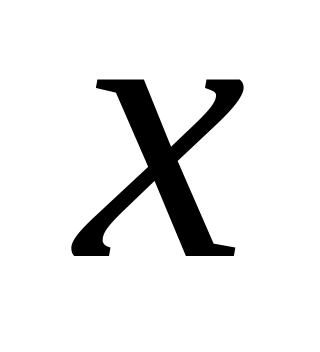. Это ее частный ключ. Она вычисля­ет свой общий ключ 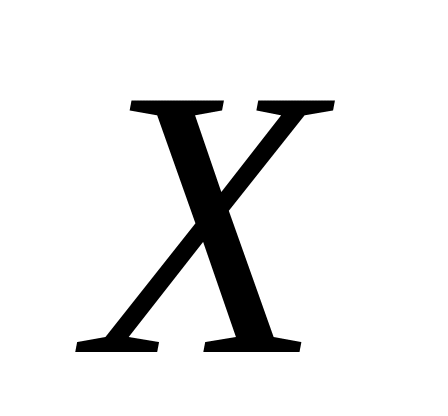, который равен .

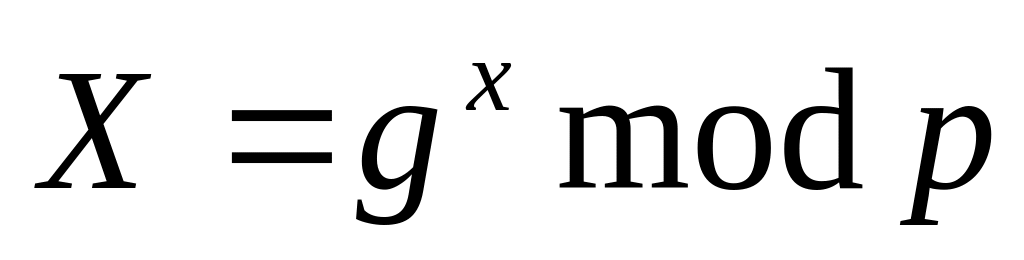3. Подобным же образом Боб генерирует случайный частный ключ 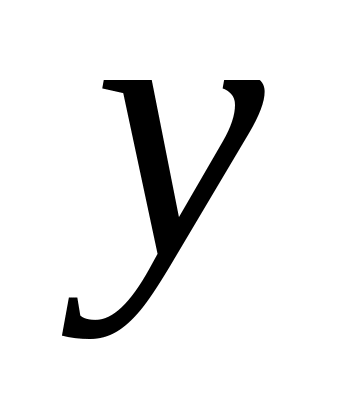и общий ключ 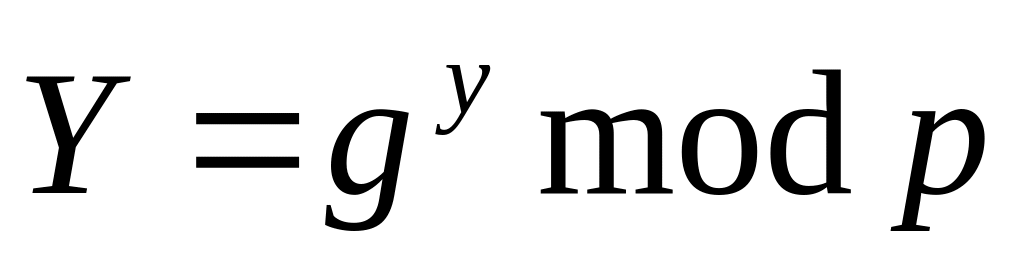. Алиса и Боб обмениваются их общими ключами и .

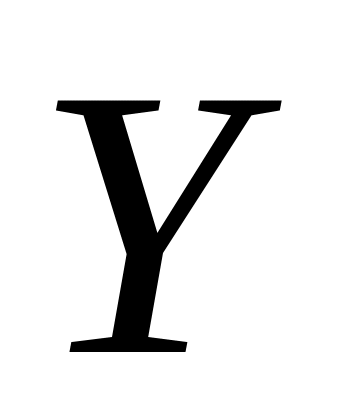4. Алиса принимает ключ и использует свой частный ключ для следую­щего вычисления: .

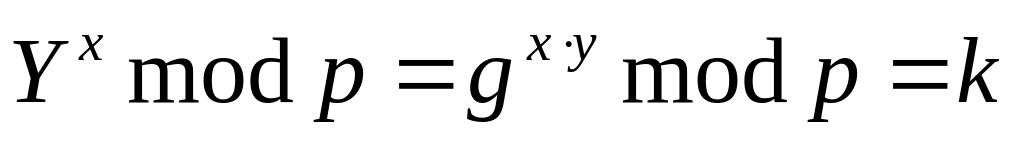5. Боб также может вычислить 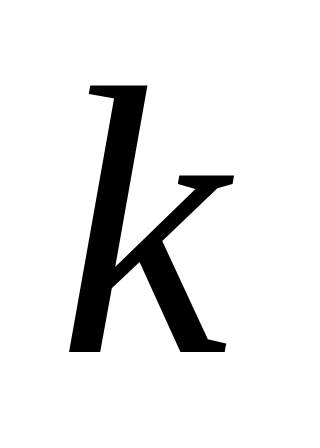по ключу , который он принимает от Али­сы, и своему частному ключу , т.к. .

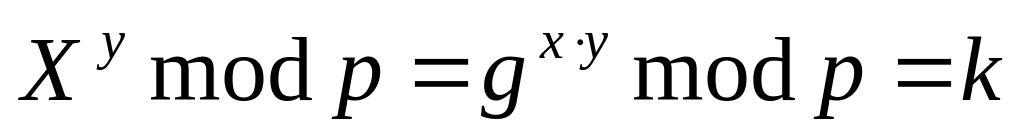6. И Алиса и Боб теперь знают , но подслушивающий не может вычислять по наблюдениям 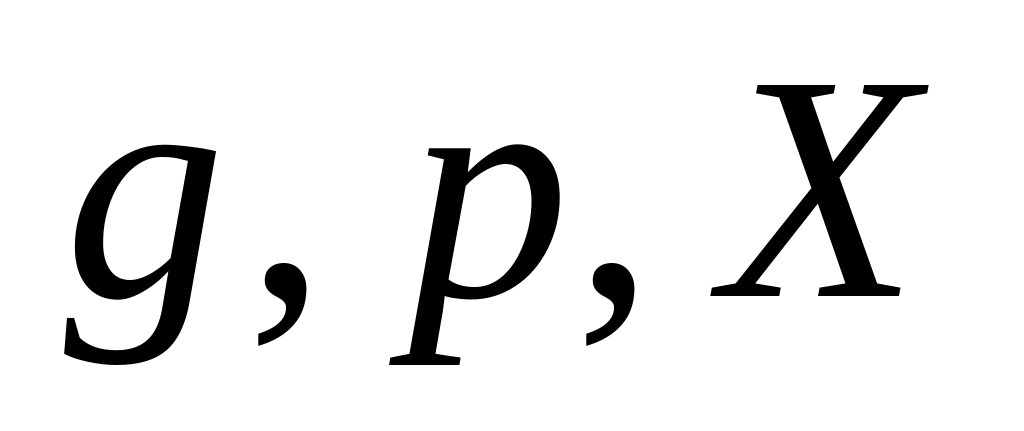и .

В качестве примера такого обмена рассмотрим следующую процедуру:

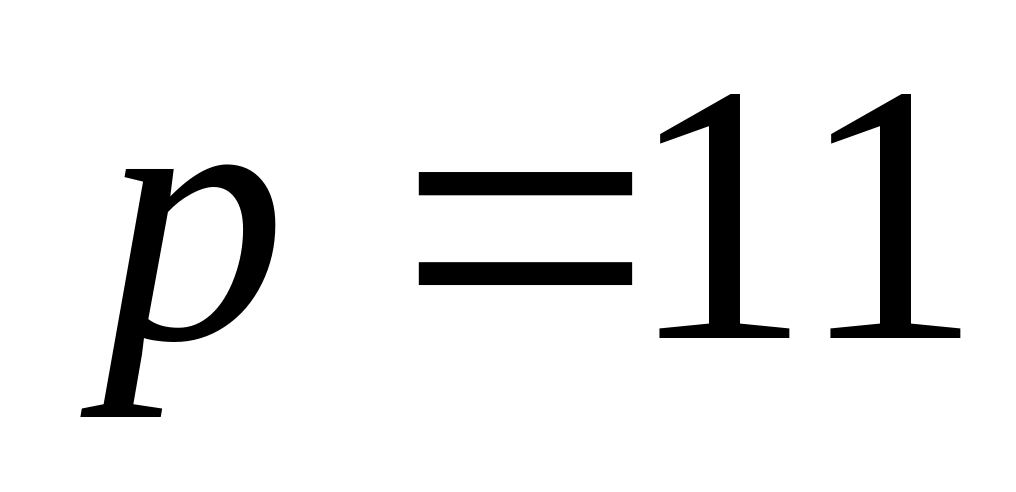1. и .

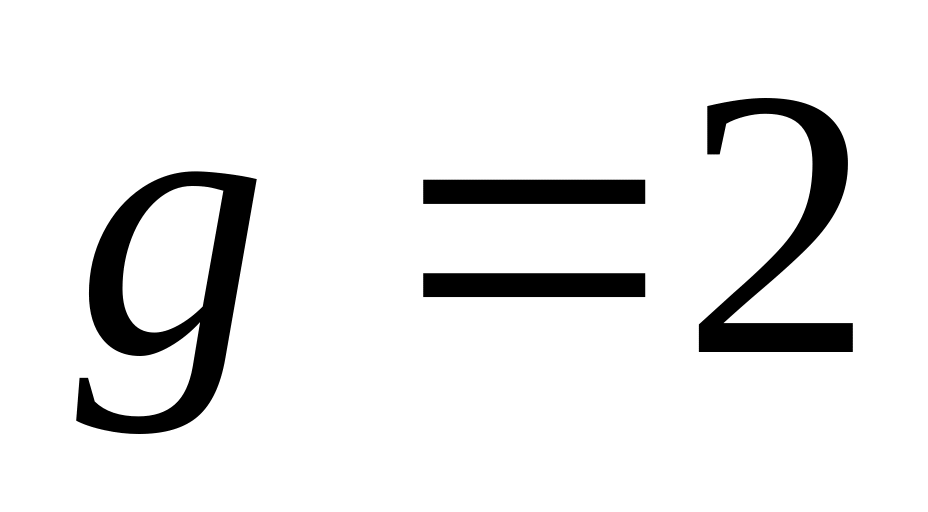2. Алиса получает случайный 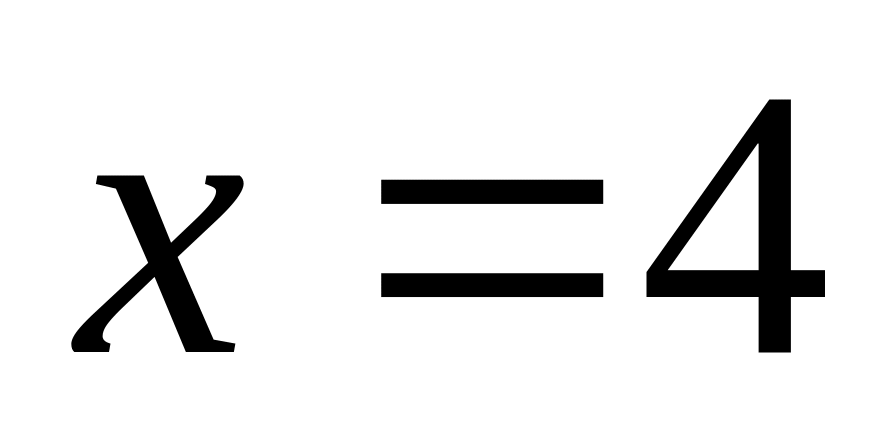, Боб выбирает .

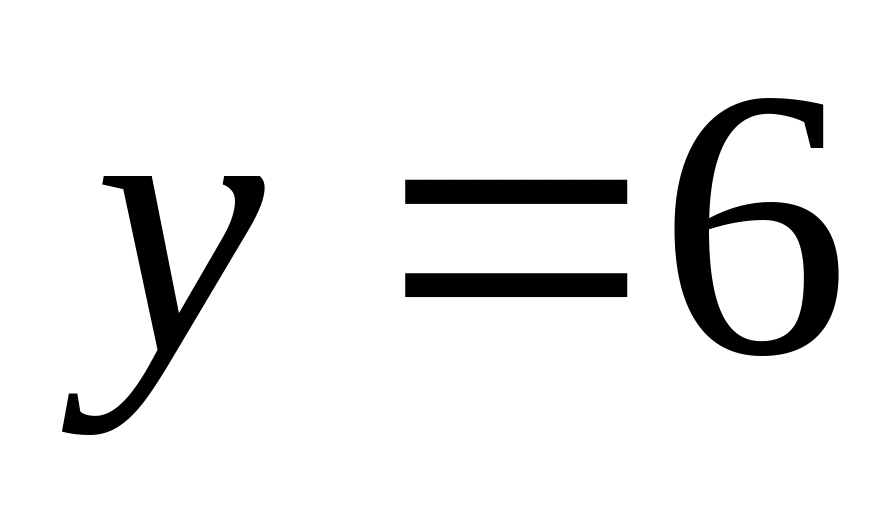3. Алиса вычисляет .

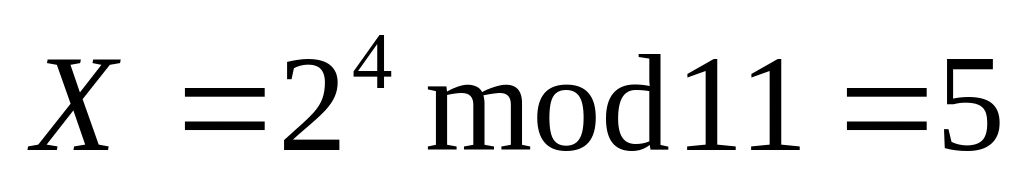4. Боб вычисляет .

5. Алиса посылает Бобу число 5, а Боб посылает Алисе число 9.

6. Алиса вычисляет .

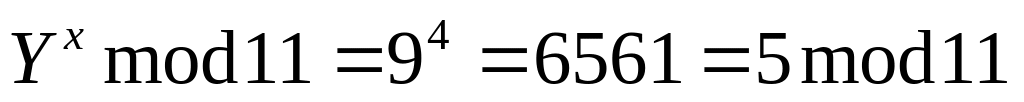7. Боб вычисляет .

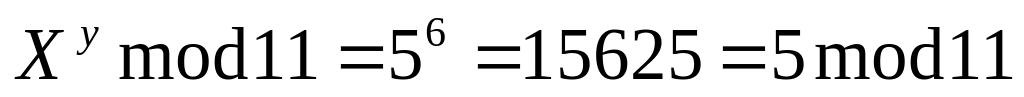8. Поэтому .

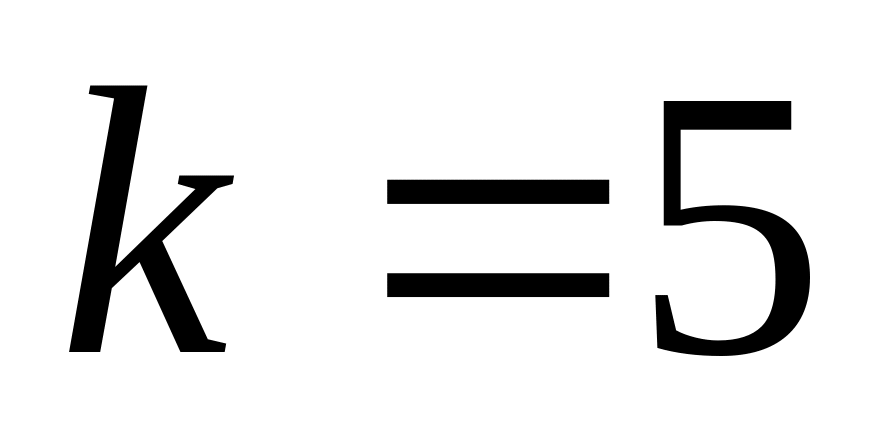Обратите внимание, что общий секрет случаен, т.к. , так что его нельзя использовать, чтобы напрямую посылать информацию. Если Алиса и Боб не выбирают свои частные ключи чисто случайно, то это знание можно использовать для нападения на систему.

Когда и опубликованы, то нападение на эту систему становится эффек­тивным с помощью задачи дискретного логарифмирования. оз­начает, что . Поэтому Ева может находить , вычисляя . В вышеупомянутом примере нахождение триви­ально, но очень трудно, если велико.

33