28. Модель Белла-ЛаПадулы. Основная теорема безопасности Белла-ЛаПадулы.

Данная модель была предложена в 1975 году для формализации механизмов мандатного управления доступом. Мандатный принцип разграничения доступа, в свою очередь, ставил своей целью перенести на АС практику секретного документооборота, принятую в правительственных и военных структурах, когда все документы и допущенные к ним лица ассоциируются с иерархическими уровнями секретности.

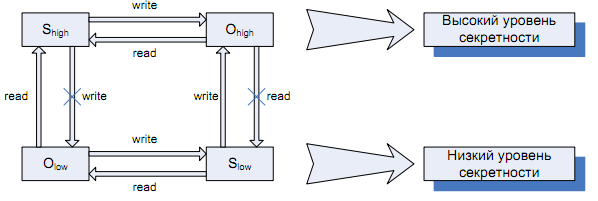
В модели Белла-ЛаПадулы по грифам секретности распределяются S и O, действующие в системе, и при этом выполняются следующие правила:

1. Простое правило безопасности S с уровнем секретности xs может читать информацию из О с уровнем секретности xo тогда и только тогда, когда xs преобладает над xo. No Read Up

2. *-свойство S с уровнем секретности xs может писать информацию в О с уровнем секретности xo в том и только в том случае, когда xo преобладает над xs. No Write Down

Введём следующие обозначения:

- S – множество субъектов; - O – множество объектов, O S ⊂ ; - R={r, w} – множество прав доступа, r – доступ на чтение, w – доступ на запись; - L={U, SU, S, TS} – множество уровней секретности, U- Unclassified, SU – Sensitive but unclassified, S – Secret, TS – Top secret; Λ=( L,<,*, .,?) - решётка уровней секретности; - V – множество состояний системы, представляемое в виде набора упорядоченных пар (F, M), где: F: S ∪ O →L : - функция уровней секретности, ставящая в соответствие каждому S и O в системе определённый уровень секретности; M – матрица текущих прав доступа.

Λ называется алгебраическая система Λ=( L,<,*, .,?) где: - - . - оператор наименьшей верхней границы; - ?- оператор набольшей нижней границы.

Свойства оператора ≤:

1. Рефлексивность: ∀a ∈.L: a<= a’ . С точки зрения уровней безопасности это означает, что разрешена передача информации между S и O одного уровня безопасности.

2. Антисимметричность: ∀a1,a2 ∈.L: a1<= a2 & a2<=a1→a2=a1 . если информация может передаваться как от S и O уровня A к S и O уровня B, так и от S и O уровня B к S и O уровня A, то эти уровни эквивалентны.

3. Транзитивность: : ∀a1,a2,a3 ∈.L: a1<= a2 & a2<=a3→a1<=a3 ∈ ∀ . если информации может передаваться от S и O уровня A к S и O уровня B, и от S и O уровня B к S и O уровня C, то она может передаваться от S и O уровня A к S и O уровня C.

Операторы наименьшей верхней границы a=a1*a2(a1,a2<=a) &(a’∈L: (a’<=a)) →(a’<=a1∨a’<=a2)

Наибольшей нижней границы a=a1?a2( a <= a1,a2) &(a’∈L: (a’<=a1 &a’<=a2)) →(a’<=a)

для каждой пары L a a ∈ 2 , 1 существует единственный элемент наименьшей верхней границы и единственный элемент наибольшей нижней границы.

В качестве уровней безопасности совершенно не обязательно выбирать целые числа, в ряде случаев удобнее использовать более сложные структуры. За счёт этого, например, в пределах каждого уровня секретности можно реализовать категории секретности. В этом случае наличие допуска к той или иной категории информации может служить дополнительным механизмом безопасности, ограничивающим доступ к защищаемым S или O.

Система Σ =(V0,R,T) состоит из следующих элементов:

- v0 – начальное состояние системы; - R – множество прав доступа; -T:V×R →V - функция перехода, которая в ходе выполнения запросов переводит систему из одного состояния в другое.

Изменение состояний системы во времени происходит следующим образом: система, находящаяся в состоянии v ∈V, получает запрос на доступ R r ∈ и переходит в состояние V’=T(v,r )Состояние vn называется достижимым в системе Σ =(V0,R,T), если существует последовательность {(r0,v0)…(rn,vn}:T(ri,vi)=Vi+1 ∀ i= 0,n-1 Начальное состояние v0 является достижимым по определению.

Состояние системы (F, M) называется безопасным по, если для каждого субъекта, осуществляющего в этом состоянии доступ по

чтению к объекту, уровень безопасности субъекта доминирует над уровнем безопасности объекта:

Состояние (F, M) называется безопасным по записи в случае, если для каждого субъекта, осуществляющего в этом состоянии доступ по записи к объекту, уровень безопасности объекта доминирует над уровнем безопасности субъекта:

Состояние (F, M) называется безопасным, если оно безопасно по чтению и по записи.

Наконец, система Σ =(V0,R,T) называется безопасной, если её начальное состояние v0 безопасно, и все состояния, достижимые из v0 путём применения конечной последовательности запросов из R, безопасны.

Теорема (Основная теорема безопасности Белла-ЛаПадулы). Система Σ =(V0,R,T) безопасна тогда и только тогда, когда выполнены следующие условия: 1. Начальное состояние v0 безопасно. 2. Для любого состояния v, достижимого из v0 путём применения конечной последовательности запросов из R, таких, что T(v,r)=V’, v=(F, M) и V’=(F’,M’) для∀ o∈ O и ∀ s ∈S, выполнены условия:

1. Если r ∈M*[S,O] и r не∈M[S,O] , то F*(O)<=F*(S).

2. Если r∈M[S,O] и F*(S)<=F*(O), то r ∈неM*[S,O]

3. Если w ∈M*[S,O] и wне∈M[S,O] , то F*(S)<=F*(O).

4. Если w∈M[S,O] и F*(O)<=F*(S), то w ∈неM*[S,O]

< Пусть система безопасна. В этом случае начальное состояние v0 безопасно по определению. Предположим, что существует безопасное состояние . v ,достижимое из состояния v: T(v,r) = v* и для данного перехода нарушено одно из условий 1-4. В случае, если нарушены условия 1 или 2, то состояние . v будет небезопасным по чтению, а если нарушены условия 3 или 4 – небезопасным по записи. В обоих случаях мы получаем противоречие с тем, что состояние . v является безопасным.

Докажем достаточность утверждения. Система мб небезопасной в двух случаях:

1. В случае если начальное состояние v0 небезопасно. 2. Если существует небезопасное состояние . v , достижимое из безопасного

состояния v0 путём применения конечного числа запросов из R. Это означает, что на каком-то промежуточном этапе произошёл переход T(v,r) = v* , где v –безопасное состояние, а . v - небезопасное. Однако условия 1-4 делают данный переход невозможным.

Изложенная модель в силу своей простоты имеет целый ряд серьёзных недостатков. Например, никак не ограничивается вид функции перехода T – а это означает, что можно построить функцию, которая при попытке запроса на чтения к объекту более высокого уровня секретности до проверки всех правил будет понижать уровень секретности объекта. Недостаток -потенциальная возможность организации скрытых каналов передачи информации.

В настоящее время модель Белла-ЛаПадулы широко используются при построении и верификации АС.