1.12.5 Поле объемно-заряженного шара

с равномерной плотностью заряда.

Пусть шар радиуса R заряжен с постоянной объемной плотностью . Поле в этом случае обладает центральной симметрией. Легко сообразить, что для поля вне шара получается тот же результат, что и в случае заряженной сферы. Однако для точек внутри шара результат будет иным. Сферическая поверхность радиуса ( ) заключает в себе заряд равный: . Поэтому теорема Гаусса (1.21) для такой поверхности запишется следующим образом:

.

Отсюда, заменив 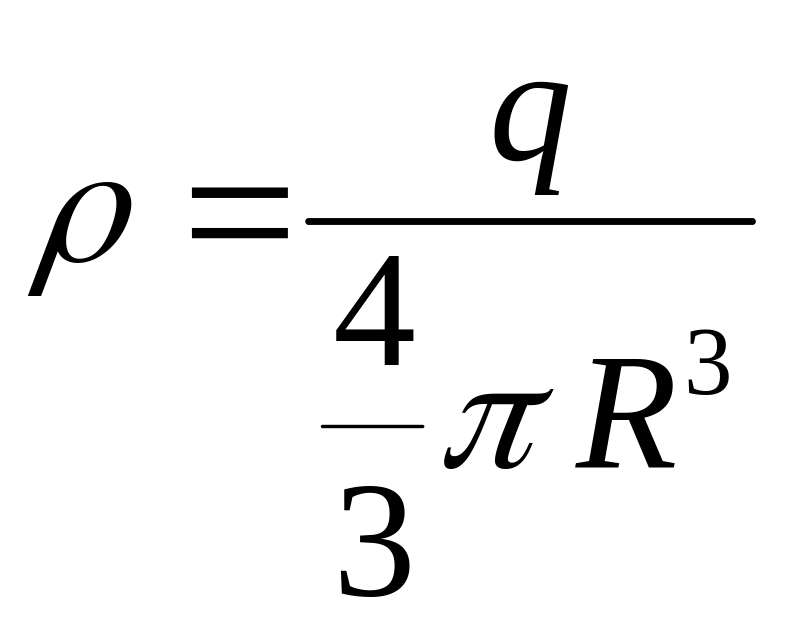, получим

Таким образом, внутри шара напряженность поля растет линейно с расстоянием от центра шара. Вне шара напряженность убывает по такому же закону, как и у поля точечного заряда. В центре шара .

Лекция 3 (2 часа)

Электрический диполь. Диэлектрики в электрическом поле. Сегнетоэлектрики.

( Электрический диполь. Дипольный момент. Момент сил, действующий на диполь в электрическом поле. Сила, действующая на диполь в электричес­ком поле. Энергия диполя во внешнем электрическом поле. Диэлектрики. Полярные и неполярные диэлектрики. Вектор поляризации. Вектор электрического смещения. Диэлектри­ческая восприимчи­вость и проницаемость. Связанные поляризационные за­ряды на поверхности диэлектрика. Обобщение теоремы Гаусса на случай электроста­тических полей в диэлектриках. Сегнетоэлектрики. Пьезоэлек­трический эффект.)

Диполь в однородном и неоднородном электрических полях

Рассмотрим поведение диполя в однородном поле, напряженность которого (рис. 2.3). На заряды диполя действуют равные по величине, но противоположные по направлению силы и . Модуль каждой из сил равен . Эти силы создают момент силы. Умножив его на плечо, получим величину момента сил, действующих на диполь

(2.4)

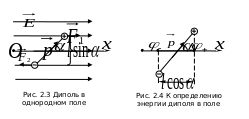
Формула (2.4) может быть записана в векторном виде:

(2.5)

Момент сил (2.5) стремиться повернуть диполь так, чтобы его электрический момент установился по направлению поля.

Диполь в поле обладает энергией, значение которой можно найти по формуле:

(2.6)

Здесь и - значения потенциала внешнего поля в тех точках, где помещаются заряды и .

Потенциал однородного поля уменьшается равномерно в направлении вектора . Приняв это направление за ось ОХ (рис. 2.4), используя (1.6), можно записать .

Из рис. 2.4 видно, что разность равна приращению потенциала на отрезке :

. (2.7)

Подставив (2.7) в формулу (2.6), получим:

, (2.8)

где - угол между векторами и , поэтому (2.80 можно записать в виде:

. (2.9)

Выражение для энергии (2.9) остается справедливым и для неоднородного поля.

Рассмотрим состояние диполя в неоднородном поле. Пусть электрическое поле нарастает вдоль оси ОХ (рис.2.5).

Если угол между векторами и равен нулю (положение 1), то под действием пары сил диполь будет втягиваться в область поля с большей напряженностью .

При начальном угле (положение 2) пара сил, действующих на заряды диполя, будет приводить к его вращению с уменьшением угла и втягиванию в область более сильного поля, то есть к поступательному движению вдоль оси ОХ. При начальном угле диполь будет сначала поворачиваться с уменьшением угла и выталкиваться в область более слабого поля. При достижении угла он поворачивается с уменьшением угла и начинает в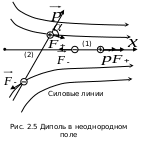 тягиваться в область более сильного поля.

М

О

ожно записать формулу для проекции на ось ОХ силы , вызывающей поступательное движение диполя, используя известное из механики выражение, связывающее консервативную силу и потенциальную энергию:

Итак, при любом начальном угле диполь в неоднородном электрическом поле в итоге втягивается в область более сильного поля. Такое поведение диполя используется в пылеулавливателях: в какой-либо части трубы, из которой выходит дым (это могут быть, например, побочные газообразные продукты горения на тепловых электростанциях, металлургических предприятий), создается неоднородное электрическое поле; частицы дыма (диполи) втягиваются в область более сильного поля и не попадают в атмосферу, не загрязняют окружающую среду.