1.12.3 Поле равномерно заряженной бесконечно длинной прямой нити.

• -Для равномерно заряженной нити во всех её точках линейная плотность заряда 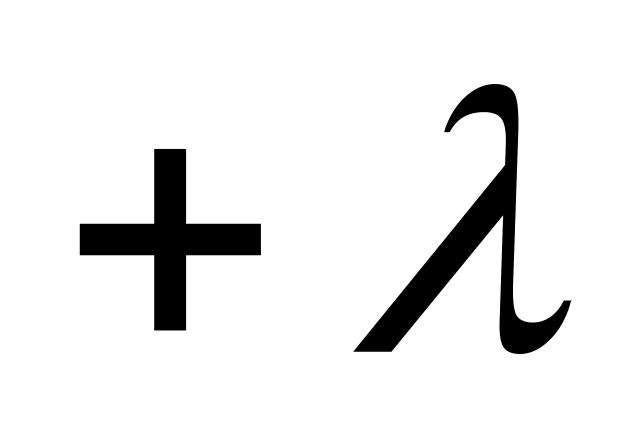будет одинаковой, поэтому поле имеет осевую симметрию: линии вектора представляют собой прямые, выходящие из нити и лежащие в плоскостях, перпендикулярных к ней (рис.1.13 а). На одинаковых расстояниях от нити, т.е. на цилиндрической поверхности, модуль будет одинаковым.

• -Поверхность интегрирования выбирают цилиндрическую, ось которой совпадает с нитью. Поток вектора через основания цилиндра равен нулю (линии напряженности их не пересекают), поэтому остается поток только через боковую поверхность и согласно (1.18) получим:

,

где r радиус цилиндра (расстояние от нити до точки, где определяется напряженность); h – высота цилиндрической поверхности.

• -Определяем заряд внутри цилиндрической поверхности:

.

• Применяем теорему Гаусса (1.21):

, откуда .

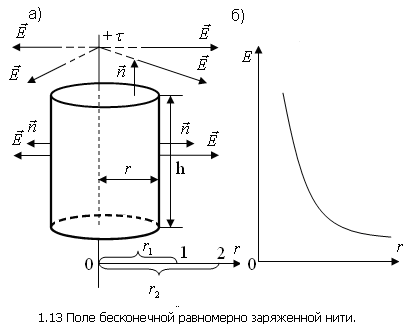
На (рис. 1.13 б) приведен график зависимости модуля вектора от расстояния от нити до точки, в которой он определяется.

Используя связь между потенциалом и напряженностью поля (1.7) можно определить разность потенциалов между двумя точками поля, находящимися на расстояниях и от нити (рис. 1.13 а):

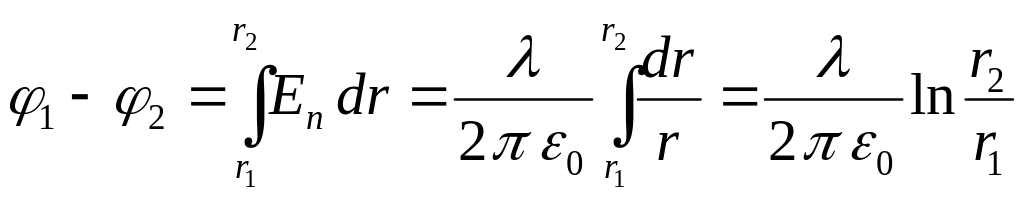
а)
Рис. 1.13 Поле бесконечной равномерно заряженной нити

В заключение отметим, что приведенные выводы справедливы для нити конечной длины при условии, что её длина значительно больше расстояния от нити до точки, в которой определяется напряженность.

1.12.4 Поле равномерно заряженной сферической поверхности радиуса r и заряда q.

• Поле сферической поверхности обладает центральной симметрией – линии вектора представляют собой прямые, выходящие из поверхности, перпендикулярные к ней (рис.1.14). Вне сферы на одинаковых расстояниях от ее центра модуль вектора будет одинаковым.

• Поверхность интегрирования выбираем в виде сферы, центр которой совпадает с центром заряженной сферы (точка О) и имеющей радиус r. Поток вектора через эту сферу (1.18):

; .

	б)
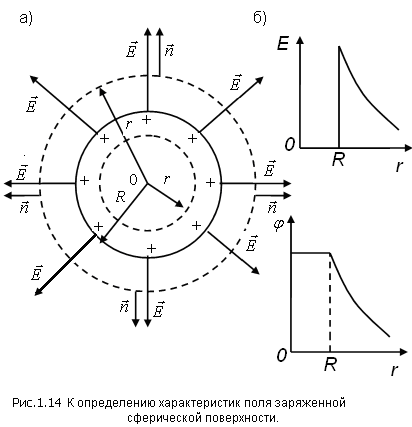
Рис. 1.14 К определению характеристик поля заряженной сферической поверхности: а) равномерно заряженная сферическая поверхность; б) зависимости Е (r ) и φ (r )

• Если 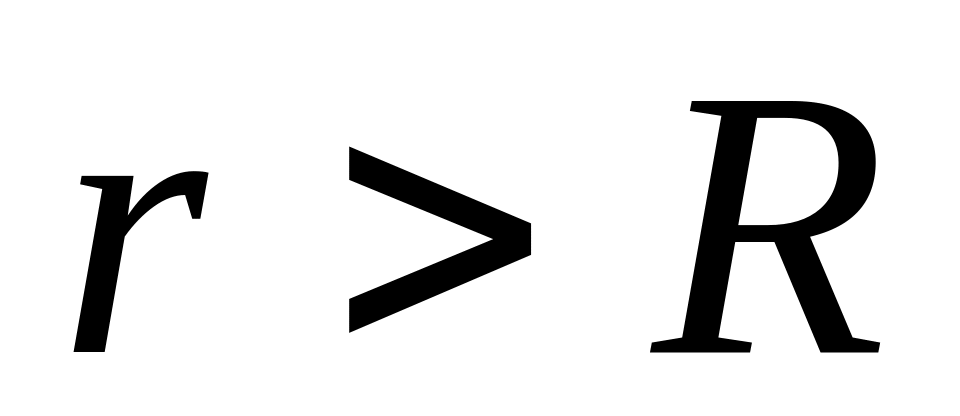, внутрь поверхности попадает весь заряд q, создающий рассматриваемое поле и по теореме Гаусса (1.21):

, откуда ,

• Если 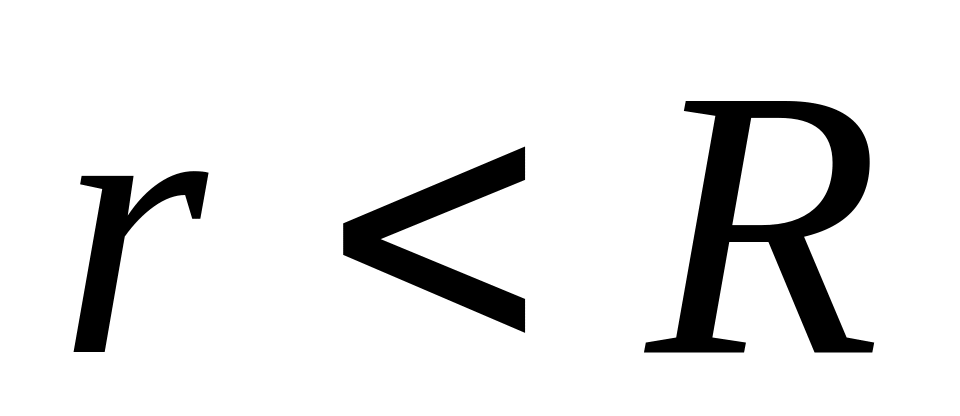, то замкнутая поверхность не содержит внутри зарядов, поэтому внутри равномерно заряженной сферической поверхности электростатическое поле отсутствует.

• Если 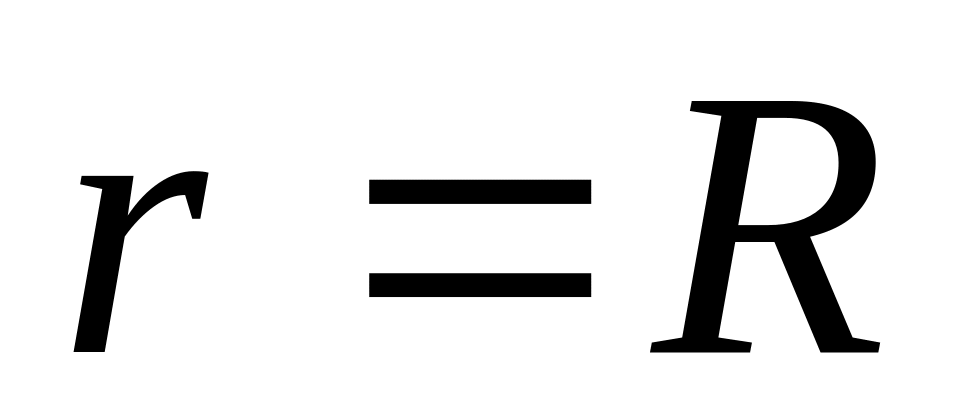справедливы следующие равенства:

где - поверхностная плотность заряда, согласно (1.24):

Т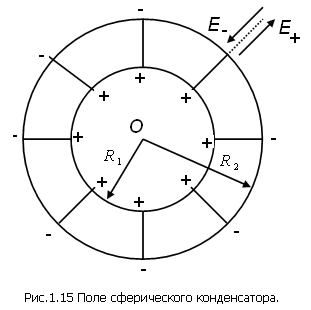 аким образом, можно сделать вывод, что внутри сферы поле отсутствует, а за её пределами оно совпадает с полем точечного заряда q, помещенного в центр сферы.

Г рафики зависимости и от , где - расстояние от центра сферы до точки в которой определяются напряженность и потенциал поля, приведены на рис. 1.14 б.

С

Рис. 1.15 Поле сферического конденсатора

помощью принципа суперпозиции легко определить поле двух сферических поверхностей, имеющих общий центр (точка O, рис. 1.15.), которые заряжены одинаковыми по величине, но различными по знаку зарядами. Такая система называется сферическим конденсатором. В общей внутренней части меньшей и большей сфер поле отсутствует. В зазоре между поверхностями напряженность поля Е определяется по формуле:

,

где .

Разность потенциалов между сферами определяется по формуле (1.8): .

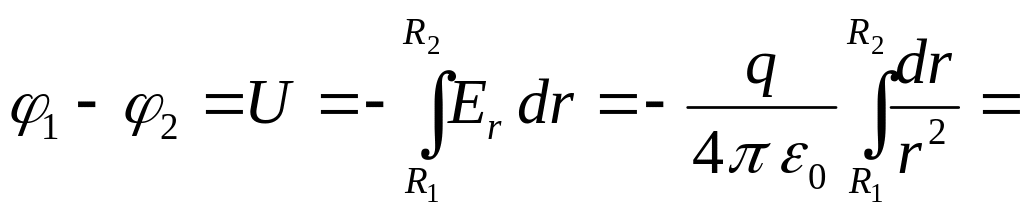
Поле сферического конденсатора в отличие от поля плоского является неоднородным.