1.8 Связь между напряжённостью поля и потенциалом (градиент потенциала)

Пусть имеется произвольное электростатическое поле. В этом

п оле проведём две эквипотенциальные поверхности таким образом, что они отличаются одна от другой потенциалом на величину dφ (рис. 1.7)

Вектор напряжённости направлен по нормали к поверхности . Направление нормали совпадает с направлением оси x.

Ось x, проведённая из точки 1, пересекает поверхность в точке 2.

Отрезок dx представляет собой кратчайшее расстояние между точками 1 и 2. Работа, совершаемая при перемещении заряда вдоль этого отрезка:

.

С другой стороны, эту же работу можно записать как:

.

Приравнивая эти два выражения, получим:

, (1.6)

где символ частной производной подчёркивает, что дифференцирование производиться только по x. Повторив аналогичные рассуждения для осей y и z, можем найти вектор :

, (1.7)

где – единичные векторы координатных осей x, y, z.

Вектор, определяемый выражением (1.7) называется градиентом скаляра φ. Для него наряду с обозначением применяется также обозначение . («набла») означает символический вектор, называемый оператором Гамильтона

Следовательно, из определения градиента можно записать:

т.е. напряжённость поля равна градиенту потенциала со знаком минус. Знак минус определяется тем, что вектор напряжённости поля направлен в сторону убывания потенциала.

По формуле 1.7 можно найти проекцию вектора на выбранное направление в пространстве, например на ось x:

, или 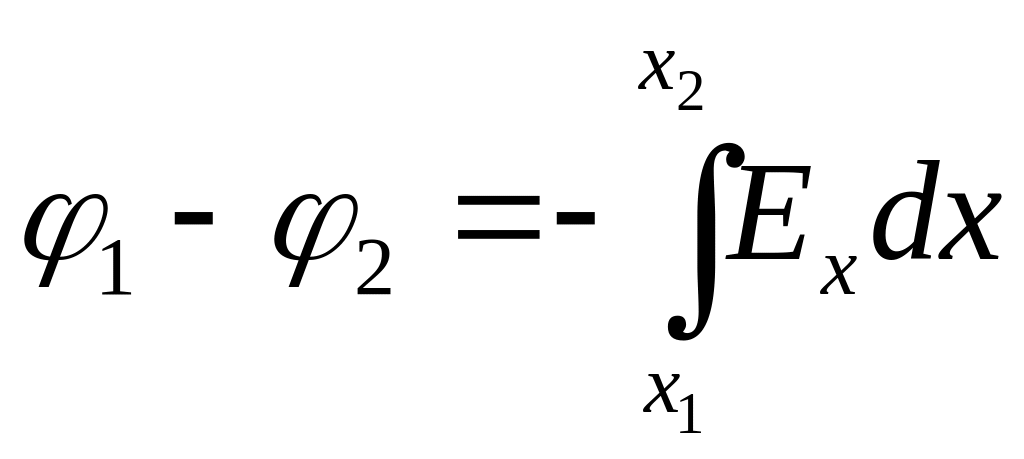, (1.8)

где ( ) − разность потенциалов между точками 1 и 2, расположенными на оси x.

Лекция 2 (2 часа)

Потенциал электрического поля.

(Работа сил электростатического поля по перемещению электрического заряда. Потенциальная энергия заряда в электростатическом поле. Циркуляция вектора напряженности. Теорема о цирку­ляции напряженности электростати­ческого поля в интегральной и дифференциальной форме. Потенциал электростатического поля. Напряженность как градиент потенциала. Эквипотенциальные поверхности. Вычисление потенциала по напряженности поля.)

Работа, совершаемая при перемещении заряда в электростатическом поле. Теорема о циркуляции вектора напряжённости электростатического поля

Предположим, что некоторый точечный заряд перемещается в поле неподвижного точечного заряда из точки 1 в точку 2 (рис. 1.8). На заряд действует сила, и, следовательно, совершается работа. Первоначально определим работу на малом перемещении :

или ,

где – проекция вектора силы на направление перемещения .

Следовательно, , но , где равно приращению модуля радиуса-вектора , поэтому . Так как заряды точечные, то

Р абота, совершаемая при перемещении заряда из точки 1 в точку 2, определится выражением:

, (1.9)

или после интегрирования 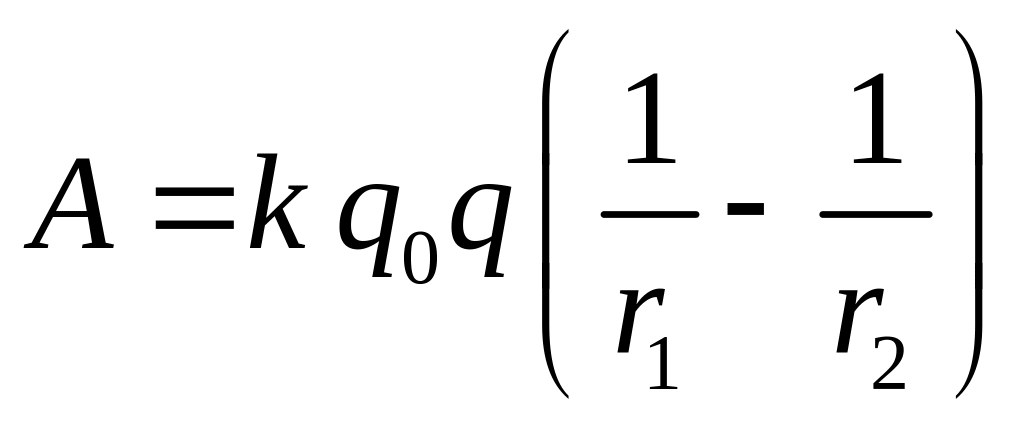(1.10)

Из выражения (1.10) можно сделать следующие выводы:

– работа не зависит от формы траектории, по которой движется заряд q_0,, зависит от положения начальной 1 и конечной 2 точек перемещения. Силовые поля, удовлетворяющие этому условию, называют потенциальными, а силы, действующие в этих полях называют консервативными. Следовательно, электростатическое поле потенциально, а силы в этом поле консервативны.

– Работа, совершаемая при перемещении заряда q₀ вдоль замкнутой траектории (r₁ = r₂) равна нулю.

Если силовые линии замкнуты, то такое поле называется вихревым. К таким полям относятся магнитное и возбуждаемое переменным магнитным электрическое.

Работу, совершаемую при перемещении заряда в поле вдоль замкнутого контура можно определить выражением:

, так как

Согласно выражению (1.8) эта работа равна нулю и следовательно:

(1.11)

Выражение называют циркуляцией вектора напряжённости электростатического поля, а (1.11) теоремой о циркуляции .

Выражение (1.11) позволяет решать многие задачи, связанные с электростатическим полем.