1.5 Принцип суперпозиции электростатических полей

Если в данной точке пространства различные заряженные тела создают поля с напряженностями , и т.д., то результирующая напряженность поля в этой точке равна:

где N – число зарядов, создающих систему.

Это утверждение называют принципом суперпозиции электрических полей. Он вытекает из принципа суперпозиции сил в механике.

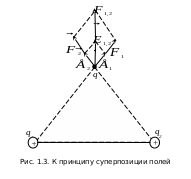
Покажем это на примере двух зарядов q₁ и q₂ (рис. 1.3).

Эти заряды создают вокруг себя электрические поля с напряженностями и соответственно. На внесённый заряд со стороны этих полей действуют силы и соответственно:

Результирующая сила :

Результирующая напряженность поля будет равна:

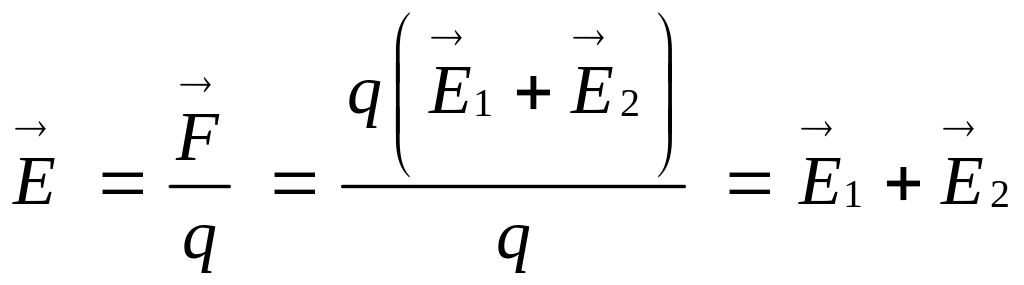
Абсолютная величина вектора может быть рассчитана по теореме косинусов:

где – угол между векторами и .

Итак, если электростатическое поле создано не одним, а несколькими зарядами, то напряжённость такого поля равна векторной сумме напряжённостей полей, создаваемых в данной точке каждым из зарядов в отдельности.

1.6 Силовые линии электростатического поля

Непрерывные линии, касательные к которым в каждой точке, через которую они проходят, совпадают с вектором напряженности, называются силовыми линиями электрического поля или линиями напряженности.

В действительности силовых линий не существует, это просто графический метод исследования электростатических полей.

Силовые линии наделены следующими свойствами:

– Силовые линии электростатического поля не замкнуты ‑ они начинаются на положительных и заканчиваются на отрицательных зарядах.

– Линии непрерывны и нигде не пересекаются (т.к. их пересечение означало бы отсутствие определенного направления напряженности электрического поля в данной точке).

– Густота линий выбирается так, чтобы количество линий, пронизывающих единицу поверхности площадки, перпендикулярной к линиям, было равно численному значению (модулю) вектора .

Т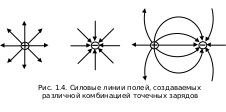 ак как силовые линии начинаются или оканчиваются на заряженных телах, а затем расходятся в разные стороны, то густота линий больше вблизи заряженных тел. Следовательно, вблизи заряженных тел напряженность поля больше, чем в более удалённых точках.

– Общее число силовых линий пересекающих некоторую поверхность иначе называют потоком вектора напряжённости поля.

На рис. 1.4 приведены силовые линии точечных положительного и отрицательного зарядов и электрического диполя (системы двух зарядов).

С графическим изображением полей, создаваемых более сложной системы зарядов можно познакомиться в лаборатории виртуального практикума кафедры «Физика».

1.7 Эквипотенциальные поверхности

Для более наглядного графического изображения полей кроме линий напряжённости используют поверхности равного потенциала или эквипотенциальные поверхности. Как следует из названия, эквипотенциальная поверхность – это такая поверхность, все точки которой имеют одинаковый потенциал. Если потенциал задан как функция x, y, z, то уравнение эквипотенциальной поверхности имеет вид:

.

Л инии напряжённости поля перпендикулярны эквипотенциальным поверхностям.

Докажем это утверждение.

Пусть линия и силовая линия составляют некоторый угол (рис. 1.5).

Переместим из точки 1 в точку 2 вдоль линии пробный заряд . При этом силы поля совершают работу:

. (1.5)

Т.е. работа перемещения пробного заряда вдоль эквипотенциальной поверхности равна нулю. Эту же работу можно определить и другим способом – как произведение заряда на модуль напряженности поля, действующего на пробный заряд, на величину перемещения и на косинус угла между вектором и вектором перемещения , т.е. косинус угла (рис. 1.5):

.

Величина работы не зависит от способа её подсчёта, согласно (1.5) она равна нулю. Отсюда вытекает, что и, соответственно , что и требовалось доказать.

Э

квипотенциальную поверхность можно провести через любую точку поля. Следовательно, таких поверхностей может быть построено бесконечное множество. Условились, однако, проводить поверхности

т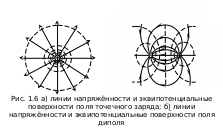 аким образом, чтобы разность потенциалов для двух соседних поверхностей была бы всюду одна и та же. Тогда по густоте эквипотенциальных поверхностей можно судить о величине напряжённости поля. Действительно, чем гуще располагаются эквипотенциальные поверхности, тем быстрее изменяется потенциал при перемещении вдоль нормали к поверхности.

На рис. 1.6 (а) показаны эквипотенциальные поверхности (точнее, их пересечения с плоскостью чертежа) для поля точечного заряда. В соответствии с характером изменения эквипотенциальные поверхности при приближении к заряду становятся гуще.

На рис. 1.6 (б) изображены эквипотенциальные поверхности и линии напряжённости для поля диполя.

Из рис. 1.6 видно, что при одновременном использовании эквипотенциальных поверхностей и линий напряжённости картина поля получается особенно наглядной.

Для однородного поля эквипотенциальные поверхности, очевидно, представляют собой систему равноотстоящих друг от друга плоскостей, перпендикулярных к направлению напряжённости поля.