Энергия электростатического поля.

(Энергия системы зарядов. Энергия заряженного уединенного проводника. Энергия заряженного конденсатора. Сила взаимодействия между пластинами плоского конденсатора. Энергия элек­трического ноля. Объемная плотность энергии электрического поля.)

Энергия электростатического поля Энергия системы зарядов.

Получим выражение для потенциальной энергии системы двух точечных зарядов и , находящихся на расстоянии . Когда заряды удалены друг от друга на бесконечность, они не взаимодействуют и энергия в этом случае равна нулю. При сближении зарядов на расстояние совершается работа против сил электрического поля, которая идет на увеличение потенциальной энергии системы. Сближение зарядов можно произвести, приближая к ,или к .Работа переноса заряда из бесконечности в точку, удаленную от на , равна

,

где - потенциал, создаваемый зарядом в той точке, в которую перемещается заряд . Аналогично работа переноса заряда из бесконечности в точку, удаленную от на , равна

,

где - потенциал, создаваемый зарядом в той точке, в которую перемещается заряд . Значение работ в обоих случаях одинаково, и каждое из них выражает энергию системы: .

Для того чтобы в выражение энергии системы оба заряда входили симметрично, запишем его следующим образом:

(5.1)

Формула (5.1) задает энергию системы двух зарядов. Перенесем из бесконечности еще один заряд и поместим его в точку, находящуюся на расстоянии от и от . При этом совершается работа

,

где - потенциал, создаваемый зарядами и в той точке, в которую перемещается заряд .В сумме с и работа будет равна энергии трех зарядов:

(5.2)

Выражение (5.2) можно привести к виду:

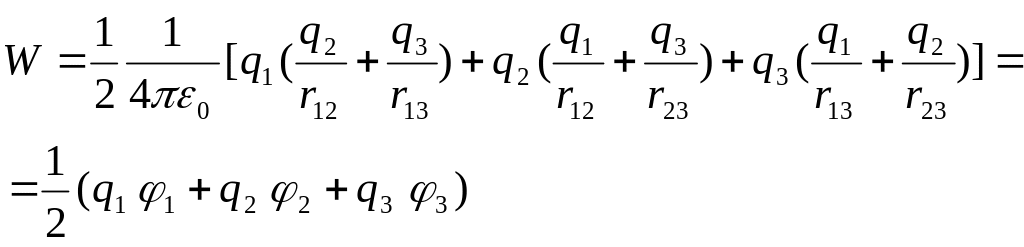
Добавляя к системе зарядов последовательно и т.д., можно убедиться в том, что в случае N зарядов потенциальная энергия системы равна:

(5.3)

где - потенциал, создаваемый в той точке, где находится , всеми зарядами, кроме k-го.

5.2 Энергия заряженного проводника.

Заряд q, находящийся на некотором проводнике, можно рассматривать как систему точечных зарядов, а, следовательно, энергия заряженного проводника может быть определена по формуле (5.3). Известно, что область, занятая проводником является эквипотенциальной, поэтому . Вынесем в формуле (5.3) за знак суммы:

так как и определяет весь заряд, сосредоточенный на проводнике, выражение для энергии заряженного проводника получим в виде: .

Применяя соотношение , можно получить следующие выражения для потенциальной энергии заряженного проводника:

5.3 Энергия заряженного конденсатора

Пусть заряд находится на обкладке с потенциалом , а заряд на обкладке с потенциалом . Согласно формуле (5.3) энергию такой системы можно определить:

(5.4)

Воспользовавшись выражением (3.4) для электроемкости конденсатора (5.4) можно представить в виде:

(5.5)

5.4 Энергия электростатического поля.

Энергию заряженного конденсатора можно выразить через величины, характеризующие поле между пластинами. Сделаем это для плоского конденсатора. Учитывая (3.4) и что , (5.5) примет вид:

(5.6)

Так как - объем, занимаемый полем, то формулу (5.6) можно записать в виде:

(5.7)

Формула связывает энергию конденсатора с зарядом на его обкладках, а формула (5.7) – с напряженностью поля. В рамках электростатики невозможно ответить на вопрос, что является носителем энергии – заряды или поле? Постоянные поля и создающие их заряды не могут существовать обособленно друг от друга. Законы электродинамики доказывают, что носителем энергии является поле.

Если поле однородно (например, в плоском конденсаторе) энергия в нем распределяется с постоянной плотностью, значение которой можно найти по формуле:

. (5.8)

С учетом взаимосвязи напряженности и индукции поля , выражения для плотности энергии (5.8) можно записать следующим образом:

.

Принимая во внимание(2.7), получим:

(5.9)

Первое слагаемое в (5.9) определяет плотность энергии в вакууме, а второе – определяет плотность энергии, затрачиваемую на поляризацию диэлектрика.

Лекция 6 (2 часа)