4.2 Незаряженный проводник во внешнем электрическом поле.

П

оместим во внешнее электрическое поле напряжённости незаряженный проводник.

П од действием сил поля свободные заряды в проводнике приходят в движение: положительные по полю, а отрицательные против поля.

На одном конце проводника будет скапливаться избыток положительного, а на другом избыток отрицательного заряда. Эти заряды называются индуцированными. Процесс будет происходить до тех пор, пока напряженность поля внутри проводника не станет равной нулю, а линии напряженности вне проводника – перпендикулярными его поверхности (рис. 4.4). Пунктиром показаны линии напряженности до внесения проводника в поле, а сплошные – линии напряженности после внесения. Таким образом, нейтральный проводник, внесенный в электростатическое поле, разрывает часть линий напряженности; они заканчиваются на отрицательных индуцированных зарядах и вновь начинаются на положительных. Индуцированные заряды распределяются на внешней поверхности проводника. Явление перераспределения поверхностных зарядов на проводнике во внешнем электростатическом поле называется электростатической индукцией.

Если внутри проводника имеется полость, то при равновесном распределении индуцированных зарядов поле внутри нее также равно нулю.

Итак, внешнее электрическое поле не проникает внутрь металла. Это позволяет, например, использовать металлическую оболочку, сплошную или в виде сетки, для защиты (экранировки) различных приборов от внешних электрических полей.

4.3 Электроёмкость проводника

Рассмотрим уединённый проводник, т.е. проводник который удалён от других тел. Его потенциал, согласно (1.15), прямо пропорционален заряду проводника. Из опыта следует, что разные проводники, будучи одинаково заряженными, имеют различные потенциалы. Поэтому для уединённого проводника можно записать:

.

Величину

(4.3)

называют электроёмкостью (или просто ёмкостью) уединённого проводника. Емкость уединённого проводника определяется зарядом, сообщение которого проводнику изменяет его потенциал на единицу.

Емкость проводника зависит от его размеров и формы, но не зависит от материала, агрегатного состояния, формы и размеров полостей внутри проводника. Это связано с тем, что избыточные заряды распределяются на внешней поверхности проводника.

Единица электроёмкости – фарад (Ф); 1 Ф – емкость такого уединённого проводника, потенциал которого изменяется на 1В при сообщении ему заряда 1 Кл.

Потенциал уединённого шара радиуса R, находящегося в однородной среде с диэлектрической проницаемостью ε, равен:

,

используя формулу (4.3) получим, что емкость шара

Отсюда следует, что емкостью 1 Ф обладал бы уединённый шар, находящийся в вакууме и имеющий радиус км, что примерно в 1400 раз больше радиуса Земли (электроёмкость Земли С≈0.7 мФ). Следовательно, фарад – очень большая величина, поэтому на практике используются дольные единицы – миллифарад (мФ), микрофарад (мкФ) и др.

4.4 Конденсаторы. Электроёмкость конденсаторов.

Наибольший эффект увеличения электроёмкости проводника достигается для конденсаторов, представляющих собой две металлических пластины, разделённые слоем диэлектрика. На пластины (обкладки) подают заряды, одинаковые по модулю и противоположные по знаку. Форма конденсатора обеспечивает существование электрического поля только в пространстве между ними. Это позволяет устранить влияние на электроёмкость конденсатора окружающих его тел.

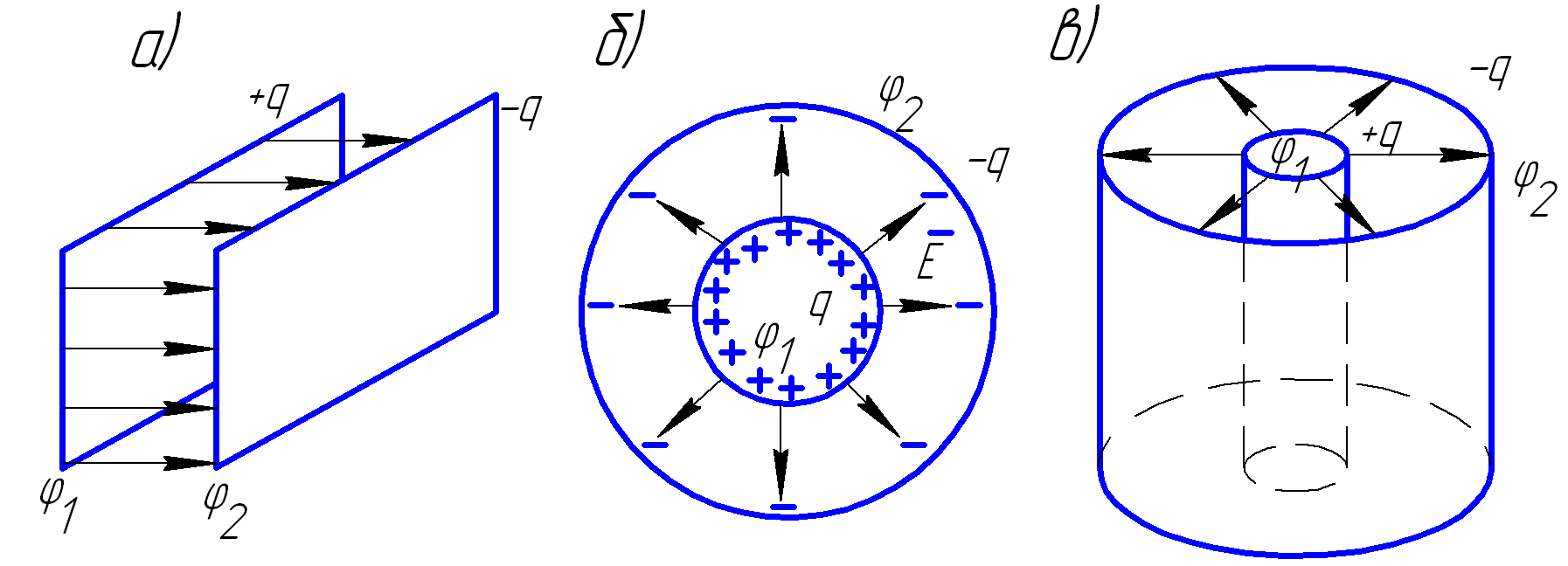
На рис. 4.5 приведено схематическое изображение плоского, сферического и цилиндрического конденсаторов.

Электроёмкость конденсатора вводится формулой

(4.4)

где q – заряд положительно заряженной пластины конденсатора, - разность потенциалов между его обкладками.

б)

Рис. 4.5 Виды конденсаторов: а) плоский; б) сферический; в) цилиндрический

Электроёмкость конденсатора, как и электроёмкость уединённого проводника, зависит только от его геометрических размеров и диэлектрических свойств среды между его пластинами.

Запишем формулы для электроёмкости конденсаторов различного вида:

а) Плоский конденсатор. Из формул (4.4) и (1.27) получим:

где S – площадь одной пластины конденсатора, d – расстояние между ними, ε – относительная диэлектрическая проницаемость среды между обкладками конденсатора.

б) Сферический конденсатор. Радиусы обкладок обозначим R₁ и R₂ ( ). Электрическое поле конденсатора обладает сферической симметрией и, согласно теореме Гаусса, определяется зарядом только внутренней сферы. Учитывая формулу разности потенциалов между обкладками конденсатора (1.28), получим:

в) Электроёмкость цилиндрического конденсатора:

,

где h – высота конденсатора, R₁ и R₂ – радиус внутренней и внешней поверхностей.

Лекция 5 (2 часа)