1.6. Связь между линейными и угловыми величинами

Обратимся к рис. 1.4 и формуле (1.9). Для того чтобы связать линейную скорость произвольной точки А твердого тела с угловой скоростью вращения этого тела вокруг неподвижной оси ОО’, поделим обе части формулы на . Учитывая, что и , получим

, (1.10)

т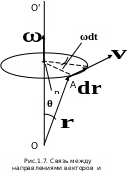 .е. линейная скорость вращающейся точки равна векторному произведению угловой скорости на радиус-вектор этой точки (рис.1.7). Модуль вектора (1.10) равен , где – радиус окружности, по которой движется точка А. Подставляя это выражение в формулы (1.2) и (1.3), получим и , откуда модуль полного ускорения согласно (1.4) равен

.

Лекция 2 (2 часа)

Динамика матери­аль­ной точки.

(Динамика материальной точки. Инерци­альные и неинерциальные системы отсчета. Законы Ньютона и их физическое содержание. Масса, вес, сила, импульс силы. Импульс материальной точки. Полный импульс системы материальных точек. Закон сохранения импульса. Движение тела с переменной массой. Центр масс. Теорема о движение центра масс.)

Первый закон Ньютона. Инерциальные системы отсчета

Динамика – раздел механики, в котором изучаются законы движения тел и причины, вызывающие изменение характера их движения. В основе динамики лежат три закона, сформулированные в конце 17-го века И. Ньютоном. Эти законы не выводятся, а являются обобщением накопленного многовекового человеческого опыта. Их следует рассматривать в совокупности как систему взаимосвязанных законов, а не каждый закон в отдельности.

Первый закон утверждает, что существуют такие системы отсчета, в которых всякое тело сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействия со стороны других тел не заставят его изменить это состояние.

Движение тел в отсутствие внешних воздействий называется движением по инерции, при этом проявляется особое динамическое свойство тел – инертность. Соответственно, первый закон Ньютона называют законом инерции, а системы отсчета, в которых он выполняется, называют инерциальными системами отсчета (ИСО). Все системы отсчета, которые можно считать инерциальными, должны двигаться друг относительно друга равномерно и прямолинейно.

В настоящее время экспериментально с большой точностью установлено, что практически идеально инерциальной является гелиоцентрическая система отсчета, начало координат которой находится в центре инерции (см. далее) Солнечной системы (приближенно – в центре Солнца), а оси координат проведены взаимно перпендикулярно в направлении трех удаленных звезд.

Для ИСО в рамках классической механики (т.е. для макроскопических тел, движущихся со скоростями, значительно меньшими скорости света) справедлив принцип относительности Галилея, согласно которому все ИСО по своим механическим свойствам эквивалентны друг другу. Это значит, что во всех ИСО одинаковы свойства пространства (однородность и изотропность) и времени (однородность), а также одинаково выполняются все законы механики.

Непосредственно из принципа относительности вытекают так называемые преобразования Галилея для координат и скоростей при переходе от одной ИСО к другой. Пусть инерциальная система K' движется с постоянной скоростью (она называется переносной) относительно другой инерциальной системы K (рис. 2.1). Для упрощения выберем оси координат X’, Y’, Z’ системы K’ параллельно соответствующим осям X, Y, Z системы K, причем так, чтобы оси Х и Х' совпадали друг с другом и были направлены вдоль вектора . Очевидно, если взять за начало отсчета времени момент, когда начала координат О и О' совпадали, то связь между радиусами-векторами и одной и той же точки А в K- и K’- cистемах может быть записана:

(2.1)

и, кроме того,

.

При этом подразумевается абсолютность пространства и времени, т.е. одинаковость длин отрезков и хода времени во всех ИСО. Продифференцировав (2.1) по времени, найдем классический закон преобразования скорости:

. (2.2)

Дифференцируя это выражение по времени с учетом постоянства скорости , получим , т.е. ускорение материальной точки одинаково во всех ИСО.