1.5. Основное уравнение молекулярно-кинетической теории идеальных газов

Важной задачей МКТ является установление связи между микроскопическими параметрами газа (массой, скоростью, импульсом, кинетической энергией молекул) и его макроскопическими параметрами (температурой, давлением и объемом). Эту взаимосвязь устанавливает основное уравнение МКТ.

Рассмотрим идеальный газ, который в объеме содержит молекул, движущихся со скоростями . Введем среднюю квадратичную скорость

, (20)

которая характеризует всю совокупность молекул газа.

Основное уравнение молекулярно-кинетической теории идеальных газов имеет вид:

. (21)

Тепловое движение молекул характеризуется средней кинетической энергией молекулы

. (22)

Тогда уравнение (21) с учетом (22) примет вид:

. (23)

Если вместо концентрации молекул использовать выражение , где ‑ плотность газа, то уравнение (21) примет вид:

. (24)

Если вместо концентрации молекул использовать выражение , то уравнение (23) примет вид:

.

Далее, произведение можно представить в виде:

.

где ‑ кинетическая энергия всех молекул газа. В этом случае уравнение (23) перепишем как:

.

Сравнив это уравнение с уравнением Менделеева-Клапейрона, можно записать:

. (25)

То есть общая кинетическая энергия всех молекул прямо пропорциональна температуре.

Преобразуем выражение для средней энергии одной молекулы следующим образом:

, или

. (26)

Исходя из выражения (26), можно найти среднюю квадратичную скорость молекул:

. (27)

Из уравнения (26) следует, что термодинамическая температура является количественной мерой энергии поступательного движения молекул идеального газа.

При одинаковой температуре средние кинетические энергии молекул всех газов одинаковы, несмотря на различие масс молекул разных газов.

При температуре абсолютного нуля в случае идеального газа согласно выражению (26) средняя кинетическая энергия молекулы . То есть при прекращается поступательное движение молекул газа, а следовательно, его давление равно нулю. Но это не означает, что при абсолютном нуле температуры прекращается всякое движение вообще. Ведь при этом остается движение электронов в атоме, нуклонов в ядре, движение элементарных частиц и так далее.

Лекция 15 (2 часа)

Физические основы молекулярно-кинети­ческой теории газов

(Распределение молекул по скоростям. Экспериментальная проверка распределения Максвелла. Барометрическая формула. Распределение Больцмана. Опыты Перрена. Средняя длина свободного пробега молекул. Число столкновений. Зависимость средней длины свободного пробега от концентрации и эффективного диаметра молекул)

Закон Максвелла о распределении молекул по скоростям

Если газ находится в равновесии, молекулы движутся хаотически, и все направления их движения равновероятны. Скорости молекул могут быть самыми различными по модулю и при каждом соударении с другими молекулами изменяются случайным образом.

В газе, находящемся в состоянии равновесия, устанавливается стационарное распределение молекул по скоростям, подчиняющееся определенному статистическому закону. Этот закон был выведен теоретически Дж. Максвеллом. Максвелл предполагал, что вещество состоит из очень большого числа тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Также предполагалось, что силовые поля на газ не действуют.

Закон Максвелла описывается некоторой функцией , называемой функцией распределения молекул по модулям скоростей. Если разбить диапазон скоростей молекул на малые интервалы, равные , то на каждый интервал скорости будет приходиться некоторое число молекул , скорости которых заключены в этом интервале.

Функция определяет относительное число молекул , скорости которых лежат в интервале от до , то есть

, откуда . (28)

Применяя методы теории вероятностей, Дж. Максвелл нашел вид функции распределения молекул идеального газа по модулям скоростей хаотического движения:

. (29)

Из (29) следует, что конкретное распределение зависит от рода газа (от массы молекулы ) и от его термодинамической температуры. Очевидно, что функция распределения не зависит ни от давления, ни от объема газа. График функции распределения имеет вид, показанный на рис. 5.

В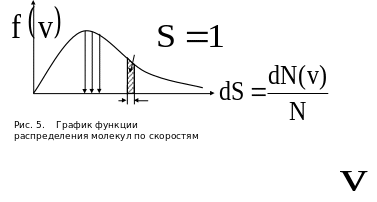 ыражение представляет собой вероятность встретить молекулу со скоростью, принадлежащей интервалу . Эта вероятность равна площади заштрихованной полоски с основанием (рис. 5). Относительная доля молекул, имеющих определенную скорость, равна нулю.

Площадь под кривой равна вероятности достоверного события – встретить молекулу со скоростью, принадлежащей интервалу , то есть равна единице. Это означает, что функция удовлетворяет условию нормировки:

(30)

Наиболее вероятная , средняя арифметическая и

среднеквадратичная скорости молекул

Наиболее вероятная скорость соответствует максимуму функции распределения, ведь именно этой скоростью будет обладать наибольшее число молекул. Ее значение найдется из условия экстремума функции :

.

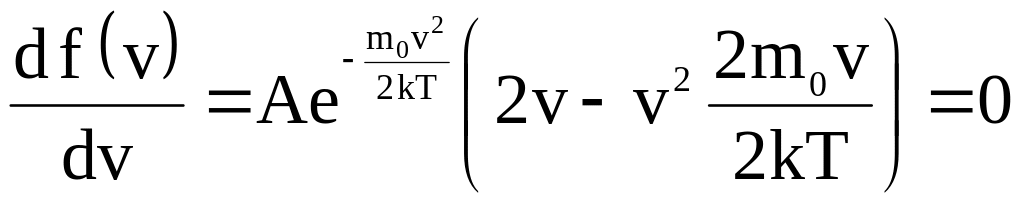. (31)

О тсюда видно, что при увеличении температуры максимум кривой распределения сместится вправо, так как при увеличении увеличивается , которая определяет положение максимума. Но площадь под кривой должна оставаться постоянной. Поэтому величина максимума будет уменьшаться. Влияние же массы молекулы будет обратным. Влияние температуры и массы молекулы на вид функции распределения показано на рис. 6.

Выражение для средней скорости определяется по формуле

. (32)

Аналогично найдем выражение для среднеквадратичной скорости:

.

Произведя интегрирование, получим:

. (33)

Из сравнения найденных скоростей вытекает:

.

Соотношения между скоростями:

При комнатной температуре средняя арифметическая скорость молекул кислорода будет равна:

.

Первое экспериментальное определение скоростей молекул было осуществлено Штерном в 1920 г: подтвердилась правильность оценки средней скорости молекул, вытекающей из распределения Максвелла; о характере распределения этот опыт дал лишь приближенные сведения. Более точно закон Максвелла был проверен в опыте Ламмерта (1929 г.).

Из функции распределения молекул по модулям скоростей можно получить функцию распределения молекул по кинетическим энергиям теплового движения:

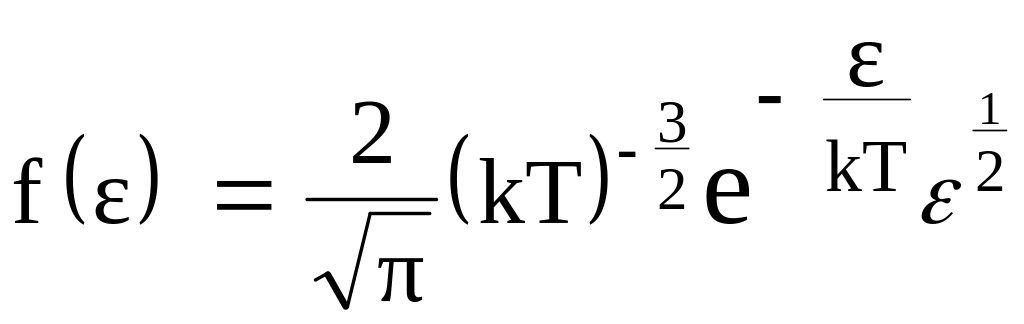. (34)

Найдем среднюю кинетическую энергию молекулы идеального газа:

(35)