Пространственно-временные соотноше­ния и их следствия. Понятие о релятивист­ской механике.

(Основы релятивисткой механики. Постулаты специальной теории относительности. Постоянство скорости света в различных системах отсчета. Преобразования Галилея. Преобразования Лоренца. Релятивистское изменение длин и промежутков времени. Релятивистский закон сложения скоростей. Основной закон релятивистской динамики. Закон изменения массы со скоростью. Взаимосвязь массы и энергии в специальной теории относительности.)

Известно, что механические волны, в частности звук, распространяются в какой-либо среде. В вакууме механические волны не распространяются.

Поэтому, когда было установлено, что свет (в частности и от звезд) ‑ это электромагнитные волны, естественно возникло представление о том, что и свет распространяется в некоторой среде, которую назвали эфиром. Вслед за этим возникла необходимость определить характеристики этого эфира.

Кроме того, необходимо было решить и фундаментальный вопрос о движении эфира. Здесь предоставляются три возможности.

1). Эфир совершенно не увлекается материальными телами при их движении. Тогда с эфиром можно связать абсолютную систему отсчета и уже относительно нее определять движение всех других систем отсчета.

2). Эфир частично увлекается материальными телами при их движении.

3). Эфир полностью увлекается материальными телами.

Рассмотрим экспериментальные данные относительно этой проблемы физики.

Звездная аберрация

Р ассмотрим так называемую звездную аберрацию ‑ смещение углового положения звезд на небесном своде за счет орбитального движения Земли (см. рис. 1.26).

Пусть телескоп ‑ труба длиной со входным и выходным отверстиями ‑ направлен точно на звезду . Если Земля неподвижна относительно звезды, то луч света пройдет через телескоп и попадет на приемник света.

Если Земля движется со скоростью , то луч света не попадет на приемник, так как за то время , которое луч света идет от объектива до окуляра

где с ‑ скорость света, приемник света сместится на расстояние , равное

Следовательно, для того, чтобы луч света попал на приемник, необходимо телескоп наклонить на угол по ходу движения Земли (см. рис. 1.26). Этот угол определится из условия:

Поскольку скорость движения Земли по орбите много меньше скорости света , то тангенс угла можно заменить самим углом:

Через полгода, направление скорости Земли изменится на противоположное, и телескоп нужно наклонять в другую сторону под тем же углом . Полный угол аберрации будет, очевидно, равен:

Т.о., вследствие движения Земли по орбите, положение звезд на небесной сфере мы можем указать лишь с точностью до угла аберрации.

Были произведены измерения углов аберрации для некоторых звезд. А зная угол аберрации и орбитальную скорость Земли, можно определить скорость света.

Измерения дают для скорости света , что весьма близко к действительности.

Значение аберрации звезд двоякое.

1). Оно дает то же значение скорости света, что и измеренное в земных условиях и из экспериментов за наблюдением движения спутников Сатурна

и говорит о постоянстве скорости света.

2). Оно опровергает гипотезу полностью увлекающегося эфира, т.к. в этом случае ни о какой аберрации не могло быть и речи ‑ свет распространялся бы в эфире, неподвижном по отношению к телескопу (Земле).

Остается предположить, что эфир либо частично, либо вовсе не увлекается материальными телами.

Опыты Майкельсона

В 1887 году Майкельсоном был поставлен специальный эксперимент по проверке этой гипотезы. Идея эксперимента Майкельсона состоит в следующем.

Р ассмотрим интерферометр, с взаимно перпендикулярными плечами (см. рис. 1.27). Плечи интерферометра и равны друг другу. Разность хода лучей и возникает вследствие того, что луч дважды проходит через пластинку , а луч ‑ один раз. Сама пластинка прозрачная, отражающая 50% падающего на нее света и пропускающая, соответственно, 50% света. Как известно, если разность хода между лучами и равна четному числу полуволн ‑ то выполняется условие максимума, и мы будем видеть в микроскоп пластинку светлой. Если же разность хода равна нечетному числу полуволн, то выполняется условие минимума, и мы будем видеть пластинку темной.

Однако, такое наблюдение неудобно. Поэтому зеркало ставят под небольшим углом, тогда интерференционная картина будет иметь вид полос равной толщины.

И при незначительном изменении разности хода эта система интерференционных полос будет смещаться относительно своего нулевого положения.

Такова будет схема интерференционных лучей в интерферометре, неподвижном относительно гипотетического эфира.

Предположим теперь, что интерферометр движется вместе с Землей относительно эфира со скоростью Земли в направлении плеча . Тогда, если раньше время хода луча было:

где ‑ длина плеча интерферометра, то теперь время хода луча будет:

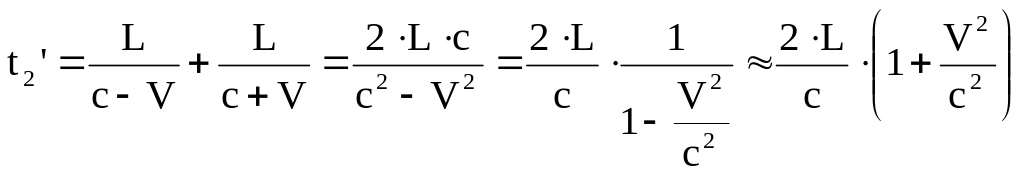
т.к. луч идет к зеркалу со скоростью , а обратно ‑ .

Рассмотрим далее луч .

Р аньше он затрачивал время, как и первый луч:

Теперь, пока луч будет идти от пластинки к зеркалу , это зеркало сместится в положение (см. рис. 1.28), и пока этот луч идет обратно к пластинке , зеркало будет в положении . Следовательно, луч света пройдет путь не , а :

Но , отсюда:

Следовательно, теперь луч затратит время равное:

При этом разность хода лучей и будет равна:

При повороте интерферометра на 90⁰ смещение изменит знак, следовательно, общая разность хода будет равна .

Число полос , на которое сместится интерференционная картина, будет соответственно равно:

В своем опыте Майкельсон использовал интерферометр, с плечом и свет, с длиной волны . При этом число полос, на которое должна сместиться интерференционная картина, должно быть равным

Чувствительность интерферометра Майкельсона порядка 0,01 полосы. Т.е. вполне удовлетворительная точность.

Многочисленные эксперименты на интерферометре Майкельсона, и другие аналогичные, дали отрицательный результат.

Эфирный ветер обнаружить не удалось!

Вывод.

Либо эфир полностью увлекается движущимися материальными телами, что противоречит явлению аберрации звезд, либо частично, но так, что не влияет на аберрацию звезд.

Таким образом, получается следующая картина.

1. Скорость света оказывается постоянной величиной, каким бы способом и в какой бы системе отсчета ее не измеряли.

2. Гипотеза существования эфира не могла объяснить одновременно и аберрацию звезд и отрицательный результат опытов Майкельсона.

Постулаты теории относительности

Отсюда вытекает вывод, что никакого эфира вообще нет.

На этом основании Эйнштейн сформулировал первый постулат специальной теории относительности, или, как говорят, принцип относительности Эйнштейна.

Все законы в природе инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой.

Раньше этот принцип формулировался только по отношению к законам механики.

На основании того факта, что скорость света оказывалась постоянной величиной, был сформулирован второй постулат.

Скорость света в пустоте одинакова во всех инерциальных системах отсчета и не зависит от движения источника и приемника.

Эти два постулата заставляют отказаться от привычных понятий пространства и времени, как от неких абсолютных не связанных друг с другом категорий.

Особенно действующим на воображение является второй постулат. Он, в частности приводит к представлениям о взаимосвязи пространства и времени на таком простейшем примере.

П усть имеются две инерциальные системы отсчета, движущиеся друг

относительно друга со скоростью вдоль осей (см. рис. 1.29).

В некоторый момент времени из точки посылают во все стороны световой сигнал. Свет распространяется с одной и той же скоростью по всем направлениям. Поэтому, неподвижных, относительно системы , точек и , находящихся на одинаковом расстоянии от точки , свет достигнет через одинаковые промежутки времени.

Т.е., два события ‑ достижения светом точек и ‑ в системе совершаются одновременно.

В системе , согласно второму постулату, свет также распространяется по всем направлениям с той же скоростью, что и в системе . Но точки и в системе движутся. Поэтому луч света сначала достигнет точку ‑ она движется ему навстречу, а потом точку ‑ она удаляется от него.

Т.е. то же событие в системе ‑ достижение светом точек и ‑ является неодновременным.

Таким образом, ход времени зависит от системы отсчета.

Преобразования Лоренца

Найдем теперь эти преобразования координат и времени, которые согласуются с постулатами Эйнштейна.

Для этого рассмотрим те же самые системы координат (см. рис. 1.29) и , движущиеся относительно друг друга со скоростью .

Пространство однородно (нет пока экспериментальных фактов, указывающих на неоднородность пространства). Тогда формулы преобразования координат не должны зависеть от переноса начала координат. Этому условию удовлетворяют лишь линейные преобразования.

Далее, плоскость совпадает с плоскостью . Из всего этого следует, что:

Поскольку системы и равноправные, можно записать:

Отсюда следует, что .

Знак плюс соответствует одинаковому направлению осей , а знак минус ‑ противоположному.

Итак

То же и для оси

В механике Галилея было

Отсюда следовало

Но это преобразование скоростей противоречит второму постулату. Действительно, если в системе , то в системе

что не может быть.

Следовательно, преобразования Галилея нужно заменить другими, но тоже линейными (в силу изотропности пространства). Поэтому запишем:

(А)

в силу равноправности систем и . Для нахождения воспользуемся вторым постулатом.

Пусть в момент времени, когда системы были совмещены ‑ , посылают свет, который производит вспышку на экране в точке . Это событие. Его координаты в системе будут:

В системе

Подставим это в уравнения (А) преобразования координат:

Перемножив эти два уравнения, получим:

Отсюда вытекает, что

Для сокращения, обычно пишут

Найдем теперь формулу преобразования времени.

Для этого исключим из системы (А) координату :

Раскроем скобки

Выразим отсюда время

Преобразуем получившееся уравнение

Раскроем теперь

Получили формулу преобразования времени.

Итак, мы получили следующие преобразования координат и времени.

(1.62)

Эти формулы носят название формул преобразования Лоренца, поскольку впервые их записал Лоренц.

При малых скоростях ‑ формулы Лоренца переходят в формулы Галилея.

Одновременность событий в разных системах отсчета

Пусть в системе в точках и в момент времени одновременно происходят два события. Тогда в системе координаты этих событий

1. Если , то и .

2. Если , то и и

Т.е. события, одновременные в системе могут быть не одновременными в системе .

Длительность событий

Пусть в некоторой точке системы происходит событие, длящееся :

В системе

- промежуток времени в системе , т.е. в системе, относительно которой тело (ракета) покоилось. Т.е. в системе координат, связанной с ракетой, т.е. собственное ракетное время.

- промежуток времени в системе , т.е. в системе, относительно которой тело (ракета) движется со скоростью . Т.е. в системе координат, связанной с Землей, т.е. собственное земное время.

Итак, если ракетное время равно 10 лет, то земное . Пусть . Тогда . При .

Длина тел в разных системах отсчета

Пусть в системе покоится стержень, длинной ., которую мы измеряем в один и тот же момент времени

Посмотрим, какова будет его длина относительно системы .

Следовательно

Т.е. аналогичное соотношение имеет место и для линейных размеров.

Если длина тела (ракеты) в системе координат, связанной с телом (ракетой) ‑ , то в системе координат, относительно которой тело движется (Земля) его размеры будут больше. При ‑ . При . Или, наоборот, у движущихся тел размеры в направлении движения сокращаются.

Релятивистское сложение скоростей

Скорость тела в системе определяется как

В штрихованной системе отсчета

Используя связь между найдем.

Отсюда вытекает:

И, аналогично

Если тело движется только вдоль оси

Пусть , тогда

Т.е. вытекает постоянство скорости света в разных системах отсчета.

Эффект Доплера

Пусть в начале координат системы находится излучатель (см. рис. 1.30). В начале координат системы ‑ приемник.

Уравнение колебаний в системе имеет вид:

где знак «‑» берется потому, что волна распространяется в отрицательном направлении оси .

Уравнение колебаний в системе

(В)

Поскольку верен принцип относительности и все законы природы (в частности закон распространения электромагнитных волн) имеют одинаковый вид в любых инерциальных системах отсчета.

Но в системе уравнение колебаний можно получить, исходя из уравнения колебаний в системе , путем замены на и на :

Сравнивая последнее уравнение с уравнением В, получим:

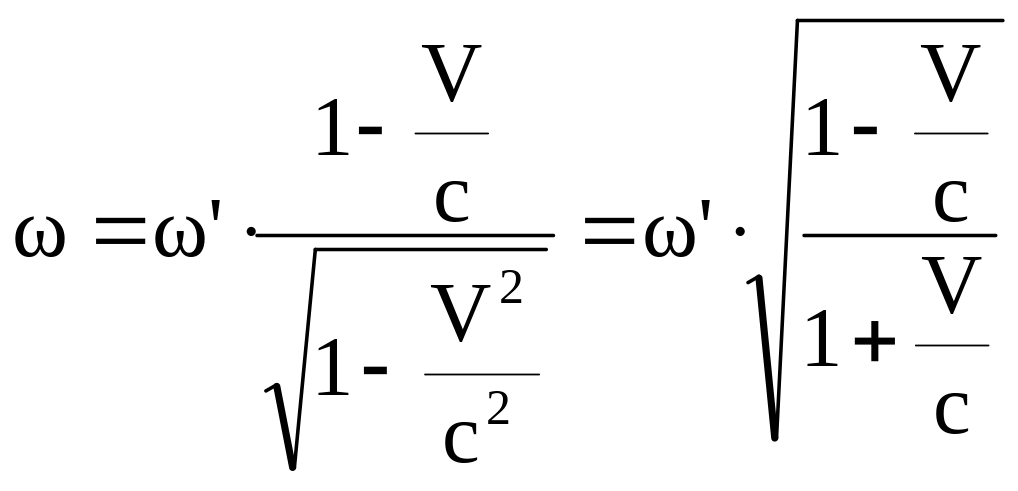
Переходя к линейной частоте, получим:

Или, окончательно, при

(1.63)

Отсюда, относительное изменение частоты:

Это мы будем наблюдать, так называемый продольный эффект. Но кроме того будет наблюдаться и поперечный эффект Доплера, который в акустике не наблюдается. Однако тут формула для изменения частоты другая:

Поперечный эффект Доплера обусловлен изменением течения времени в различных инерциальных системах отсчета.

Эффект Доплера может быть использован для определения радиальной скорости звезд.

Наличием эффекта Доплера объясняется уширение спектральных линий вследствие теплового движения излучающих атомов и молекул.

В частности, с помощью эффекта Доплера были измерены радиальные скорости видимых Галактик. Оказалось, что все Галактики удаляются от нас со скоростью . Причем, чем дальше от нас находится Галактика, тем больше скорость , так, что выполняется соотношение:

Значение этой константы определено эмпирически.

Величину , имеющую размерность времени, называют возрастом Вселенной:

Величину , имеющую размерность длины, называют радиусом Вселенной:

Точный смысл этих величин, однако, до сих пор не ясен.

Понятие о релятивистской динамике

Принцип относительности устанавливает, что все законы природы инвариантны относительно преобразований координат от одной инерциальной системы отсчета к другой.

Однако законы Ньютона не инвариантны относительно преобразований Лоренца. Так, второй закон Ньютона в системе имеет вид:

Аналогичный вид он должен иметь и в системе :

Попробуем получить это с помощью преобразований Лоренца:

Отсюда следует, что при преобразованиях координат должна преобразовываться и масса тела. Закон преобразования массы имеет вид:

Необходимо отметить, что при этом преобразуются и силы, но это выходит за рамки нашего курса.

В этом случае, выражение для импульса материальной точки будет иметь вид:

При этом инвариантная форма записи второго закона Ньютона имеет вид:

Найдем релятивистское выражение для энергии. Для этого левую и правую части инвариантной формы второго закона Ньютона умножим на величину :

Но выражение , т.е. работа, совершенная над телом за время . Работа должна быть равна изменению энергии:

Вспомним, что . С учетом этого, выражение для изменения энергии примет вид:

Произведя дальнейшие преобразования, получим:

(1.64)

Либо:

В этом случае кинетическая энергия тела будет равна:

При малых скоростях, , выражение для кинетической энергии примет вид:

Т.е. при малых скоростях получили привычное выражение для кинетической энергии.

Получим теперь выражение для полной энергии через импульс. Итак, . Возведем это выражение в квадрат:

Аналогично, возведем в квадрат выражение для импульса:

Подставим сюда полученное выражение для квадрата скорости :

Преобразовывая далее, получим:

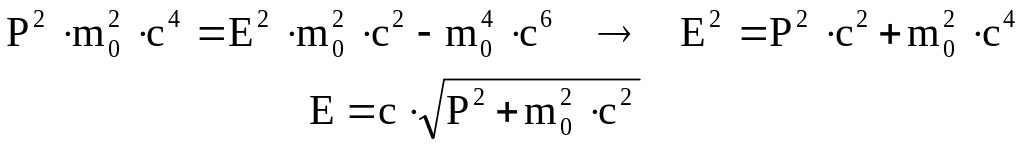(1.65)

«Черные дыры»

Выше мы получили выражение для гравитационной потенциальной энергии (1.47). Но, как известно, тела взаимодействуют посредством полей. В частности, гравитационное взаимодействие осуществляется посредством гравитационного поля. Следовательно, гравитационное поле должно обладать энергией.

Т.е. если существует тело массы , то вокруг него имеется гравитационное поле, обладающее определенной энергией. Расчеты показывают, что величина этой энергии:

где ‑ масса шарообразного тела, ‑ радиус этого тела.

Эту энергию необходимо понимать как необходимую величину энергии, нужную для того, чтобы тело распылить на мельчайшие частицы, находящиеся на расстояниях, при которых их энергия взаимодействия будет равна нулю.

Сравним эту гравитационную энергию с энергией покоя, например, для Земли. Для этого приравняем эти энергии и из получившегося уравнения найдем радиус Земли, при котором ее энергия покоя равна гравитационной энергии ‑ так называемый гравитационный радиус.

Здесь ‑ масса Земли, ‑ гравитационная постоянная, ‑ скорость света.

В то время как радиус Земли равен . Аналогичные расчеты для Солнца дают величину , в то время как радиус Солнца равен .

Таким образом, гравитационная энергия имеет пренебрежимо малую роль в общем энергетическом балансе макроскопических тел.

Посмотрим, как обстоит дело для видимой части Вселенной. Оценки плотности вещества Вселенной дают такую величину , т.е. порядка 100 протонов на 1 м³. Тогда массу всей вселенной можно оценить как , и ее гравитационную энергию как , где ‑ радиус Вселенной. Приравнивая энергию покоя вселенной ее гравитационной энергии, найдем ‑ гравитационный радиус Вселенной.

Подставив числовые значения, получим: , что совпадает с наблюдаемым радиусом Вселенной.

Расчеты показывают, что если тело данной массы имеет размеры своего гравитационного радиуса, то никакие сигналы выйти за пределы этого гравитационного радиуса не могут. В частности и свет.

Если какие либо тела или лучи будут проходить мимо, то они будут втягиваться внутрь гравитационного радиуса и там бесследно исчезать.

Наружу будет выходить лишь гравитационное поле чудовищной величины. Так, например, для Земли:

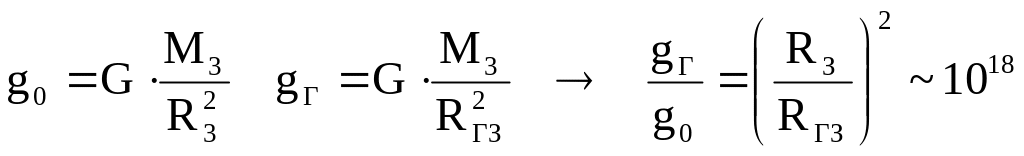
Таким образом, для внешнего наблюдателя эта область будет казаться Черной дырой.

С этой точки зрения, вся наша Вселенная ‑ Черная дыра для постороннего наблюдателя. Никакие процессы, сигналы не могут выйти за пределы нашей Вселенной.

Лекция 7 (2 часа)

Собственные колебания..

(Колебательное движение. Классификация колебаний. Сво­бодные колебания. Собственные колебания на примере пружинного, математического и физического маятников. Гармонические колебания. Дифференциаль­ное уравнение гармонических колебаний, его решение. Гармонический осцилятор. Энергия гармонического осциллятора)

.