Уравнения плоских кривых

Уравнение явного вида Y=f(X), где f(X) - заданная функция от X, является удовле-творительным

в том случае, когда функция однозначна, а кривая не имеет вертикальных касательных.

Неявное уравнение X*X+Y*Y-r*r=0 применяется для окружности. Неявное уравнение в общем

случае записывается в виде f(X,Y)=0, где f(X,Y) - функция от X и Y.

Наиболее распространенными неявными уравнениями являются уравнения кониче-ских сечений.

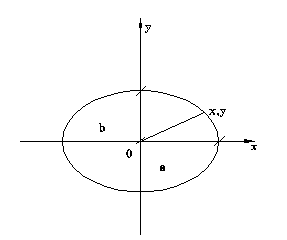
Уравнение для эллипса

Уравнение для параболы Y*Y-4aX=0.

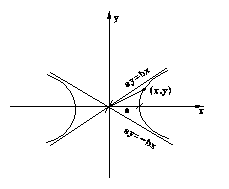
Уравнение для гиперболы

В общий случае, все типы конических сечений описываются уравнением второй сте-пени:

S=aX*X+2hXY+bY*Y+2gX+2fY+c=0, где a,b,c,f,g,h – различные между собой коэффициенты.

Если выполняется соотношение h*h<2, то кривая принимает вид эллипса; если h*h=ab, то

вид параболы; если h*h>ab, то гиперболы, при условии, что abc+2fgh-2fgh-af*f-bg*g-ch=/0

Параметрические уравнения прямых и кривых

В случае, когда много вертикальных касательных использование вышеперечисленных уравнений

затруднительно и они непригодны для генерирования кривых. Существует еще один способ

описания, при котором равноправные координаты X и Y - уравнения параметрического вида;

X и Y функции от некоторого параметра t, X=X(t), Y=Y(t).

Пример: Окружность X2+Y2=1 в параметрическом виде записывается X=cos(t) , Y=sin(t),

0 <=t<=2п При условии 2п/3<=t<=7п/6 дает полное описание дуги ABC окружности.

Если X(t) и Y(t) - линейные функции от t, то рассматриваемая кривая будет прямой. В частности

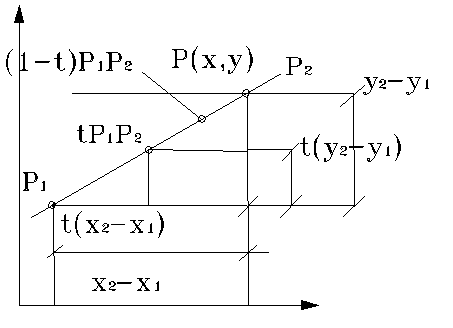
прямая проходящая через Р1 и Р2 определяется по формулам,

X=X1+t(X2-X1), Y=Y1+t(Y2-Y1).

Точка P(X,Y) , как показано на рисунке делит прямую, соединяющую точки Р1 и Р2, на

отрезки в отношении t:(1-t). Для доказательства используется подобие треугольников.

Прямая aX+bY+c=0 описывается параметрическим уравнением :

Касательная к кривой X=X(t), Y=Y(t) в точке Р с параметром t=t1 определяется уравнением

X=X(k)=X(t1)+kX(t1), Y=Y(k)=Y(t1)+kY(t1) , где k- параметр на касательной, а X(t1) и Y(t1)

значение производных dX/dt и dY/dt в точке t=t1.

Нормаль в данной точке кривой определяется по формулам X=X(t1)+kX(t1), Y=Y(t1)-kY(t1).

Кривизна

Радиус кривизны R кривой Y=Y(X) определяется известной формулой

Так как R бесконечен в точках перегиба кривой, удобнее

пользоваться самой кривизной H=1/R,

поскольку это величина конечная, если нет заострений на кривой:

Соответствующая формула в параметрическом виде кривой X=X(t), Y=Y(t).

В неявном виде f(X;Y)=0

Вывод последних двух формул рекомендуется выполнить самостоятельно.

Трехмерные интерактивные графические методы

Трехмерные интерактивные графические методы предназначены для графического ввода и

моделирования трехмерных объектов в процессе диалога человека с ЭВМ. Они в основном

имеют аналоги двухмерных методов интерактивного ввода. Трехмерные интерактивные

графические методы являются рабочим инструментом для выполнения графических построений

с целью моделирования непосредственно на перспективных и аксонометрических изображениях,

а также в ортогональных проекциях.

Трехмерное позиционирование - метод графического задания точки в модели пространства,

наглядные изображения или ортогональные проекции которого воспроизводятся на экране

дисплея. Основная цель - формирование 3D объектов и размещение их в пространстве.

Различаются следующие виды трехмерного позиционирования: в пространстве, на плоскостях

пространства, на поверхностях.

Позиционирование в пространстве - графическое задание точки в моделируемом пространстве

вне поверхностей объектов и получение ее трехмерных координат. Основной способ –

использование УПС (управляемого пространственного символа, локатора).

Позиционирование на плоскостях пространства - метод предназначен для задания точки в

пространстве, указанием ее на наглядном изображении или ортогональной проекции отсека

плоскости, которой должна принадлежать точка. Для определения трехмерных координат

этой точки решается задача на пересечение проецирующего луча, соответствующего

указанной точки, с данной плоскостью.