2. Записать в троичной системе счисления число 58

Билет №4

1. Древнеегипетская система счисления.

Примерно в третьем тысячелетии до нашей эры древние египтяне придумали свою числовую систему, в которой для обозначения ключевых чисел 1, 10, 100 и т.д. использовались специальные значки — иероглифы.Все остальные числа составлялись из этих ключевых при помощи операции сложения. Система счисления Древнего Египта является десятичной, но непозиционной и аддитивной.

	1. Как и большинство людей для счета небольшого количества предметов Египтяне использовали палочки.
	Если палочек нужно изобразить несколько, то их изображали в два ряда, причем в нижнем ряду должно быть столько же палочек, сколько и в верхнем, или на одну больше.
	10. Такими путами египтяне связывали коров
	Если нужно изобразить несколько десятков, то иероглиф повторяли нужное количество раз. Тоже самое относится и к остальным иероглифам.
	100. Это мерная веревка, которой измеряли земельные участки после разлива Нила.
	1 000. Вы когда-нибудь видели цветущий лотос? Если нет, то вам никогда не понять, почему Египтяне присвоили такое значение изображению этого цветка.
	10 000. "В больших числах будь внимателен!" - говорит поднятый вверх указательный палец.
	100 000. Это головастик. Обычный лягушачий головастик.
	1 000 000. Увидев такое число, обычный человек очень удивится и возденет руки к небу. Это и изображает этот иероглиф
	10 000 000. Египтяне поклонялись Амону Ра, богу Солнца, и, наверное, поэтому самое большое свое число они изобразили в виде восходящего солнца

2. Записывались цифры числа начиная с больших значений и заканчивая меньшими. Если десятков, единиц, или какого-то другого разряда не было, то переходили к следующему разряду.

3. - 1205, - 1 023 029

4. Попробуйте сложить эти два числа, зная, что более 9 одинаковых иероглифов использовать нельзя, и вы сразу поймете, что для работы с этой системой нужен специальный человек. Обычному человеку это не под силу.

2. В троичной системе записано число . Переписать это же число в двоичной системе.

Билет №5

1. Древнейшая позиционная система – вавилонская.

2. Вавилонская десятеричная / шестидесятеричная

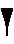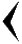3. В древнем Вавилоне примерно во II тысячелетие до нашей эры была такая система счисления - числа менее 60 обозначались с помощью двух знаков: для единицы, и для десятка. Они имели клинообразный вид, так как вавилоняне писали на глиняных табличках палочками треугольной формы. Эти знаки повторялись нужное число раз, например

4. - 3; - 20; - 32; - 59

5. Числа больше 60 записывались по разрядам, с небольшими пробелами между ними:

6. Так записывается число 302, то есть 5*60+2.

   1*60*60+2*60+5 = 3725

7. А это 1*60*60+2*60+5 = 3725.

8. Но представление не которых чисел в этой системе будет одинаковым, например, число 302, может быть и равно и 5*60*60 + 2 = 18002. Так как нет значка для обозначения нуля.

9. Лишь в V веке до нашей эры был введен особый знак 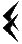- наклонный клин для обозначения пропущенных разрядов, игравший роль нуля.

   2*60*60+3 = 7203

10. это запись числа 7203 (2*60*60+3).

11. Однако отсутствие низшего разряда не обозначалось, и поэтому число 180 = 3*60 записывалось так , а обозначать эта запись могла и 3, и 180, и 10800 (3*60*60), и т. д.

12. Считается, что десятичная система была у шумеров, а после того как их завоевали семиты, их система была приспособлена под шестидесятеричную систему семитов.

13. Шестидесятеричная запись целых чисел не получила широкого распространения за пределами Ассиро-вавилонского царства, но шестидесятеричные дроби применяются до сих пор при измерении времени. Например, одна минута = 60 секунд, один час = 60 минут.