27.Точечные и интервальные оценки. Точность оценки, доверительная вероятность(надежность).Доверительный интервал.

Точечные оценкиСтатистической оценкойнеизвестного параметра случайной величины

X называется функция вариант x1 , x2 , …, xi, …, xn.

Несмещенной называют статистическую оценку, математическоеожидание которого равно оцениваемому параметру при любом объеме

выборки.Смещеннойназывают статистическую оценку, математическое ожиданиекоторой не равно оцениваемому параметру.Выборочной средней(оценкой математическогоожидания) называют

среднее арифметическое наблюдаемых значений количественного признака =

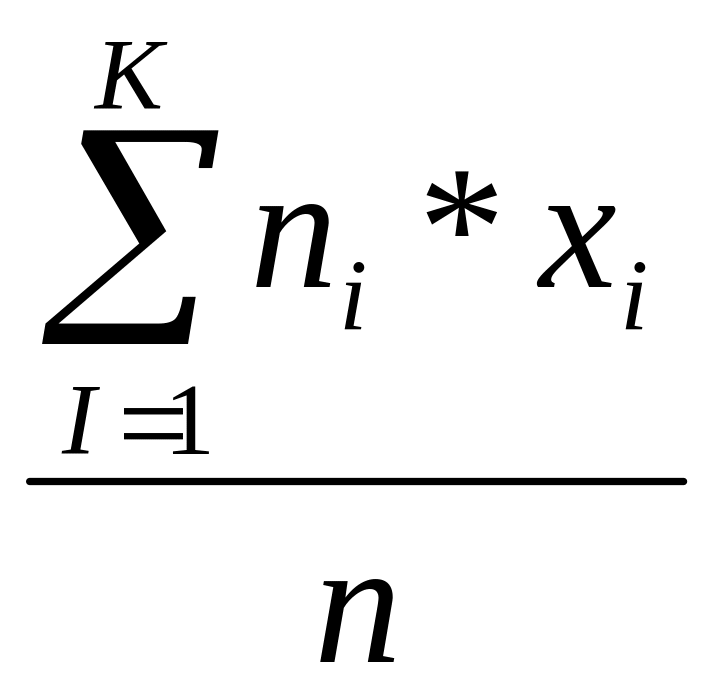
xi— варианта выборки,

ni— частота варианты, — объем выборки,

k — число наблюдаемых различных значений случайного параметра X .

Таким образом, выборочная средняяесть средняя взвешенная значенийпризнака с весами, равными соответствующим частотам.Допустим, что все наблюдаемые значения количественного признака

(случайной величины) X выборки разбиты на несколько групп.Рассматривая каждую группу как самостоятельную, можно найти ее

среднюю арифметическую.Групповой среднейназывают среднее арифметическое значений признака,

принадлежащих группе.Зная групповые средние и объемы группы, можно найти общую

среднюю: общая средняя равна средней арифметической групповых средних,взвешенной по объемам групп.Для того, чтобы охарактеризовать рассеяние значений количественногопризнака X совокупности вокруг своего среднего значения xв, вводят

характеристику — выборочную дисперсию.

Выборочной дисперсиейназывают среднее арифметическое квадратов

отклонений наблюдаемых значений количественного признака X от

выборочного среднего xв: =

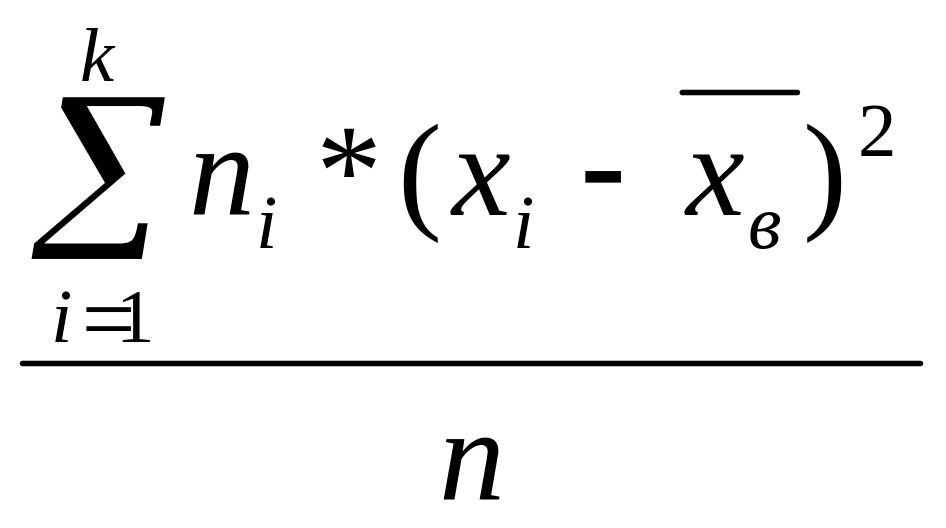
то есть выборочная дисперсия есть средняя взвешенная квадратовотклонений с весами, равными соответствующим частотам.Кроме выборочной дисперсии для характеристики рассеяния значений

количественного признака X вокруг своего выборочного среднего значенияпользуются характеристикой — выборочным средним квадратическим

отклонением.Выборочным средним квадратическим отклонениемвыборочным

стандартом) называют квадратный корень из выборочной дисперсии:σ в = .

Вычисление дисперсии можно упростить, используя формулу:Dв= .

Выборочная дисперсия Dвявляется смещенной оценкой дисперсии. Для

того, чтобы получить несмещенную оценку дисперсии, нужно "исправить"

величину Dв.

Исправленной выборочной дисперсией S² называется величина: =

Исправленным выборочным средним квадратическим отклонениемназывается величина:

S = .

Все рассмотренные выше статистические оценки называются точечными,так как они определяются одним числом.

Интервальные оценкиИнтервальнойназывают оценку, которая определяется двумя

числами — концами интервала, покрывающего оцениваемый параметр.

Доверительнымназывают интервал длиной 2δ , который с заданной

вероятностью (надежностью) γ покрывает оцениваемый параметр. Величина

δ , равна половине доверительного интервала, называется точностью

оценки.

29. Статистические гипотезы. Нулевая и конкурирующая гипотезы. Ошибки 1-го и 2-го рода. Стат. Критерий проверки нулевой гипотезы.

Статистической называют гипотезу о виде неизвестного распределения, или о параметрах известных распределений. Наряду с выдвинутой гипотезой рассматривают и противоречащую ей гипотезу. Если выдвинутая гипотеза будет отвергнута, то имеет место противоречащая гипотеза. Нулевой (основной) называют выдвинутую гипотезу Н₀.Конкурирующей (альтернативной) называют гипотезу Н₁, которая противоречит нулевой.

Выдвинутая гипотеза может быть правильной и неправильной, поэтому возникает необходимость ее проверки. Поскольку проверку производят статистическими методами, ее называют статистической. В итоге статистической проверки гипотезы в двух случаях может быть принято неправильное решение, т.е. могут быть допущены ошибки 2-х родов. Ошибка 1-го рода состоит в том, что будет отвергнута правильная гипотеза. Ошибка 2-го рода состоит в том, что будет принята неправильная гипотеза. Вероятность совершить ошибку 1-го рода называется уровнем значимости и обозначается α. На практике обычно равна 0,05 или 0,01.

Стат. критерий – СВ-на К, которая служит для проверки нулевой гипотезы.

Наблюдаемым значением называют значение стат. критерия, вычисленное по данным выборки. Критической областью называют совокупность значений критерия К, при которых нулевую гипотезу отвергают. Областью принятия гипотезы называют совокупность значений критерия К, при которых гипотезу принимают. Критическими точками называют точки, отделяющие критическую область от области принятия гипотезы. Критические области бывают правосторонние и левосторонние.

Принцип проверки стат. гипотезы: если К_набл принадлежит критич. области, то нулевую гипотезу отвергают; если К_набл принадлежитобласти принятия гипотезы, то нет оснований отвергать нулевую гипотезу. Для каждого критерия имеются спец. таблицы, по которым находятся критич. точки для заданного уровня значимости α.

30.Критической областью наз.сов-ть знач.критерия,при кот-х нулевую гипотезу отвергают.Областью принятия гипотезы наз.сов-ть знач. критерия,при кот-х гипотезу принимают.Критическими точками наз.точки,отделяющие критическую область от области принятия гипотезы.Различают одностороннюю и двустор. критич.области.Правостор.наз.критич.область,определяемую нерав-ом К›к_кр,где к_кр-полож.число.Левостор.наз.критич.область,опред-уюнер-ом К‹к_кр,гдек_кр-отриц.число.Одностор.наз.правостор.илилевостор.критич.область.Двустороннейназ.критич.областьопред.нер-ми К‹к₁,К›к₂,где к₂›к₁.Для отыскания правостор.критич.области достаточно найти критич.точку.Для её нахождения задаются достаточной малой вероятностью-уровнем значимости α.Затем ищут критич.точку,исходя из требования,чтобы при усл.справедливости нулевой гипотезы вероятность того,что критерий примет значение,большеек_кр,была равна: Р(К›к_кр)=α.Левостор.критич.областьопр-сянер-ом К‹к_кр(к_кр‹0).Критич.точкунаходят исходя из требования,чтобы при справедливости нулевой гипотезы вероятность того,что критерий примет знач.,меньшеек_кр,была равна Р(К‹к_кр)=α. Двустор.критич.обл.опр.нер-ми К‹к₁,К‹к₂.Критич.точки нах-т из трбования,чтобы при справедл-ти нулевой гипотезы сумма вер-тейтого,что критерий примет знач.,меньшее к₁ или большее к_2, была равна: Р(К‹к₁)+Р(К›к₂)=α. Мощностью наз.вер-ть попадания критерия в критич. обл. приусл. ,что справедлива конкурирующая гипотеза.

33. Коэффициент корреляции rxyСВX,Yназ-т отношение корреляционного момента к произведению средних квадратических отклонений этих величин

34. Метод нахождения оценки 0 неизвестного параметра в, основанный на минимизации суммы квадратов отклонений выборочных данных от определяемой (искомой) оценки θ. называется методом наименьших квадратов (коротко: МНК).Другими слонами, в МНК требуется найти такое значение θ, кото­рое минимизировало бы сумму F(θ)= МНК является наиболее простым методом нахождения оценок параметра θ.