16. Распределение Пуассона. Примеры.

Пусть производится n независимых испытаний, в каждом из которых вероятность появления событияА равна p. Для определения вероятности k появлений события в этих испытаниях используют формулу Бернулли. Если же n велико, то пользуются асимптотической формулой Лапласа. Однако, эта формула непригодна, если вероятность события мала (p ≤0,1). В этих случаях (n велико, p мало) прибегают к асимптотической формуле Пуассона.

Требуется найти вероятность того, что при очень большом числе испытаний, в каждом из которых очень большом числе испытаний, в каждом из которых вероятность события очень мала, событие наступит ровно k раз.

Допустим, произведение np сохраняет постоянное значение, а именно np = λ. Это означает, что среднее число появлений события в различных сериях испытаний, при различных значениях n, остается неизменным.

Воспользуемся формулой Бернулли для вычисления интересующей нас вероятности:

.

Так как , то . Следовательно,

.

Приняв во внимание, что n имеет очень большое значение, вместо найдем . При этом будет найдено лишь приближенное значение отыскиваемой вероятности: n хотя и велико, но конечно, а при отыскивании предела мы устремим n к бесконечности. Итак,

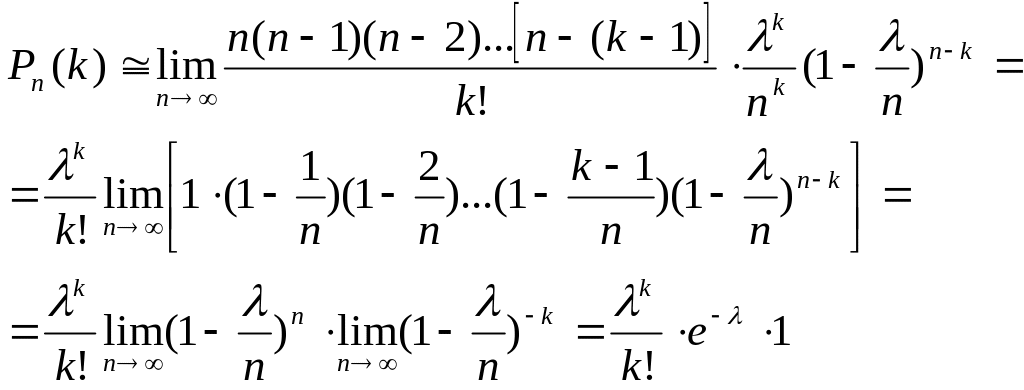
Итак (для простоты записи знак приближенного равенства опущен),

.

Эта формула выражает закон распределения Пуассона вероятностей массовых (n велико) редких (p мало) событий.

Пример. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,0002. Найти вероятность того, что на базу прибудут 3 негодных изделия.

Решение. По условию n =5000, p =0,0002, k =3. Найдем λ:

λ= np=5000·0,0002=1.

Искомая вероятность по формуле Пуассона приближенно равна

.

17. Показательным(экспоненц-ным) назыв. Распределение вероятностей непрерывн. СВ, заданное формулой: λ>0 const

- Ф-ция показательного распределения

Момент времени наступления некот. События в простом потоке событий, т.е. непрер. СВ с показат. Распределением.

M(x)=∫ от 0 до + ∞ (xde^–λx)dx = 1/λ

D(x)=∫ от 0 до + ∞ ((1-1/x)^2 * λe^–dx)dx=1/ λ^2

δ(x)=корень из D(x)=1/ λ

Назовем элемент устройством. Элем нач. работать в момент врем. T0, а по истеч. врем. Длит-тьюt происходит поломка. F(t)=P(T<t) вер-ть безотказной работы за время t=P(t)=p(T>=t)=1-F(t) – ф-ция надежности.

Непрерывная с. в. Х имеет равномерное распределение на отрезке |а,в], если ее плотность вероятности f(x) постоянна на этом отрезке, а вне его равна пулю:

отсюда следует, что вместо отрезка \а,Ь) можно

писать [а.b) или (а, в), [в,в). так как с.в. Х — непрерывна.

19..Правило «3 сигм.Правило «3 сигм»:Если случайная величина распределена нормально,то абсолютная величина ее отклонения от мат.ожидания не превосходит утроенной σ.

На практике поступают так: Если распределение изучаемой СВ неизвестно,то правило «3 сигм» выполнено,то есть все основания считать,что изучаемые СВ распределенынормально.В противном случае-не нормально.

20. Если каждому возможному значению с. н. Х по определенному пра­вилу соответствует одно возможное значение с. в. У, то У называют функцией случайного аргумента X, записывают У = φ{X).

Пусть X — д.с.в. с возможными значениями x1.x2,х3,...,хn„, ве­роятности которых равны соответственно p1.p2,p3,...,pn, т.е. рi = Р{Х →←xi), i = 1,2,3,-.-,п. Очевидно, что св. У = φ{X).так­же д.с.в. с возможными значениями y1 = φ{x1), y2 = φ{x2), y3 = φ{x3)…… yn = φ{xn)вероятности которых равны соответственно Р1,Р2,Рз,..-,Рп. т.е. если yi = φ{xi), то р= Р{У = уi) = Р{Х =xi}, i = 1,п.

Отметим, что различным значениям св. X могут соответствовать одинаковые значения с и. Y. В этом случае вероятности повторяющих­ся значений следует складывать.

Математическое ожидание и дисперсия функции У = φ{X).опреде­ляются соответственно равенствами

Для решения ряда практических задач необходимо знать закон рас­пределения (или числовые характеристики) случайных величин вида Z = X±Y,Z = XY,Z = +, Z =mах(х, У) и других.

21. Если каждой паре возможных значений св. X и У по определен­ному правилу соответствует одно возможное значение с. в. Z, то Z называют функцией двух случайных аргументов X и Y, записывают Z = φ(X.У). Найдем закон распределений суммы двух случайных величин (наи­более важный па практике), т. о. закон распределения с. в. Z = X + У.Пусть система двух непрерывных св. (Х,У) имеет совместную плотность распределения f(х,у). Найдем по формуле функцию распределения cв. Z = X + У.

Fz(z) = P{Z < z} = Р[Х + Y<z) =

Здесь D, множество точек плоскости Оxу, координаты которых удо­влетворяют нераввнству х + у <z ,

Имеем

Дифференцируя полученное равенство по переменной т. входящей в верхний предел внутреннего интеграла, получаем выражение для плот­ности распределения с. в. Z =Х + У:

fz(z)=

Закон распределения суммы независимых с. е. называется компо­зицией или сверткой законов распределения слагаемых

22.Упорядоченный набор (X1,Х2,....Хn) случайных величин Xi (i = 1,n), заданных на одном и том же ПЭС Ω. называется п-мерной с-лучайной величиной или системой n случайных величин.Одномерные с. в. X1,Х2,....Хn называются компонентами или её ставляющими n-мерной св. (X1,Х2,....Хn ). Их удобно рассма­тривать как координаты случайной точки или случайного вектора X = (X1,Х2,....Хn ) в пространстве n измерений.На многомерные случайные величины распространяются почти без изменений основные понятия и определения, относящиеся к одномер­ным случайным величинам. Ограничимся для простоты рассмотрени­ем системы двух случайных величии; основные понятия обобщаются на случай большего числа компонент.Упорядоченная пара (X, У) двух случайных величин Х и У назы­вается двумерной случайной величиной или системой двух одномерных случайных величин X и У.Систему [X, У) можно изобразить случайной точкой М{Х, Y) или случайным вектором ОМ.

Система (Х,У) есть функция элементарного события: (Х,У) = φ(w). Каждому элементарному событию w ставится в соответствие два действительных числа х и у (или x1 и x2) — значения X Y {или Х1\ и X2) в данном опыте.

. Двухмерная функция распределения двухмерной случайной величины

(Х, Y) равна вероятности совместного выполнения двух событий {Х <х} и

{Y <у}:

F(x,y)=p({X<x}⋅{Y<y}).

Закон распределения дискретной двумерной СВ наз. Соответствие возможных знач. Этой СВ и их вер-ти.

Свойства двухмерной плотности:

1

2 ,

3

4

5 неубывающая функция по каждому из своих аргументов при фиксированном другом аргументе.

24.Математическая статистика раздел математики, в котором изучаются методы сбора, систематизации и обработки результатов на­блюдений массовых Случайных явлений для выявления существующих закономерностей.

Математическая статистика тесно связана с теорией вероятностей. Обе эти математические дисциплины изучают массовые случайные явления. Связующим звеном между ними являются предельные теоре­мы теории вероятностей. При этом теория вероятностей выводит из ма­тематической модели свойства реального процесса, а математическая статистика устанавливает свойства математической модели, исходя из данных наблюдений Предметом математической статистики является изучение случай­ных величин (или случайных событий, процессов) по результатам на­блюдений. Полученные в результате наблюдении (опыта, эксперимен­та) данные сначала надо каким-либо образом обработать: упорядочить, представить в удобном для обозрения и анализа виде . Это первая зада­ча. Затем, это уже вторая задача, оценить, хотя бы приблизительно, интересующие нас характеристики наблюдаемой случайной величи­ны. Например, дать оценку неизвестной вероятности события, оценку неизвестной функции распределения, оценку математического ожида­ния, оценку дисперсии случайной величины, оценку параметров рас­пределения, вид которого неизвестен, и т.д.

Следующей, назовем се условно третьей, задачей является провер­ка статистических гипотез, т. е. решение вопроса согласования ре­зультатов оценивания с опытными данными. Например, выдвигается гипотеза, что: а) наблюдаемая с. в. подчиняется нормальному закону; б) м.о. наблюдаемой с. в равно нулю; в) случайное событие обладает данной вероятностью и т.д.

Одной из важнейших задач математической статистики является разработка методов, позволяющих по результатам обследовании вы­борки (т.е. части исследуемой совокупности объектов) делать обосно­ванные выводы о распределении признака (с. в. -V) изучаемых объектом по всей совокупности.

25.Статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин.

Несмещенной называют статистическую ошибку Q^*, математическое ожидание которой равно оцениваемому параметру Q при любом объеме выборки, т.е. М (Q^*)=Q. Смещенной называют оценку, математическое ожидание которой не равно оцениваемому параметру.

Эффективной называют статистическую оценку, которая (при заданном объеме выборки n) имеет наименьшую возможную дисперсию. При рассмотрении выборок большого объема (n велико!) к статистическим оценкам предъявляется требование состоятельности.

Состоятельной называют статистическую оценку, которая при n → ∞ стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценкипри n → ∞ стремится кнулю, то такая оценка оказывается и состоятельной.