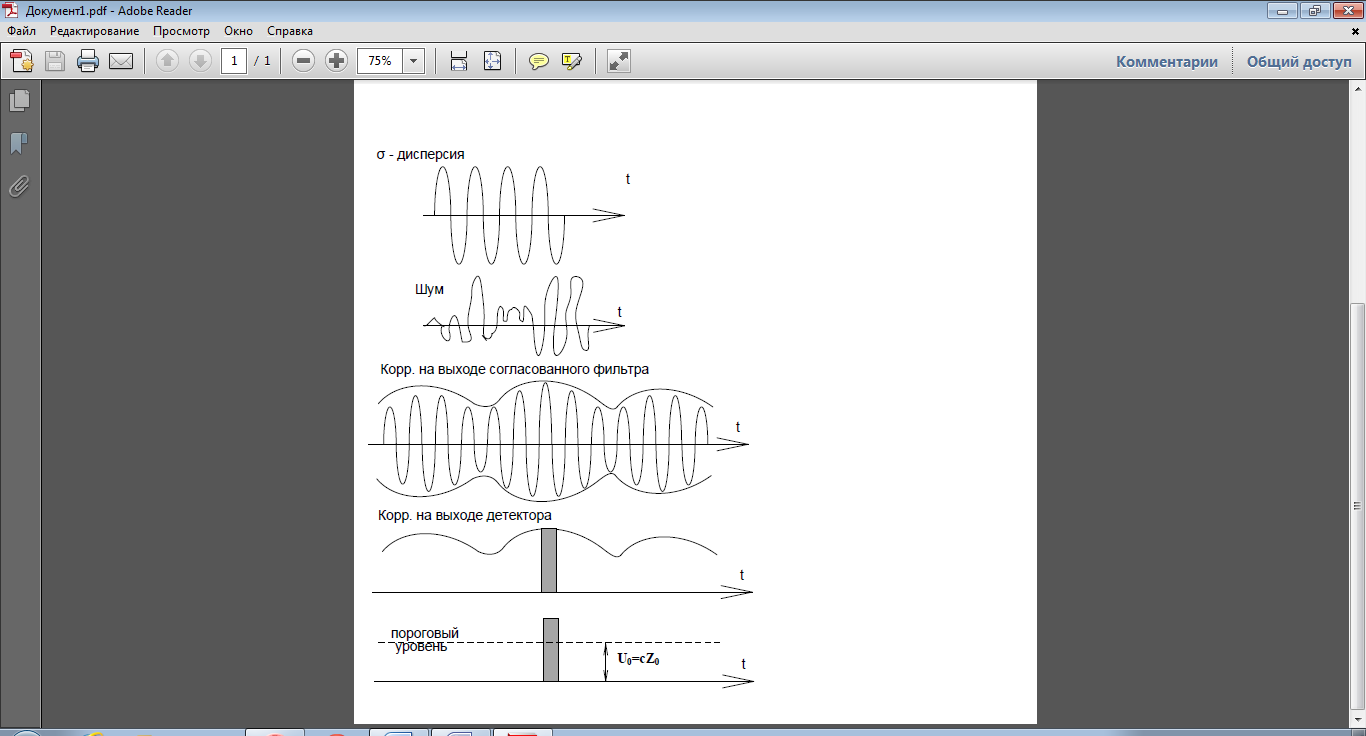
Оптимальная фильтрация.

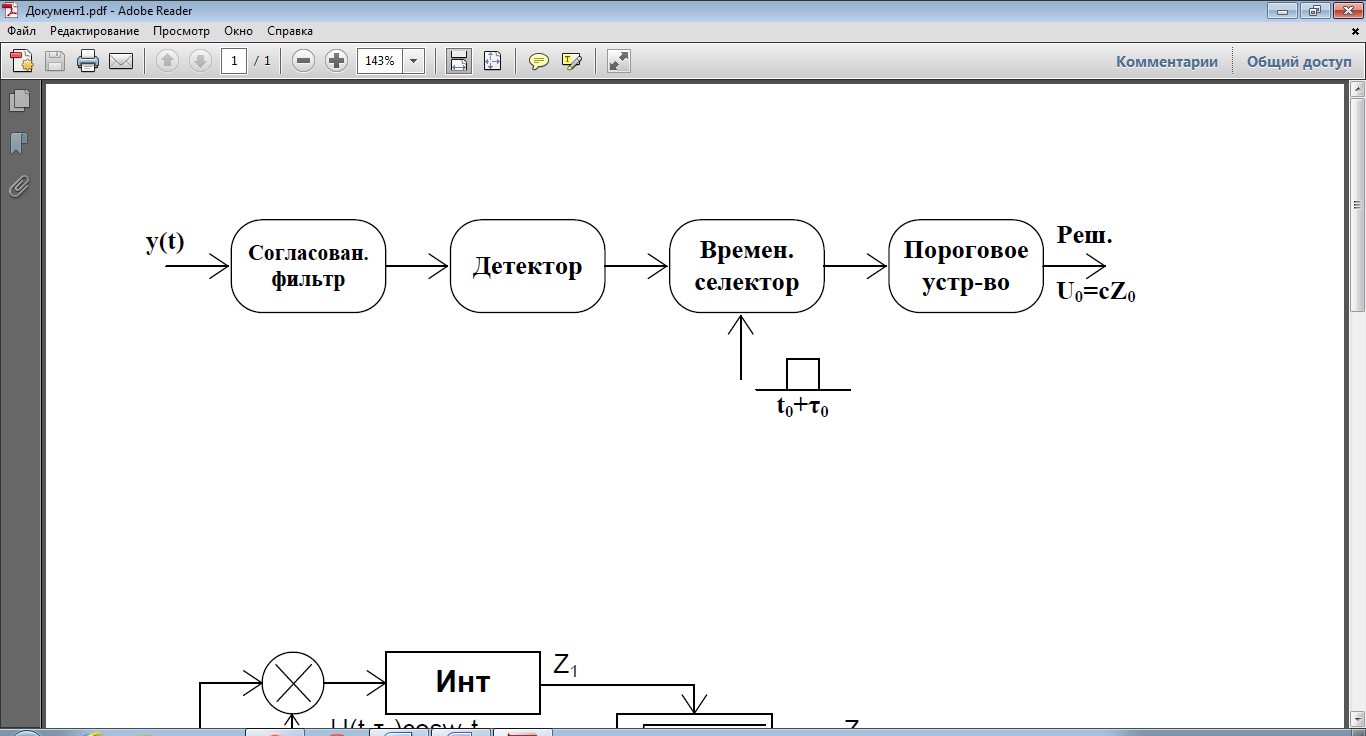
Оптимальный приемник обнаружения с сигналом со случайной начальной фазой (фаза распространяется равномерно [0,2π]) построен с помощью согласованного фильтра. Т.к. при равномерном распределении фазы информация о наличии сигнала содержится только в амплитуде сигнала, то после согласованной фильтрации необходимо продетектировать сигнал (он выделяет огибающую сигнала). В результате детектирование в момент времени τ₀+t₀ совпадает до постоянного множителя с с величиной z (корреляционный интеграл).

Z₀ – тот же уровень порога, который был в предыдущем случае.

Т. о., структура оптимального приемника обнаружения согласованный фильтром содержит СФ, Д огибающей, ВС, ПУ.

Применение СФ позволяет обойтись одноканальной семой обработки сигнала, позволяет обойтись без устройства перемножения, который сложно реализуется.

Качественные показатели оптимального приемника обнаружения.

Напряжение на выходе СФ представляет собой аддитивную смесь полезного сигнала и шума. Огибающая этого напряжения в момент времени τ₀+t₀ подчиняется обобщенному закону распределения Релея.

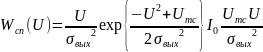– нормальный закон распределения (при наличии сигнала),

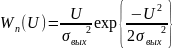– только помехи.

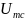– амплитуда сигнала на выходе согласованного фильтра .

Введем обозначения

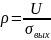
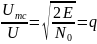- параметр обнаружения

, ,

, ,

.

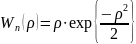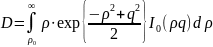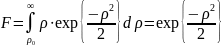Семейство характеристик обнаружения D(q)

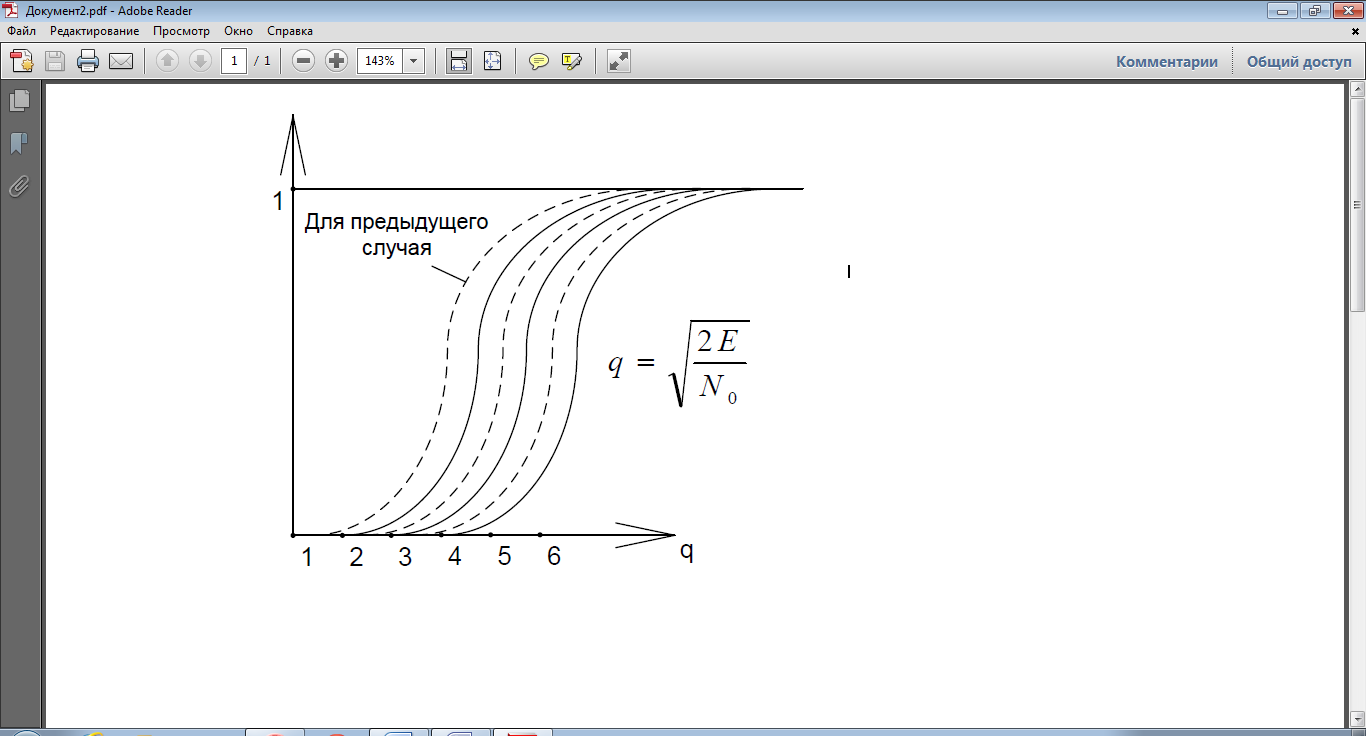
Для сравнения приведения приведены хар-ки обнаружения для сигнала с полностью известными пар-ми (штриховые линии). Сравнение кривых показывает, что незнание начальной фазы сигнала приводит к ухудшению качественных показателей приемника обнаружения.

Пример. Вероятность правильного обнаружения при q=5 равна 0,95, а при неизвестной начальной фазе 0,9. Это различие усиливается с уменьшением отношения энергии сигнала и спектральной плотности шума. В случае сильных сигналов (q>10) качественные показатели рассмотренных приемников почти совпадают.

Тема №7: Сигнал со случайной амплитудой и начальной фазой.

,

,

.

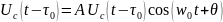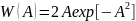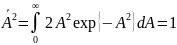Применительно к РЛСигналу, отраженному от движущейся цели А можно считать распределенным по з-ну Релея со средним квадратом =1. Начальную фазу будем полагать независимой от А и определенной на интервале от 0 до 2π.

Запишем отношение правдоподобия для сигнала со случайной начальной фазой:

.

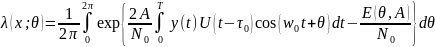Усредняем отношение правдоподобия по всем значениям А:

,

Е- энергия радиоимпульса, A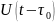 – огибающая этой энергии.

Так как энергия практически не зависит от начальной фазы, то можем записать:

Если А подчиняется закону распределения Релея, то средняя энергия сигнала определяется:

,

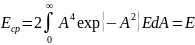Отношение правдоподобия примет вид:

.

Выражение в квадратных скобках- модифицированная функция Бесселя первого рода нулевого порядка:

.

Этот интеграл табличный, его можно записать в следующем виде:

.

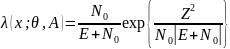Выражение определяет отношение правдоподобия для сигнала со случайной амплитудой и начальной фазой. Интеграл будем рассматривать так же как и в предыдущем случае, сравнивая эти 2 выражения (отношение правдоподобия для сигнала со случайной фазой и со случайной амплитудой и фазой) получаем, что эти выражения являются монотонной функцией Z. Поэтому способы реализации оптимального приемника обнаружения сигнала остаются теми же, которые мы рассматривали ранее. Отличия лишь в качественных показателях этих приемников.