Качественные показатели приемника обнаружения.

Вне зависимости от способа реализации оптимального приемника, процесс обнаружения заключается в сравнении корр-го интеграла с пороговым уравнением. В отсутствии шумов корр-ый интеграл можен принимать лишь два значения:

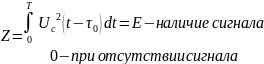, вероятность ложной тревоги =0.

При наличие шума корр-ый интеграл становится случайной величиной. Поэтому вероятность пропуска цели и ложной тревоги принимает некоторое конечное значение. Они определяют отношение энергии сигнала к спектральной плотности шума. Для подсчета этих вероятностей необходимо знать закон распределения корр-го интеграла.

Корр-ый интеграл подчиняется нормальному закону распределения, т.к. представляет собой линейное преобразование нормального случайного процесса. Следовательно, определение подлежит математическому ожиданию и дисперсия корр-го интеграла.

Определим среднее значение (м. о.) при наличии сигнала:

,

- ,

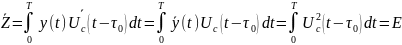Дисперсия корр-го интеграла с точность до постоянного множителя равна дисперсии флуктуации на входе СФ.

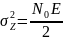, где Е-энергия сигнала.

Заметим, что дисперсия всегда определяется этим выражением вне зависимости от того, присутствует или отсутствует полезный сигнал.

Плотность вероятности нормальной случайной величины при наличии сигнала определяется:

,

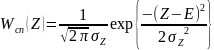при наличии только помехи .

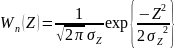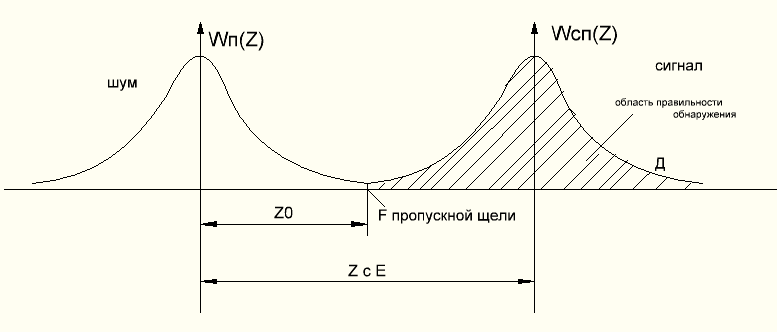
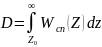– область правильного обнаружения,

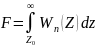– ложная тревога,

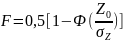- интеграл вероятности.

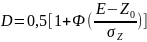- вероятность правильного обнаружения.

Таким образом, вероятность ложной тревоги определяется отношением порогового уровня 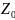к эффективному значению флуктуации корр-го интеграла.

D – зависит от отношения энергии к флуктуации корр-го интеграла. Это отношение совпадает с отношением сигнал-помеха на выходе фильтра. Величина q – параметр обнаружения.

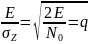, введем обозначение .

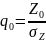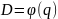- при постоянном F и 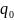будем называть характеристиками обнаружения.

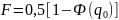
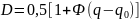
Нарисуем семейство характеристик обнаружения:

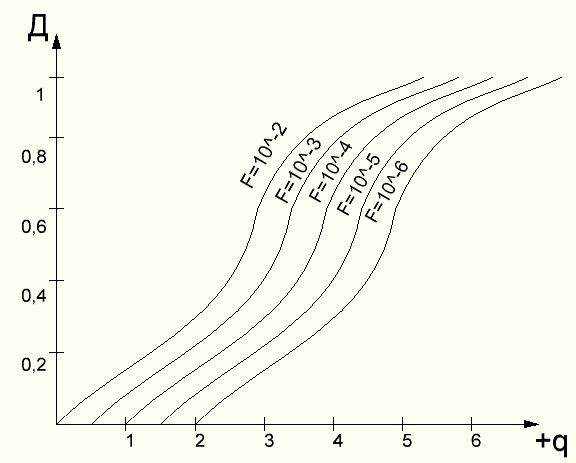
Характеристики обнаружения позволяют найти минимальную энергию сигнала необходимую для обнаружения при фиксированном значении F.

Определив по кривым значение минимума соответственно заданным Д и F, находим минимальную энергию сигнала обеспечивая заданную надежность обнаружения.

,

.

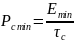Качественный показатель оптимального приемника обнаружения м/б найдены из характеристик обнаружения для сигнала с известными параметрами определяется только энергия сигнала и не зависит от формы.

Тема №6 "Сигнал со случайной начальной фазой"

Если все параметры сигнала известны и начальная фаза тоже, функция правдоподобия записывается следующим образом:

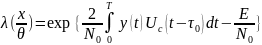
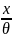- Отношение правдоподобия вычисляется для определенного значения начальной фазы радиоимпульса.

Рассматривается сигнал с неизвестной начальной фазой: (3)

Начальная фаза может принимать любые значения [0,2π]. Т.к. при обнаружении подлежит там факт наличия или отсутствия сигнала в не зависимости от значения начальной фазы. В этом случае отношение правдоподобие может быть вычислено как среднее по всем возможным значениям начальной фазы: 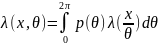, где p(θ) – априорное распределение начальной фазы. Т.к. фаза изменяется от [0,2π], то: .

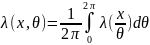Теперь подставляем все и находим отношение правдоподобия с начальной случайной фазой:

.

Следовательно, корреляционный интеграл записывается:

,

,

, , .

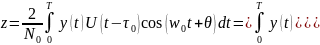
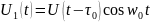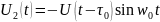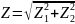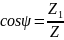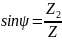Учитывая все предыдущие записи, запишем корреляционный интеграл:

.

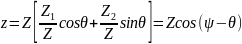Т.к. энергия сигнала практически не зависит от начальной фазы, поэтому записываем, что она равняется Е:

.

Учитывая это, отношение правдопобия примет вид:

.

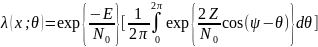В квадратных скобках указана модифицированная функция Бесселя первого рода нулевого порядка аргумента .

Учитывая функцию Бесселя, получим: .

Находим Z: .

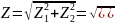Структурная схема.

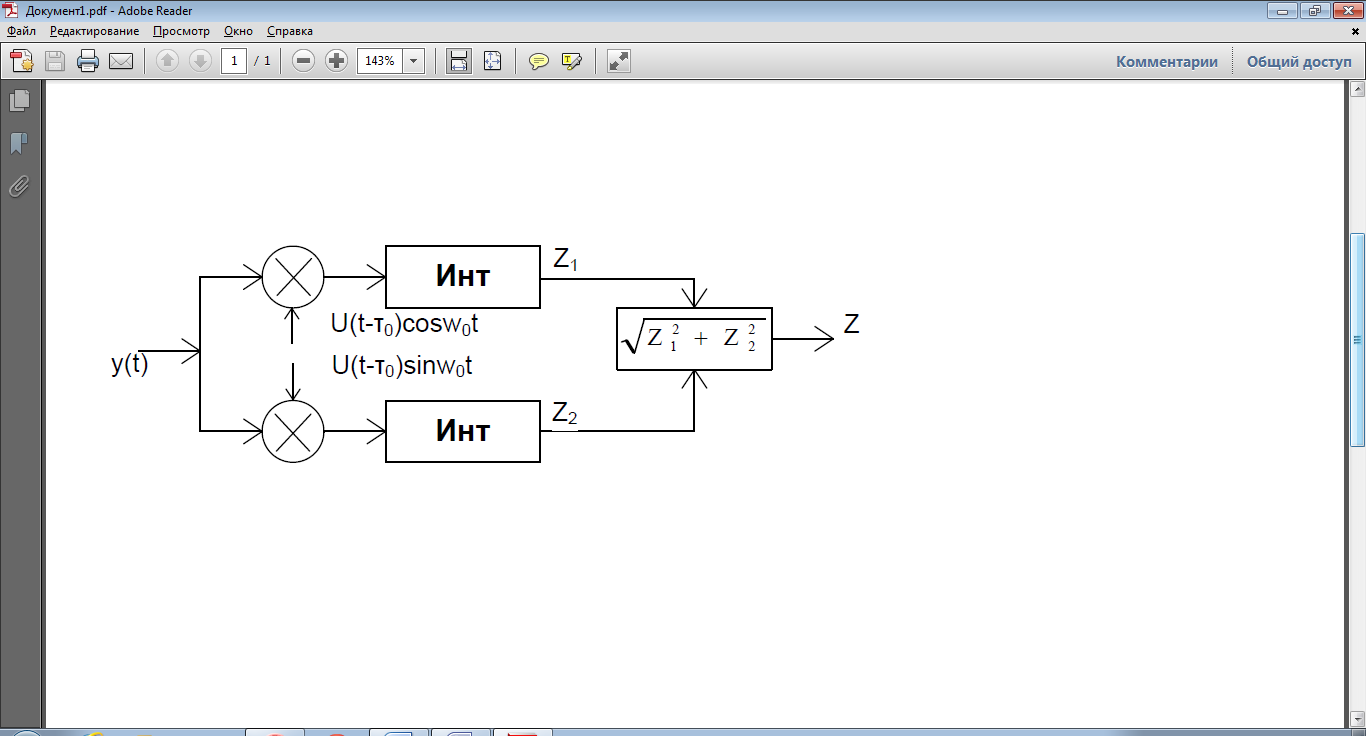
Принятая реализация y(t) поступает на два параллельных канала sin и cos. Каждый канал содержит умножитель и интеграл. В качестве опорных напряжений умножителя, использованы сдвинутые на 90 градусов относительно друг друга радиоимпульсы (sin и cos). Огибающая каждая из них идентична огибающая ожидаемого сигнала. После интегрирования результатом перемножения образуется величины z1 и z2. Вычислительное устройство возводит в квадрат, суммирует и извлекает квадратный корень, на выходе получаем корреляционный интеграл. Далее сравниваем с пороговым значением и принимаем решение: если Z превышает пороговое значение z0, то принимается решение, что сигнал есть, если меньше – сигнала нет.

Рассматриваемый способ обработки сигнала называется корреляционным приемом с двумя квадратурными каналами (sin и cos). Наличие двух квадратурных каналов исключает возможность пропуска сигнала за счет незнания начальной фазы. Если на выходе одного канала фаза равна нулю, то другой даст нам единицу.