СТ РТС

Зябиров Али Хайдарович

Тема №1: «Обнаружение сигналов».

Первая задача заключается в установлении наличии сигнала в принятом колебании. Принятое колебание представляет собой либо смесь полезного сигнала с помехами либо одни помехи. Поэтому прежде чем принять решение нужно провести анализ принятого колебания, которое должно дать возможность отличить наблюдателю полезный сигнал от помех.

Для успешного решения задачи обнаружения наблюдатель должен заранее располагать некоторыми сведениями о полезном сигнале и помехах и использовать эти сведения при обнаружении сигнала. Вот эти априорные сведения дают возможность в совокупности различий между сигналом и помехой факт наличия или отсутствия полезного сигнала. Поэтому оптимальная система правил может быть устранена для сигналов и помех структура, которой той или иной степени определена заранее.

Таким образом, располагая априорными сведениями о полезном сигнале и помехах можно найти правило обработки принятого колебания оптимальные с точки зрения требований предъявляемых к качеству обнаружений.

Установление структуры и потенциальных возможностей устройства оптимальной обработки сигнала является первой частью задачи обнаружения. В качестве помехи мы будем рассматривать нормальный (белый) шум с равномерным в широкой полосе частотным спектром.

Тема №2: «Прием сигналов как статистическая задача».

Задачу приема можно определить как воспроизведение одного сообщения из множества всех возможных. С т.з. получателя посланное сообщение носит случайный характер. Т.к. получателю неизвестно какое именно из множествава всех возможных сообщений получено. Поэтому до приема сообщения получатель может приписать каждому из возможных сообщений априорную вероятность его появления.

Сообщение передается по средству сигнала, которая так же носит случайный характер. Это проявляется в флуктуациях амплитуды и начальной фазы. В связи с этим принятый сигнал лишь с некоторой вероятностью может быть поставлен в соответствии с одним из возможных сообщений. Эта вероятность носит название апостериорная. С уменьшением мешающего воздействия помех концентрация апостериорная вероятности будут возрастать. Если помехи равны нулю, то ап. вер. для какого то сообщения будут равны 1 при 100%.

Принятие решения на основе анализа этой вероятности

Т.О. прием сигналов представляет собой статистическую задачу решение, которого разбивается на два последовательных этапа.

1. Вычисление ап. вер.

2. Принятие решения задачи на основе анализа этого распределения.

Тема №3 «Функция правдоподобия».

В общем случае на вход приемника поступает смесь y(t)=ϕ[U_x(t), U_n(t)], где U_x(t) –сигнал несущего сообщения, U_n(t) –помеха. Задачей приема является воспроизведение сообщения х на основе анализа колебания y(t).

1 этап обработки колебаний: вырабатывается ап.вер. для каждого из сообщений х.

Если х – дискретно – распределение вероятности, если х – непрерывно – плотность распределения вероятности U_x(t). Взаимное соответствие между переданным сигналом и принятым колебанием y(t) определяется их совместным распр. вер-ти W(x,y).

W(x,y)=W(x)W_x(y)=W(y)W_y(x), где W(x) – априорное распр. вер-ти сообщения х, W_x(y) – условное распределение вер-ти значения у при известном х, W_y(x) - условное распределение вер-ти значения х при известном у.

W_y(x)=1/(W(y))*W(x)*W_x(y).

W_y(x)=KW(x)W_x(y)

Поскольку реализация y(t) задана, поэтому W(y)=К некоторая постоянная величина. Т.О. для определения апост. распр-ия достаточно найти W_x(y). В такой постановке это распр-е W_x(y) будет называться функция правдоподобия.

Итог. При заданном априорном распределение вер-ти вычисление сводится к нахождению функции правдоподобия.

Пример.

y(t_i)=[U_x(t_i), U_Ш(t_i)] – аддитивная смесь

W_x[y(t)]=W_Ш[U_Ш(t_i)]= W_Ш[y(t_i)- U_Ш(t_i)].

U_Ш(t_i) - Шум нормальный стационарный. Существует сигнал в течении периода Т сообщения x_j.

Мн-во сообщений х₁, х₂,…,х_m. Каждому сообщению соответствует сигнал х. Все параметры которые заранее известны. Будем считать, что спектральная плотность шума – равномерна от 0 до F_верх. И равняется нулю все этого интервала.

Воспользуемся теоремой Котельникова, разложим шум в интервале времени от 0 до t по ортонормированным функциям:

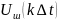, – значение функции в разный момент времени,

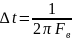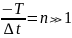, – число точки отсчета, .

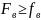Каждой точке отсчета при заданном х функция U_x(t) известна точно. Вероятность того что функция у примет значение равное вер-ти того, что шум в рассматриваемой точке примет значение шума от t (см. пример выше).

Т.к. у нас шум стационарен и нормален для любой точки отсчета, записываем это распределение:

,

.

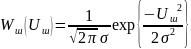Как известно, корреляционная функция шума, спектральная плотность которого N₀равномерна и ограничена с частотой F_в и равняется:

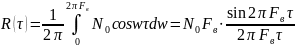
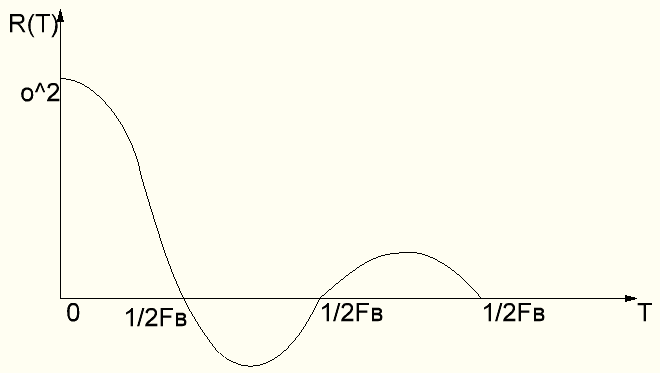
(Рис.1)

Корреляционная функция в точках отсчета равняется нулю, т.е. некоррелированные между собой. Следовательно, при вычислении функции подобия можно рассматривать отсчеты как независимые между собой случ. величины. В каждом случае условная вер-тьW_x(y) равна произведению условных вероятностей для всех рассматриваемых точек отсчета:

.

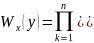Вследствие теоремы Котельникова перепишем предыдущее выражение:

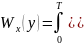dt.

Выражение для функции правдоподобия примет следующий вид:

.

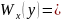Т.о. получая сигнал мы должны его рассчитать.

Интеграл показательной степени принимает минимальное значение при таком U_x(t), которое наилучшим образом совпадет с рассматриваемой реализацией y(t) на всём интервале. Именно при этом значении функция правдоподобия имеет максимум. Указанное значение U_x(t) является наиболее вероятным из всех возможных для данной реализации y(t).

Таким образом, эта функция характеризует степень соответствия между y(t) и всеми возможными U_x(t), а её максимальное значение соответствует наиболее правдоподобной оценке принятого сообщения.

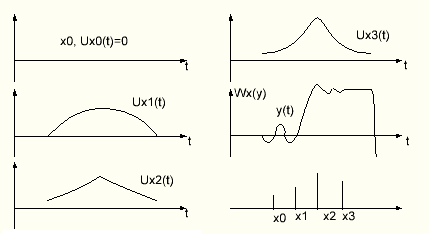
Если х изменяется непрерывно, то функция правдоподобия тоже будет непрерывной.

Анализ функции правдоподобия:

Первый интеграл не интересен, так как в нём только y(t) и никак не связан с информацией, которую несет U_x(t). Численно он равен энергии принятого колебания. Последний - вообще не представляет операцию над принятой реализацией (не представляет интереса). Единственная операция над принятой реализацией y(t),отражающая связь сигнала U_x(t) является вычисление этого интеграла (Z) для всех значений X:

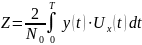- корреляционный интеграл.

Z называют корреляционным интегралом, так как он является мерой взаимной корреляции между реализацией y(t) и всеми возможными сигналами U_x(t). Если эти сигналы имеют одинаковую энергию, то наибольшее значение Zбудет соответствовать сигналу, взаимная корреляция которого с принятым сигналом максимальна.

Располагая значениями корреляционного интеграла для всех возможных сообщений Х можно построить функцию правдоподобия без повторного обращения к реализации y(t). Единственное преобразование, которому должна быть подвергнута реализация y(t) заключается в вычислении корреляционного интеграла Z.

Если нужно найти ф-цию правдоподобия в явном виде, то находим 1-й и 3-ий интеграл.