5.5. Метод функций Ляпунова
Для оценки устойчивости автономной динамической системы (5.1) в случае отсутствия t в явном виде в правой ее части при больших возмущениях А.М. Ляпуновым предложен метод, получивший название метода функций Ляпунова. Рассмотрим его суть.
Положение равновесия автономной динамической системы устойчиво в «в большом», если существует непрерывная функция Ляпунова V(x), определенная в фазовом пространстве переменных х, с непрерывными частными производными по переменным и такая, что
1) V(x) является положительной определенной функцией в замкнутой области , включающей начало координат;
2) производная функции Ляпунова dV/dt в силу уравнений автономной динамической системы dx/dt=f(x) знакоотрицательная функция в или тождественно равна нулю.
Примечание 1. Функция многих переменных называется знакопостоянной, если она, кроме нулевых значений, принимает всюду лишь значения одного знака. Знакопостоянная функция называется знакоопределенной, если она обращается в нуль только в начале координат.
Примечание 2. Если в условиях устойчивости «в большом» dV/dt отрицательно определенная функция в , то обеспечивается асимптотическая устойчивость «в большом».
Фактически область, описываемая функцией Ляпунова V, дает некоторую аппроксимацию реальной области притяжения динамической системы.
Графическая
иллюстрация метода функций Ляпунова
для оценки устойчивости "в большом"
динамической системы второго порядка
приведена на рис. 5.7. На верхней части
рисунка представлен разрез функции
Ляпунова вдоль оси
нижней части рисунка, на котором, в свою
очередь, в координатах
показаны
линии равного уровня функции V;
0 – точка устойчивого равновесия, а 1 –
точка неустойчивого равновесия типа
"седло", что видно из топологии
линий равного уровня функции V.
Очевидно,
что область, очерченная линией 2, является
оценкой области притяжения с помощью
функций V.
Линия 3 представляет реальную область
притяжения динамической системы; тем
самым видно отличие оценки области
притяжения с помощью функции V
от реальной области притяжения.
П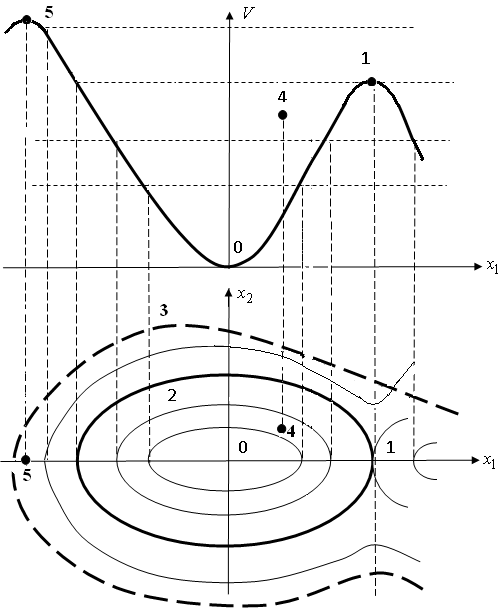
рактически
оно может быть достаточно существенным
и это одна из проблем использования
метода функций Ляпунова, в том числе
применительно к ЭЭС.
П
Рис. 5.7. Иллюстрация метода функций Ляпунова.
роверка устойчивости системы "в большом" обычно заключается в определении координат точек 0 и 1, вычислении значений функции Ляпунова при некотором возмущении (например, в точке 4, которая на рис. 5.7 расположена не в плоскости оси х1) и в точке неустойчивого равновесия 1, а затем – в сравнении этих значений функции V. Если
,
то система устойчива, если
– неустойчива, а
– критический случай.
В классическом виде метод Ляпунова исходит из того, что в начальный момент времени динамическая система находится в возмущенном состоянии (например, в точке 4 на рис. 5.7) и оценивается устойчивость системы "в большом" в предположении свободного ее движения из возмущенного состояния. Свободное движение системы означает изменение ее координат (переменных состояния) при неизменных параметрах. С учетом этого использование метода функций Ляпунова для анализа динамической устойчивости ЭЭС требует решения следующих трех задач:
1) расчет траектории движения ЭЭС во времени до последнего изменения ее параметров, например, численным интегрированием дифференциальных уравнений математической модели динамики системы (см. п. 5.2);
2) конструирование подходящей функции Ляпунова;
3) определение координат устойчивых и неустойчивых положений равновесия системы.
Первая задача не вызывает принципиальных затруднений. От эффективного решения второй и третьей задач зависит, насколько достаточные условия устойчивости, доставляемые методом функций Ляпунова, далеки от необходимых и достаточных. Иначе говоря, насколько оценка области притяжения с помощью функции Ляпунова (кривая 2 на рис. 5.7) далека от действительной области притяжения (кривая 3 на рис. 5.7).
Рассматриваются различные подходы к конструированию функций Ляпунова. Наиболее распространенный основан на использовании первого (энергетического) интеграла консервативной модели динамики ЭЭС (энергетическая функция, функция переходной энергии) в виде:
(5.27)
где первый член в (5.27) представляет кинетическую энергию роторов генераторов, а второй – потенциальную энергию системы. Консервативная модель получается из модели (5.2) при ij=0.
Обращаясь к рис. 5.7, отметим, что кривая на верхней части рисунка представляет потенциальную энергию системы, а величина кинетической энергии определяется скольжением генераторов si в точке возмущенного состояния системы 4.
Известны различные методы определения устойчивых и неустойчивых положений равновесия системы. Все они связаны с решением систем нелинейных алгебраических уравнений. При этом в классическом подходе к использованию метода в качестве критериального значения функции Ляпунова (в точке 1 на рис. 5.7) принималось ее наименьшее значение, достигаемое в одном из неустойчивых положений равновесия. Это часто дает оценки устойчивости ЭЭС, далекие от необходимых и достаточных. Более приемлемые результаты (оценки, более близкие к необходимым и достаточным) дают методы поиска неустойчивого положения равновесия (критериальной седловой точки) в направлении движения ЭЭС.
Проиллюстрируем последнее, несколько упрощая ситуацию, на рис. 5.7. Пусть в точке неустойчивого равновесия 1 значение функции Ляпунова имеет наименьшее значение. Тем не менее, движение системы при конкретном возмущении происходит в направлении точки неустойчивого равновесия 5, в которой критериальное значение функции Ляпунова больше, чем в точке 1. Тем самым мы получим для случая конкретного возмущения оценку устойчивости ЭЭС, более близкую к необходимой и достаточной, т.е. более близкую к границе реальной области притяжения системы.
Трудности конструирования подходящей функции Ляпунова существенно возрастают при использовании метода для детальных математических моделей динамики ЭЭС с учетом, например, АРВ и АРС генераторов. Эти трудности стимулировали разработку так называемых гибридных методов. Предложены два типа гибридных методов.
Основная идея методов первого типа заключается в использовании на первой стадии простых классических моделей ЭЭС типа модели (5.2) или консервативной ее идеализации для предварительной оценки тяжести возмущений. На второй стадии наиболее тяжелые из них исследуются с использованием более детальных моделей методом численного интегрирования системы дифференциальных уравнений динамики ЭЭС.
Гибридные методы второго типа включают следующие стадии:
1) построение функции Ляпунова и критерия динамической устойчивости для простой классической модели динамики ЭЭС в послеаварийном состоянии после последнего изменения параметров системы;
2) численное интегрирование системы дифференциальных уравнений детальной модели до момента вхождения траектории системы в область притяжения, полученную для классической модели ЭЭС.
В целом можно отметить, что за последние десятилетия метод функций Ляпунова применительно к исследованиям динамической устойчивости ЭЭС получил существенное развитие, что позволяет использовать полученные разработки для решения практических задач.