
- •3. Упрощение математических моделей при исследовании устойчивости электроэнергетических систем
- •3.1. Общие положения
- •3.2. Нормативные расчетные условия
- •3.2.1. Исследуемые режимы и возмущения
- •3.2.2. Коэффициенты запаса устойчивости
- •3.2.3. Требования к устойчивости системы
- •3.3. Сокращение расчетных условий с использованием структурного анализа
- •3.4. Преобразование схем замещения ээс
- •3.4.1. Исключение и восстановление узлов
- •3.4.2. Агрегирование и дезагрегирование узлов на основе инверсии метода
- •3.4.3. Агрегирование узлов посредством их объединения
- •3.4.4. Исключение и восстановление связей
- •3.5. Упрощение математического описания системы
- •3.5.1. Показатель влияния возмущения
- •3.5.2. Исследование показателя влияния возмущения
- •3.6. Оценка значимости элементов в системе
- •3.6.1. Показатель структурной связности системы
- •3.6.2. Значимость элемента в системе
- •3.7. Оценка когерентности движения генераторов
- •3.7.1. Уравнение взаимного движения пары машин
- •3.7.2. Показатели когерентности
- •3.7.3. Кластеризация показателей когерентности
- •3.8. Критерии эквивалентирования
- •3.9. Центр инерции. Параметры эквивалента
- •Контрольные вопросы
3.7. Оценка когерентности движения генераторов
3.7.1. Уравнение взаимного движения пары машин
Рассмотрим классическую модель динамики ЭЭС в виде системы дифференциальных уравнений движения генераторов
 (3.28)
(3.28)
где
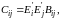 (3.29)
(3.29)
 (3.30)
(3.30)
 активная и реактивная
составляющие взаимной проводимости
сокращенной сети;
активная и реактивная
составляющие взаимной проводимости
сокращенной сети;
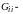 собственная активная проводимость
сокращенной сети.
собственная активная проводимость
сокращенной сети.
Введем обозначения
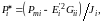 (3.31)
(3.31)
где
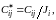 (3.32)
(3.32)
 (3.33)
(3.33)
Рассмотрим уравнение взаимного движения генераторов i и j, для чего из преобразованного с учетом обозначений (3.31)-(3.33) уравнения вида (3.28) для i вычтем аналогичное уравнение для j. В результате получим
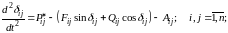 (3.34)
(3.34)
где
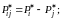 (3.35)
(3.35)
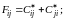 (3.36)
(3.36)
 (3.37)
(3.37)
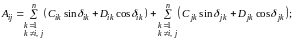 (3.38)
(3.38)
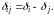 (3.39)
(3.39)
Предполагая, что
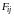 и
и
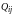 являются составляющими в прямоугольных
координатах некоторой комплексной
величины, имеющей модуль
являются составляющими в прямоугольных
координатах некоторой комплексной
величины, имеющей модуль
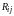 и фазу
и фазу
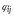 ,
вместо (3.34) получим
,
вместо (3.34) получим
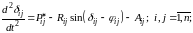 (3.40)
(3.40)
где
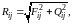 (3.41)
(3.41)
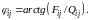 (3.42)
(3.42)
Третий член
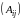 в (3.40) отражает влияние движения остальных
генераторов системы (кроме генераторов
i
и j)
по отношению к рассматриваемым генераторам
i
и j.
Это влияние существенно при большом
значении
в (3.40) отражает влияние движения остальных
генераторов системы (кроме генераторов
i
и j)
по отношению к рассматриваемым генераторам
i
и j.
Это влияние существенно при большом
значении
 ,
сопоставимом с первыми двумя членами
(3.40). При малой (незначительной) величине
взаимное движение генераторов i
и jпрактически
незначительно будет зависеть от движения
генераторов остальной части системы,
этой зависимостью можно пренебречь и
принять
,
сопоставимом с первыми двумя членами
(3.40). При малой (незначительной) величине
взаимное движение генераторов i
и jпрактически
незначительно будет зависеть от движения
генераторов остальной части системы,
этой зависимостью можно пренебречь и
принять
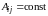 .
Последнее будет в том случае, если
генераторы i
и jмежду
собой сильно связаны, а связи каждого
из них с остальными генераторами слабые,
т.е.
.
Последнее будет в том случае, если
генераторы i
и jмежду
собой сильно связаны, а связи каждого
из них с остальными генераторами слабые,
т.е.
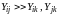 или
или
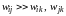 .
В свою очередь, сильная связность
генераторов iиjявляется
необходимым условием их когерентности
(необходимым, но недостаточным, поскольку
когерентность движения генераторов
определяется еще и динамическими
параметрами генераторов и возмущением).
.
В свою очередь, сильная связность
генераторов iиjявляется
необходимым условием их когерентности
(необходимым, но недостаточным, поскольку
когерентность движения генераторов
определяется еще и динамическими
параметрами генераторов и возмущением).
Таким образом, при незначительной величине , принимая , вместо (3.40) получим уравнение взаимного движения генераторов iи jв виде
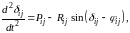 (3.43)
(3.43)
где

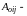 значение
в установившемся доаварийном режиме.
значение
в установившемся доаварийном режиме.
Поскольку (3.43) справедливо при сильной связности генераторов iи jпо сравнению с их связями с остальными генераторами системы и эта ситуация является необходимым условием когерентности генераторов i и j, следовательно, оценки когерентности по уравнению (3.43) будут приемлемыми по точности. В случае же некогерентности генераторов iи j влияние на их движение будет существенным, т.е. допущение неправомочно, а следовательно, сами численные оценки когерентности на основе уравнения (3.43) будут неточными. Однако последнее не имеет значения, поскольку нас интересуют лишь те оценки, которые соответствуют когерентному движению генераторов i и j, а они приемлемы по точности.
